Regularización en R y ejemplo

La regularización en R es una técnica aplicada en la precisión de los modelos de entrenamiento, lo cual influye en que se creen modelos más simples y entendibles sobre un conjunto de datos determinado.

Si el modelo es demasiado complejo, ocurre el sobreajuste, ya que el modelo aprende sobre el ruido de nuestro modelo de entrenamiento y no es capaz de generalizar bien. Para evitar el sobreajuste (overfitting) se puede recurrir a simplificar el modelo o a poner limitaciones sobre el mismo. Esto se conoce con el nombre de regularización en R.

Tipos de regularización en R

• Regularización Lasso o L: permite seleccionar los parámetros que más afectan al resultado. Se añade la función de coste:

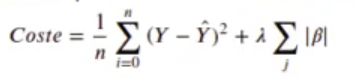
• Regularización Ridge o L²: se evita que los parámetros crezcan demasiado. Se añade la función de coste:

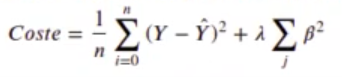
• Elástica: una solución de compromiso entre las dos.

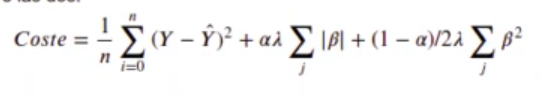
Ejemplo de regularización en R

Vamos a ver un ejemplo de regularización en R por medio de una regresión lineal con tres variables: x0, x1 y x2.

La función que tratamos de modelizar es del tipo:

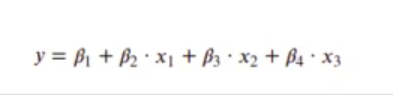
In [1] : #Definimos la función que queremos modelizar en función de beta
myfunction <- function (x_, beta) {beta [1] + x_[ , 1] * beta [2] + x_[ , 2] * beta [3] + x_[ , 3] * beta [4]}

In [2]: beta_real <- c (3, 0.1, -5,4)

set.seed (123)
get_example_data_frame <- function (n =100) {
x1 <- runif (n, min = -10, max = 10)
x2 <- rnorm (n, mean = 7, sd = 9)
x3 <- x1 rnorm (n, mean =3, sd = 2)

df <- data.frame (x1, x2, x3)
df$y = myfunction (df, beta = beta_real) + rnorm (n, mean = 0, sd = 10)
df
}
df <- get_example_data_frame ()
head (df)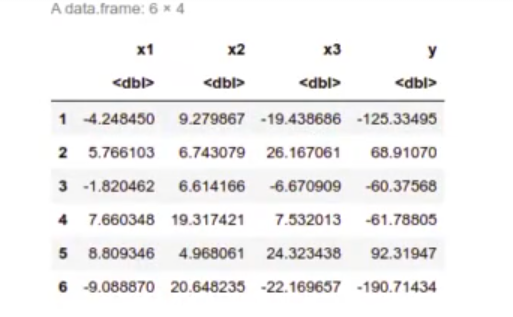

Miramos las correlaciones:

In [3] : cor (df)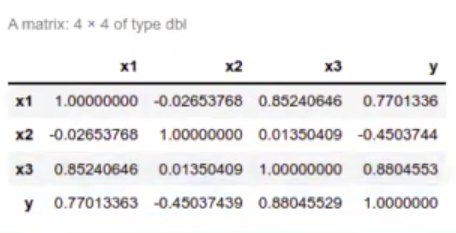

In [4]: library(GGally)
options (repr.plot.height = 4, repr.plot.width = 6, repr.plot.res = 200)
ggpairs (df)

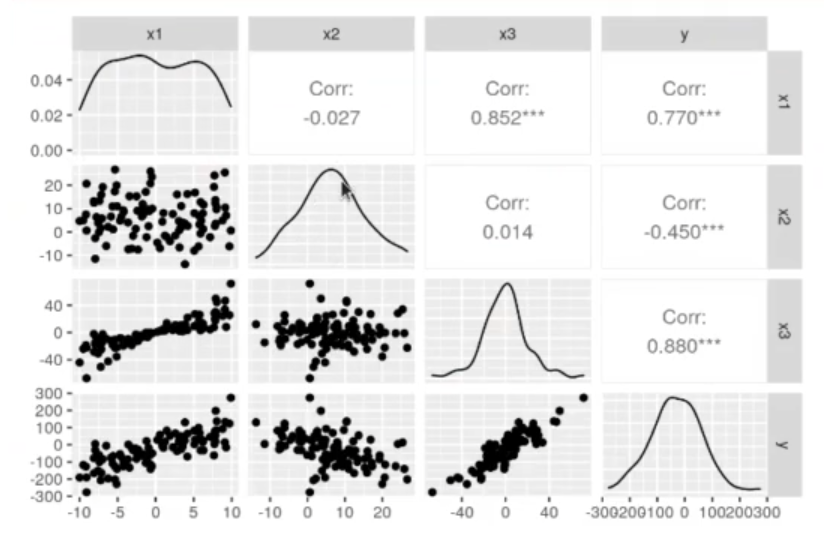
Aquí podemos observar que x1 y x3 están muy correlacionadas, x2 y x3 parece que no.

Si calculamos el modelo:

In [5] : model <- Im (y ~ x1 + x2 + x3, data = df)
summary (model)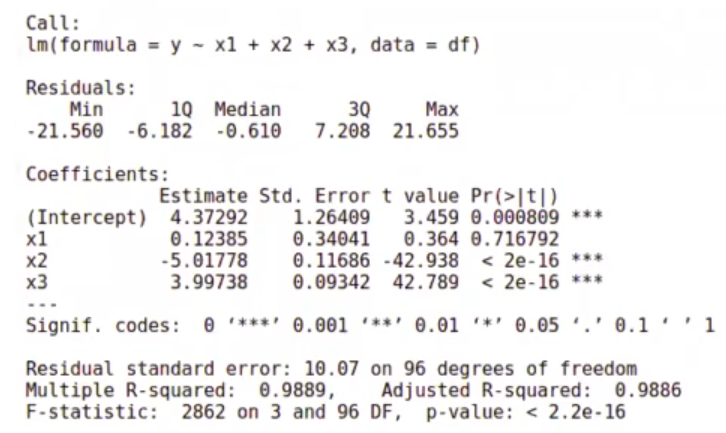

Vemos que depende mucho de x2 y de x3, pero de x1 no parece que dependa.

Siguiendo con el ejercicio de regularización en R, ahora mostraremos los valores de confianza:

In [6] : confint (model)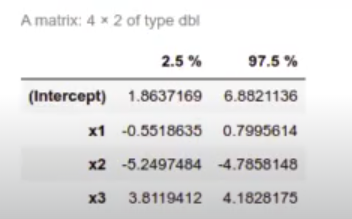

In [7] : #Definimos una función de optimización que nos permite ver cómo evoluciona Beta
optim_beta <- function (mymodel, mse, maxiter-le3, delta = 0.0062, beta_0 = c (0, 0, 0, 0)) {

x_historico <- data.frame (betal = rep (NA, maxiter),
beta2 = rep (NA, maxiter),
beta3 = rep (NA, maxiter),
beta4 = rep (NA, maxiter),
mse = rep (NA, maxiter))
x_historico [1, ] <- c (beta 0, mse (beta 0))

for (i in 2 : maxiter) {
g <- grad (mse, beta_0)
beta_new <- beta_0 - g * delta
beta_0 <- beta_new
x_historico [i, ] <- c (beta 0, mse = mse (beta_0))
}
x_historico <- na.omit (x_historico)
nrow (x_historico)
x_historico$step = 1 :  nrow (x_historico)
x_historico
}

Realizamos una función de optimización. Aquí lo que queremos hacer es minimizar el error cuadrático medio en el proceso de regularización en R:

In [9]: #Definimos la métrica que queremos minimizar, en este caso el error cuadrático medio

mse <- function (beta) {
sum ((df$y - myfunction (df [ , c ('x1', 'x2', 'x3')], beta)) ^ 2) / nrow (df)
}
x_historico <- optim_beta (myfunction, mse, maxiter = 1e4, delta = 0.0005)

In [10] : options (repr.plot.height = 4, repr.plot.width = 8)
g1 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta1), color = 'red') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [1], color = 'black')
g2 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta2), color = 'blue') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [2], color = 'black')
g3 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta3), color = 'green') + theme (axis.text.x element_text (angle = 45)) + geom_hline (yintercept = beta_real [3], color = 'black')
g4 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta4), color = 'orange')+ theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [4], color = 'black')

library (egg)
grid.arrange (g1, g2, g3,g4, nrow = 1)

Tenemos una función llamada mse, que es el minimal squared error. Si nos fijamos bien, esta función son los números reales menos la predicción que puedes hacer.

La predicción se basa en insertar dentro de la función los coeficientes (beta son los coeficientes).

No hemos creado un modelo ni usado el predict, solo estamos llamando la función con los coeficientes beta.

¿Por qué no estamos haciendo esto con las funciones normales? Pues porque lo que queremos es esto:

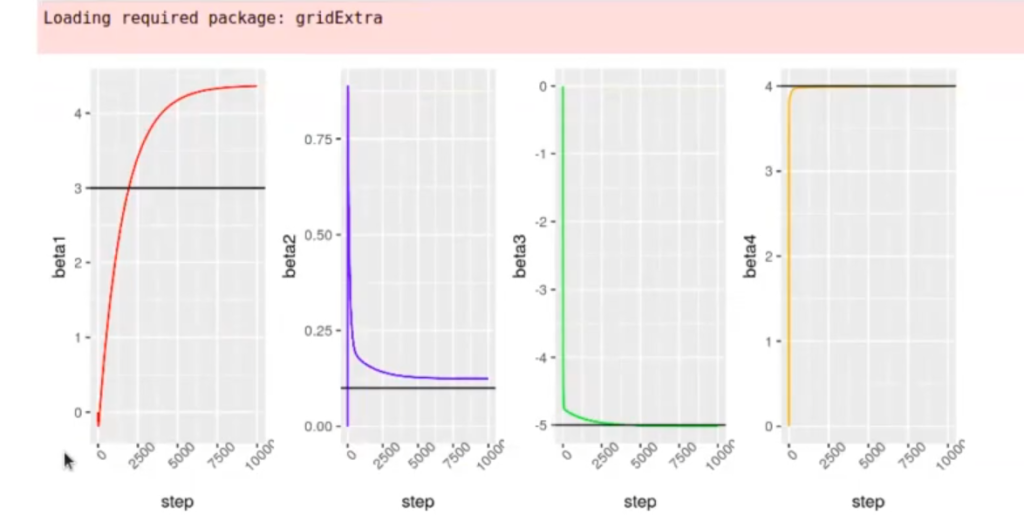
Aquí hemos ejecutado n-iteraciones del algoritmo del descenso de gradientes y hemos monitorizado cómo se comporta cada uno de los betas.

¿Qué sigue?

Ahora que has visto cómo funciona la regularización en R, te queremos invitar a que sigas aprendiendo por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que en pocos meses podrás servirte de los mejores profesionales para impulsar tu carrera o iniciarla. ¡Anímate y solicita más información!