La regularización Ridge en R es bastante similar a la regularización Lasso. Ambas tienen algo en común: introducen un factor de penalización; no obstante, mientras la regularización Lasso toma la magnitud de los coeficientes del modelo, la regularización Ridge en R puede ajustar modelos tomando el cuadrado.
¿En qué consiste la regularización Ridge en R?
Ahora vamos a aplicar una regularización L2 o regularización Ridge en R, añadamos el término:
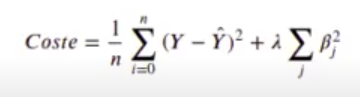
De los coeficientes ẞ, no tenemos en cuenta la intersección. Ten en cuenta que:
- Cuando λ → 0, entonces BRIDGE Boriginalmínimoscuadrados
- Cuando λ → ∞, entonces BRIDGE → 0
Tratamos de minimizar la suma de todos los demás:
In [ ] : lambda <- 10
#lambda <- 1000
loss_ridge <- function (beta) {
mean ((df$y - myfunction (df [ , c ('x1', 'x2', 'x3')], beta)) ^ 2) + lambda * sum (beta (c (2, 3, 4)] ^ 2)
}
x_historico <- optim_beta (myfunction, loss_ridge, maxiter = 1e4, delta = 0.0005)
In [33] : options (repr.plot.height = 4, repr.plot.width = 8)
library (ggplot2)
g1 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta1), color = 'red') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [1], color = 'black')
g2 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta2), color = 'blue') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta_real [2],color = 'black")
g3 <- ggplot (x_historico, aes (x = step)) + geom_line (aes (y = beta3), color = 'green') + theme (axis.text.x = element_text (angle = 45)) + geom_hline (yintercept = beta real [3], color = 'black')
library (egg)
grid.arrange (g1, g2, g3, g4, nrow = 1)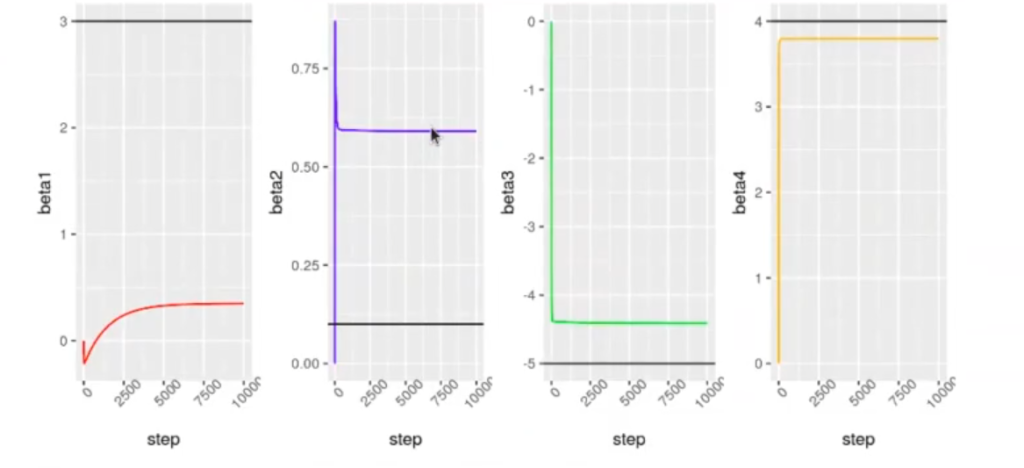
La regularización Ridge en R acerca los coeficientes de las variables más correlacionadas.
También podemos usar el paquete glmnet, en este caso con a=0, ya que utiliza la siguiente función de coste:
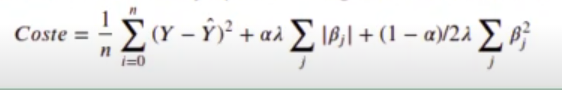
In [34] : library (glmnet)
model <- glmnet (as.matrix (df [ , c ('x1, x2, x3')]), as.matrix (df [, 'y']), lambda = 20, alpha = 0, standardize = F)
coefficients (model)4 x 1 sparse Matrix of class «dgCMatrix»
s0
(Intercept) : 4.271284
x1 : 0.153316
x2 : -5.002668
x3 : 3.988487
In [ ] : fit <- glmnet (as.matrix (df [ , c ('x1, x2, x3)]), as.matrix (df [ , 'y' ]), alpha = 0, standardize = F)
par (mfrow = c (1, 3))
plot (fit, label = TRUE)
plot (fit, label = TRUE, xvar = "lambda")
plot (fit, label = TRUE, xvar = "dev")
grid ()
#print (fit)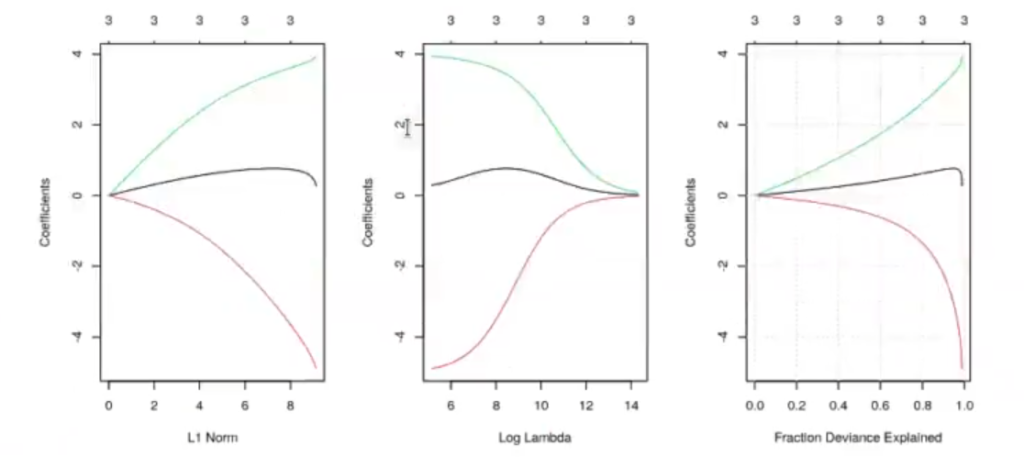
In [36] : cvfit <- cv.glmnet (as.matrix (df [ , c ('x1', 'x2', 'x3')]),
as.matrix (df [ , 'y']),
nfolds = 10, alpha = 0, standardize = F)
plot (cvfit)
Siguiendo con el ejemplo de la regularización Ridge en R, el modelo que tiene un error cuadrático medio más bajo aparece en la variable cvfitSlambda.min.
El modelo que tiene un mayor valor de λ cuya varianza del error está dentro de 1 desviación típica del mínimo aparece en la variable cvfitSlambda. 1se.
Al hacer cross-validation, el MSE no será un valor único, sino que tendremos nfolds diferentes. De todos estos MSE podemos calcular la media y la desviación típica. El valor de lambda. 1 significa que el modelo más sencillo (A más alto) no se diferencia considerablemente del mínimo.
In [37] : cvfit$lambda.min
cvfitslambda.1se170.653343234195
521.150651794727
In [ ] : coef(cvfit, s = "lambda.lse")
In [ ] : cvfit$gimnet.fit$dev.ratio [which (cvfit$glmnet.fit$lambda == cvfit$lambda.Ise)]En resumen, para hacer una predicción Ridge con glmnet haríamos:
In [41] : cvfit <- cv.glmnet (as.matrix (df [ , c ('x1', 'x2', 'x3')]), as.matrix (dfl, 'y']), nfolds = 10, alpha = 0, standardize = F)
cvfit
cvfit$lambda.Ise
In [ ] : df_test <- get_example_data_frame (n = 100)
df_test [ , c ("pred")] <- predict (cvfit, newx = as.matrix (df test [ , c ('x1', 'x2', 'x3')]) , s = cvfit$lambda.Ise)
head (df_test)
caret::postResample (df_test$y, df_test$pred)| x1 | x2 | x3 | y | pred | |
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl [, 1]> | |
| 1 | -2.737908 | 28.393723 | -14.879855 | -205.550223 | -188.330195 |
| 2 | 9.856348 | 7.857318 | 48.472010 | 154.448127 | 157.071228 |
| 3 | 4.514493 | -4.054339 | 9.606328 | 63.954549 | 59.799378 |
| 4 | -7.015591 | 6.995925 | -41.248978 | -203.017480 | -193.015263 |
| 5 | 1.838040 | 8.634610 | 8.515860 | -5.368973 | -4.458573 |
| 6 | 6.974710 | 16.532167 | -3.598633 | -98.342603 | -85.151113 |
RMSE: 10.5959099900708
Rsquared: 0.988084053671031
MAE: 8.27069388317708
Sabemos que al principio cuesta entender esto de la regularización Ridge en R y todos sus ejemplos, sin embargo, es solo cuestión de práctica que te vuelvas un experto en ello y des el siguiente paso en el mundo del Big Data y el data mining.
Recuerda que si quieres seguir aprendiendo sobre la regularización Ridge en R y otras temáticas relacionadas, en Keepcoding tenemos a los mejores profesionales para que te acompañen en tu proceso. Con el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en unos pocos meses aprenderás todo lo necesario para incursionar en un mercado laboral lleno de oportunidades de empleo que te cambiarán la vida. ¡No sigas esperando para solicitar más información y cambia tu futuro ahora!











