¿Sabes qué relación existe entre la transformación lineal y las matrices? ¿Qué es una transformación lineal y qué es una matriz?
Podríamos unir la transformación lineal y las matrices de varias maneras:
- La transformación lineal consiste en multiplicar la matriz por un escalar.
- Es una modificación de matrices por medio de sumas, restas y multiplicaciones, entre otras operaciones aritméticas.
- Es una operación que se hace con los elementos de una matriz, sin alterar la estructura de la misma.
No obstante, la transformación lineal tiene una definición más simple que los puntos que hemos enumerado con anterioridad. A continuación, profundizamos en este tema.
La transformación lineal y las matrices
¿Qué es la transformación lineal?
Para establecer la relación entre la transformación lineal y las matrices, primero habría que definir qué es la transformación lineal.
La transformación lineal no es más que una función. Veamos un ejemplo en el que tenemos una función j (x), le introducimos un dos y sale un ocho (2 → j (x) → 8), le introducimos un siete y sale un quince (7 → j (x) → 15). Esto puede ser una transformación lineal, es decir, una función que recibe un input y nos entrega un output.
Ahora bien, adentrémonos un poco en el tema de las matrices. ¿Qué indica que esta transformación sea lineal?
Podríamos decir varias cosas al respecto, entre ellas:
- Que se mantiene la proporción, una lógica en la estructura, a la hora de cambiar las puntuaciones. Es decir, si introducimos un 2, va a salir un 4; de igual manera, si le introducimos un 4, va a salir un 2.
- Existen dos propiedades matemáticas que se deben cumplir para que sea lineal:
- La función de la suma tiene que ser igual a la suma de las funciones → f (u + v) = f (u) + f (v) ∀u, v ∈ V
- Si F (k . v) = k . F (v) ∀k ∈ R
Condiciones para que una transformación sea lineal
Para que una transformación sea lineal, tendrían que cumplirse dos condiciones. Veámoslas por medio de un ejemplo.
Imaginemos que tenemos un sistema de coordenadas y dibujamos una malla. En el centro del eje, en la posición (0, 0), tenemos el punto de origen. La pregunta que queremos resolver es: ¿qué quiere decir que sea lineal la transformación que tenemos?
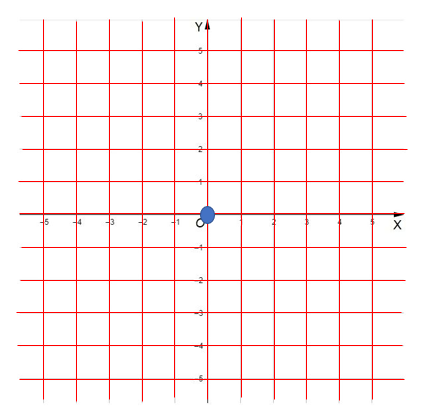
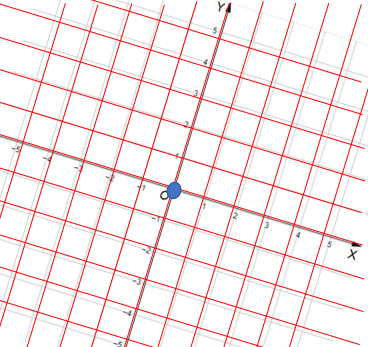
Si le hacemos una transformación a este grid f (x), lo que nos indica es que se deben cumplir dos condiciones:
- Las líneas de la plantilla que seguimos tienen que seguir siendo rectas, es decir, no puede haber distorsión.
- Que el centro u origen se mantiene en la misma posición, es decir, permanece fijo.
Respecto a la primera condición: ¿qué quiere decir que no haya distorsión? Pues que las líneas no pueden ondularse, deben permanecer rectas, tal y como se muestra en la segunda imagen.
Supongamos que nosotros tenemos un eje de coordenadas con un vector v y sus ejes unitarios, que nos están indicando el eje de coordenadas, y aplicamos una transformación lineal:
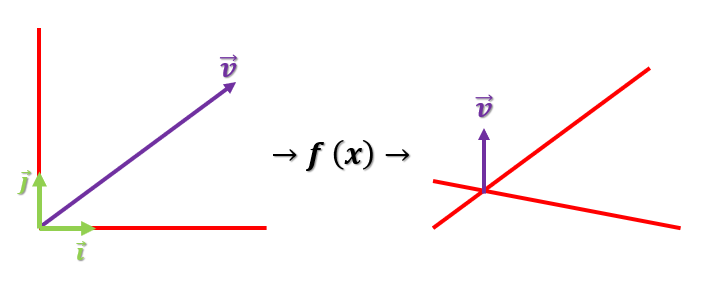
Esta transformación lineal nos indica que el vector está apuntando a un sitio distinto, con los ejes de coordenadas modificados.
¿Qué relación guardan, por tanto, la transformación lineal y las matrices? ¿Para qué nos sirven las matrices? Nos sirven para denotar esta transformación lineal que han sufrido el vector y los ejes de coordenadas, de tal forma que en la matriz asociada estaremos escribiendo dónde acaban los componentes del eje x después de la transformación. Del mismo modo, también escribiremos dónde acaban los componentes del eje y después de la transformación lineal.
Entonces, la matriz nos servirá para representar dicha transformación. De hecho, este es el principal objetivo de las matrices.
Veamos una representación gráfica:
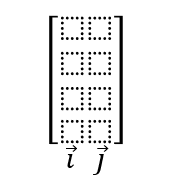
i → Dónde acaban los componentes del eje x.
j → Dónde acaban los componentes del eje y.
Ahora que has aprendido todo lo necesario sobre la transformación lineal y las matrices, puedes seguir formándote en el mundo del Big Data para convertirte en un experto en el sector.
Si quieres acceder a una de las disciplinas más demandadas y con mejores salarios en todo el mercado laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra y de alta intensidad en la que adquirirás, en pocos meses, todos los conocimientos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y atrévete a cambiar tu futuro!



