¿Sabes cómo lidiar con un sistema de ecuaciones sin solución?

Existen dos tipos de sistemas de ecuaciones: los que tienen infinitas soluciones y el sistema de ecuaciones sin solución. Nosotros nos enfocaremos en este segundo, así pues, vamos a intentar resolver un ejercicio para ver qué sucede cuando tenemos un sistema de ecuaciones sin solución.

¿Qué encontrarás en este post?

Sistema de ecuaciones sin solución

Tenemos el siguiente sistema de ecuaciones:

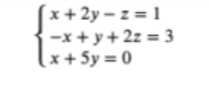
Podemos expresarlo en forma matricial, así:

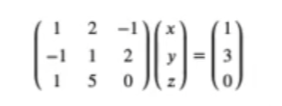
Vamos a usar el mismo proceso que en otros ejercicios para poder encontrar un sistema de ecuaciones similar al inicial:

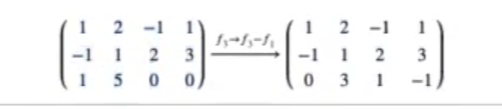
Tenemos, por tanto, un sistema de ecuaciones e intentaremos encontrar un sistema similar al inicial, pero en este caso realizaremos operaciones con las filas. De modo que:

#Sistema de ecuaciones sin solución
imoprt numpy as np
A = np.array ([[1,  2,  -1],
                         [-1,  1,  2],
                         [1,  5,  0]])

B = np.array ([[1],
                         [3],
                         [0]])

AB = np.concatenate ((A,  B), axis = 1)
print (AB)

[[1, 2, -1, 1]

[-1, 1, 2, 3]

[1, 5, 0, 0]]

#Sistema de ecuaciones sin solución
AB = np.array ((AB [0], AB [1], AB [2] - AB [0]))
AB

array (

[[1, 2, -1, 1]

[-1, 1, 2, 3]

[0, 3, 1, -1]])

El siguiente paso que podemos realizar es:

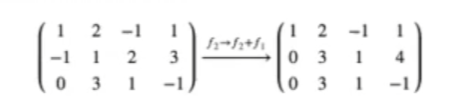
#Sistema de ecuaciones sin solución
AB_ = np.array ((AB [0], AB [1], AB [], AB [2]))
AB_

array (

[[1, 2, -1, 1]

[0, 3, 1, 4]

[0, 3, 1, -1]])

Por último:

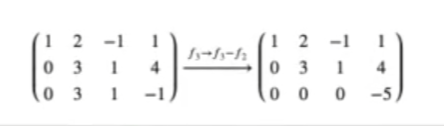
#Sistema de ecuaciones sin solución
AB = np.array  ((AB [0], AB [1], AB [2] - AB [1]))
AB

array (

[[1, 2, -1, 1]

[0, 3, 1, 4]

[0, 0, 0, -5]])

La última fila de la matriz nos indica que algo raro sucede, porque 0 = -5 no tiene sentido. Aun así, vamos a resolverlo usando Sympy:

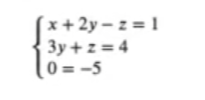
Igualamos a 0:

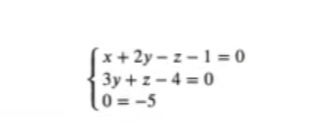
#Sistema de ecuaciones sin solución
from sumpy.solvers import * 
from sympy import *

#Definir las variables que queremos resolver
x = Symbol ('x')
y = Symbol ('y')
z = Symbol ('z')

fun1 = x + 2 * y - z - 1
fun2 = 3 * y + z - 4
fun3 = -5

#Sistema de ecuaciones sin solución
solucion = solve ([fun1, fun2, fun3], [x, y, z])

#Sistema de ecuaciones sin solución
print (solucion)

[ ]

La solución está vacía, lo que indica que este sistema de ecuaciones lineales no tiene solución y, por tanto, es un sistema incompatible.

Resumiendo

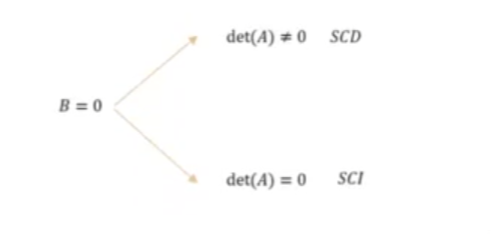
AX = B

Esto es válido para cuando B ≠ 0. No obstante, si en el sistema de ecuaciones B = 0, dicho sistema se denomina sistema homogéneo y son siempre compatibles, es decir, siempre tiene alguna solución. La verdad es que tiene sentido, porque siempre van a admitir la solución trivial de X = 0.

¿Quieres seguir aprendiendo?

Ahora que has aprendido todo lo necesario sobre el sistema de ecuaciones sin solución, puedes seguir formándote en el mundo del Big Data para convertirte en un experto en el mundillo. Para acceder a una de las disciplinas más demandadas y con mejores salarios del mundo laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra en la que adquirirás, en pocos meses, todos los conocimientos que te acercarán al trabajo de tus sueños. ¡Entra ya para pedir información y da el paso que cambiará tu futuro!