Los tensores son una generalización de vectores y matrices y se entienden fácilmente como una matriz multidimensional. A partir de esta definición, podemos extrapolar que:
- Un vector es un tensor unidimensional o de primer orden o tensor de orden 1
- Una matriz es un tensor bidimensional o de segundo orden.
En este post veremos un poco de todo acerca de los tensores, para que así tengas más claridad respecto a este concepto que seguro que ya has visto en el campo del machine learning.
¿Qué son los tensores?
La notacion tensorial es muy parecida a la notación matricial con una letra mayúscula, que representa un tensor, y letras minúsculas con enteros subíndices, que representan valores escalares dentro del tensor.

Muchas de las operaciones que se pueden realizar con escalares, vectores y matrices se pueden reformular para que se realicen con tensores.
Como herramienta, los tensores y el álgebra tensorial se usan ampliamente en los campos de la física y la ingeniería. Al igual que los vectores y matrices, los tensores matemáticas se pueden representar en Python empleando la matriz N – dimensional (ndarray).
Un tensor se puede definir como una lista de listas.
Ejercicios sobre tensores
Veamos algunos ejercicios sobre tensores que pueden sernos de utilidad para comprender a fondo el concepto.
Tenemos un tensor de 3 x 3 x 3 en Python y lo que haremos primero es definir filas; luego, una lista de filas apiladas como columnas; a continuación, una lista de columnas apiladas como niveles en un cubo.
import numpy as np
T = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
print (T.shape)
print (T)(3, 3, 3)
([1 2 3]
[4 5 6]
[7 8 9])
([11 12 13]
[14 15 16]
[17 18 19])
([21 22 23]
[24 25 26]
[27 28 29])
Podemos acceder a sus valores:
T [0]array (
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
T [1]array (
[[11 12 13]
[14 15 16]
[17 18 19]])
T [0] [1].shape(3, )
T [0] [1] [2]6
Operaciones con tensores
Suma
La adición de dos tensores con las mismas dimensiones produce un nuevo tensor con las mismas dimensiones, donde cada valor escalar es la adición de los escalares en los tensores padres.

En numpy podemos agregar tensores directamente al agregar matrices:
A = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])B = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
C = A + B
print (C)
B = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
C = B - A
print (C)
Producto de tensores Hadamard
La multiplicación por elementos de un tensor con otro tensor con las mismas dimensiones da como resultado un nuevo tensor con las mismas dimensiones, donde cada valor escalar es la multiplicación por elementos de los escalares en los tensores padres.
La operación se conoce como oroducto Hadamard, para diferenciarla de la multiplicación tensorial. Aquí utilizaremos el operador o para indicar el funcionamiento del producto Hadamard entre tensores.

A = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
B = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
C = A + B
print (C)
Si cambiamos las dimensiones de uno de los tensores:
A = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
B = np.array ([[[1, 2, 3], [4, 5, 6], [7, 8, 9]],
[[11, 12, 13], [14, 15, 16], [17, 18, 19]],
[[21, 22, 23], [24, 25, 26], [27, 28, 29]]])
print ("A shape: ", A.shape)
print ("B shape: ", B.shape)
print ("C shape: ", C.shape)A shape: (3, 2, 3)
B shape (3, 3, 3)
C shape (3, 3, 3)
C = A * B
C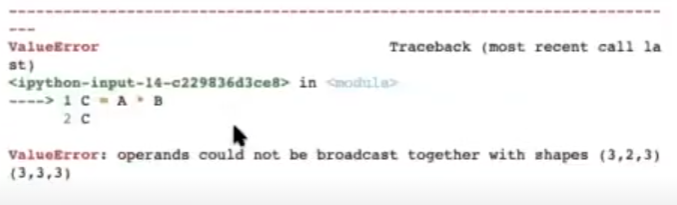
¿Quieres seguir aprendiendo?
Si quieres seguir aprendiendo, podrás acceder a una de las disciplinas más demandadas con la guía del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación en la que adquirirás todos los conocimientos imprescindibles para obtener el trabajo de tus sueños en pocos meses. ¡Entra ya para solicitar información e impulsa tu futuro!











