¿Sabrías cómo calcular el tiempo de espera y la erupción actual de un géiser por medio de las matemáticas? En este artículo te enseñaremos cómo.
El tiempo de espera y la erupción actual
Dentro de este ejercicio tenemos el tiempo de espera y la erupción actual en los ejes x e y. Tenemos, entonces, una gráfica en un eje de coordenadas que representa el tiempo de espera de un géiser cruzado con los datos de lo que dura una erupción actual. Lo que queremos calcular es cuánto tiempo tenemos que esperar para la siguiente erupción. Observemos los siguientes datos en la gráfica:
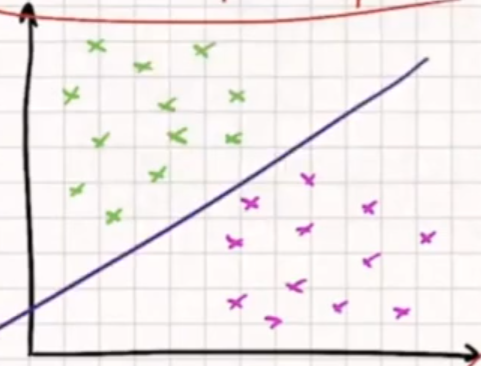
Podemos deducir que los datos son perfectamente separables usando una línea (en este caso, la línea morada del medio). Esta línea o función lineal tiene la forma y = wx + b y será la que nos dictará que, de esta ecuación, aprenderemos los valores de w y de b.
Para aprender los parámetros w y b utilizaremos una función de pérdida, lo que nos llevaría a generar una optimización.
Existen, entre otras, dos formas de optimización: el mínimo cuadrado y el gradiente descendente; estos son dos métodos distintos para resolver este sistema de ecuaciones.
Ejercicio
Ahora veremos un ejercicio que nos ayudará a entender un poco mejor de qué va todo esto de la regresión lineal y el cálculo que intentamos hacer con el tiempo de espera y la erupción actual.
La regresión lineal es el caso más simple de regresión. Imagina que nos hemos ido a Islandia a ver géiseres (geyser) y hemos medido durante un día cada vez que hace erupción y cuánto tiempo dura la erupción. Con estos datos nos gustaría predecir cuándo va a ser la siguiente erupción.
Si observamos los datos, vemos que en el eje x tenemos el tiempo que el géiser estuvo en erupción, y en el eje y tenemos el tiempo que debemos esperar para la próxima erupción. Vemos que, claramente, existe una relación entre ambas variables.
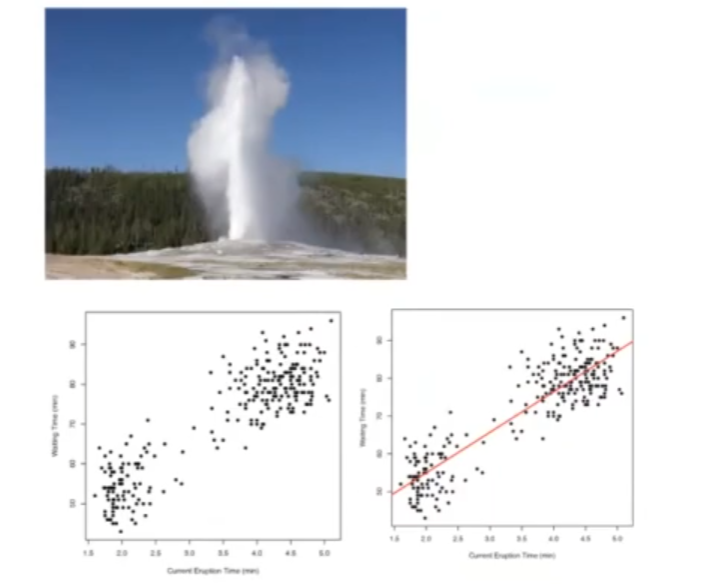
Si miramos estos datos, podríamos querer llegar a algún tipo de función, una simplificación donde simplemente tienes que tomar la entrada, que es el tiempo que el géiser ha estado en erupción. De este modo, la salida será una predicción de cuánto tiempo creemos que vamos a tener que esperar para la próxima erupción. Así, la elección más natural es modelar esto con una función lineal.
Este es el ajuste de regresión más simple, donde tienen una entrada que pensamos que está relacionada de acuerdo a alguna función lineal con la salida.
Vamos, por tanto, a resolver este ejercicio del tiempo de espera y la erupción actual de un géiser con una función lineal.
Función lineal
El modelo para este problema será una función lineal en la que tendremos que la variable y es el tiempo de espera y la variable x es la duración de la erupción.
y = w0 + x . w1
tiempoespera = w0 + duraciónerupción . w1
w1: Pendiente / Slope
w0: Término independiente / Bias / Offset / Shift…
¿Cómo trasladamos esto a problemas con un mayor número de dimensiones?
Imagina que tenemos dos entradas y queremos predecir una salida basada en esas dos entradas. En ese caso, podríamos seguir utilizando una función lineal en la que:
out put = w0 + input1 . w1 + input2 . w2
Geométricamente, podría representarse como:
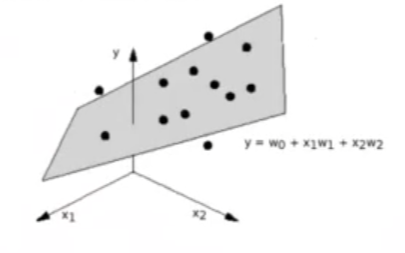
Caso genérico
Por tanto, el objetivo de una regresión es encontrar una función f : Rd→ R, de modo que y ≈ f (x; w) para el conjunto de datos (x, y). Una regresión se denomina lineal si la predicción f es una función lineal con parámetros no conocidos w.
De una forma más genérica podemos escribir la regresión como:
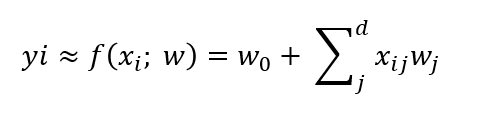
Ten en cuenta que consideramos que tenemos más observaciones que dimensiones d < n.
¿Quieres seguir aprendiendo?
Ahora que sabes cómo resolver el ejercicio sobre el tiempo de espera y la erupción actual de un géiser, puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector. Podrás acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!



