La regresión es un modelo matemático que busca determinar la relación entre una variable dependiente y con respecto a otras variables independientes x. En este artículo te daremos un pequeño resumen sobre las regresiones para que tengas una visión general del tema.
Un resumen sobre las regresiones
¿Qué es la regresión?
La regresión, dado un conjunto de datos, va a predecir una variable continua.
Por tanto, la regresión no es más que un modelo matemático que intenta determinar la relación de una variable dependiente con respecto a otras variables independientes. Es decir, en este caso, queremos predecir el salario respecto a la antigüedad, la educación, etc.
Esa relación viene dada por la siguiente curva:
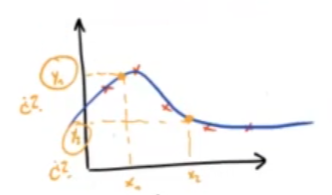
¿Cuál es el objetivo de la regresión?
El objetivo de una regresión es encontrar una función f : Rd tal que y ≈ f (x; w) para el conjunto de datos (x, y). Una regresión se denomina lineal si la predicción / es una función lineal con parámetros no conocidos w.
De forma más genérica, podemos escribir la regresión como:
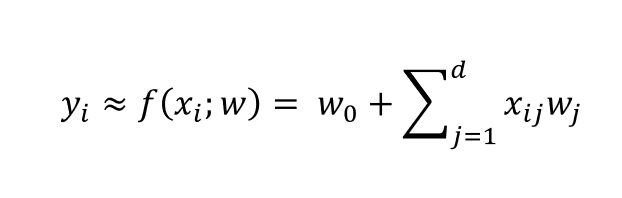
La expresión de la regresión es la que hemos propuesto anteriormente y está íntimamente relacionada con la fórmula de la función de pérdida.
Aquí tenemos w0 y wj y esto va incrementándose a partir del número de columnas que tengamos. Esto es exactamente lo que pasa en el siguiente modelo:
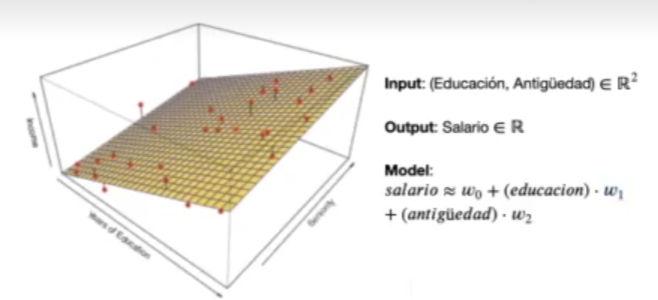
Nota: consideramos que tenemos más observaciones que dimensiones n > d.
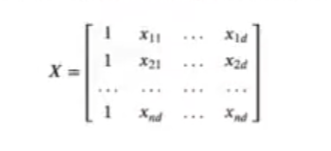
¿Cómo lo resolvemos?
Usando mínimos cuadrados, cuyo objetivo es encontrar los valores de w que minimizan la suma de los errores al cuadrado. Existen distintas formas para la ecuación:
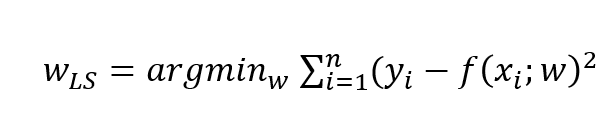
Si desarrollamos la fórmula, podemos llegar a la ecuación de mínimos cuadrados en forma matricial:
XT XW’ = XT y
Así pues, resolvemos el problema de la regresión con la fórmula anterior. Como queremos calcular los parámetros, despejamos W primero.
O lo que es lo mismo:
W’ = (XT X)-1 XT y
Así obtendríamos los parámetros del modelo.
Regresión polinomial
Para casos en los que no podamos modelar nuestro problema con una función lineal, podemos aplicar un polinomio. En este caso se llamaría regresión polinomial y se resuelve de la siguiente forma:
XT XW’ = XT y
W’ = (XT X)-1 XT y
Matriz X
La única diferencia entre la regresión lineal y la regresión polinomial es cómo escribimos la matriz X. Aquí algunos ejemplos:
- Problema con dos dimensiones: en este caso tenemos que aprender el w0 y el w1.
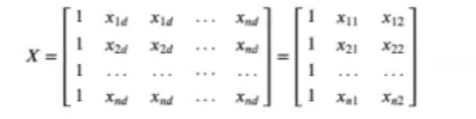
Tenemos, pues, una columna y otra columna. Los valores de x11, x12, x21, x22, xn1, xn2, etc. serían reemplazados con valores de números reales, ya que estos son nuestros datos, lo que conocemos.
- Problemas con tres dimensiones y cuatro observaciones: fijémonos en que tenemos cuatro filas y tres columnas, que vendrían siendo las observaciones.
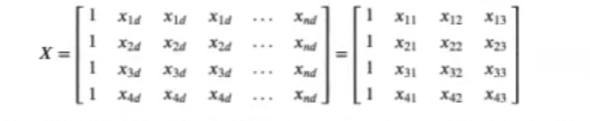
- Problema con cuatro observaciones y dos dimensiones, modelado con un polinomio de segundo grado: es igual que en el caso anterior, pero usando un polinomio de segundo grado. A un polinomio de segundo grado le metemos la primera dimensión y la segunda dimensión; posteriormente, le metemos la primera dimensión al cuadrado y la segunda dimensión al cuadrado.

Todas las matrices tienen una columna llena de unos (1), que es por el w0.
Lo más importante de todo esto es esta fórmula: W’ = (XT X)-1 XT y, que es lo que hace falta para obtener los parámetros de cualquier problema de regresión.
¿Quieres seguir avanzando en tu formación profesional?
El Big Data es una de las áreas en las que más trabajos se ofertan. Para poder acceder a este tipo de opciones laborales, unas de las más prolíficas y mejor pagadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán obtener el trabajo de tus sueños en pocos meses.
Recuerda que en todo momento tendrás el acompañamiento de los mejores profesionales que podrán resolver todas tus inquietudes y te guiarán en el cumplimiento de tus objetivos y metas.
¡No esperes más para impulsar tu carrera y solicita información ahora!











