¿Qué es la varianza en estadística Big Data?

La varianza en estadística Big Data es una herramienta de análisis fundamental y, una vez te familiarices con ella, te resultará muy sencillo comprender cómo llevar a cabo la gestión de un estudio estadístico para los macrodatos.

En este post, te explicamos qué es la varianza en estadística Big Data.

¿Qué es la varianza en estadística Big Data?

La varianza de un estimador nos dice cómo de fiable es nuestro estimador o el margen de error que puede tener. Cuantas menos muestras tengamos, mayor varianza tendrá el estimador.

Por ejemplo:

En la Segunda Guerra Mundial, los alemanes llegaron a conquistar una gran parte de Europa; para derrotarlos, los Aliados tenían que conocer la fuerza de su oponente.

¿Cuántos tanques Panzer fabricaban los alemanes?

Los Aliados se hacían esa pregunta y trataron de obtener respuesta utilizando dos métodos diferentes.

• Métodos convencionales de inteligencia: mediante espionaje tratar de averiguar la capacidad productora.
• Análisis estadístico: analizando los números de serie de diferentes piezas de tanques destruidos en el campo de batalla.

Tras finalizar la guerra se pudieron acceder a los registros alemanes y se vio que el análisis estadístico dio valores muy próximos a los reales:

¿Cómo se estimó?
Partiendo de las siguientes suposiciones:

• Los alemanes ponen número de serie consecutivos a los tanques que fabrican.
• El número de serie empieza en 1.
• Tenemos los números de serie de diferentes tanques destruidos, que son una muestra aleatoria de la población total de tanques.

Consiste en estimar el máximo de una distribución uniforme.

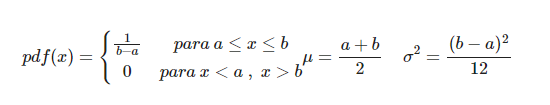
Esta técnica no solo se utilizó para el ejemplo que has visto de los tanques, también se puede utilizar en la actualidad para calcular cual es la producción de cualquier producto. Así, por ejemplo, estas técnicas se pueden utilizar para saber el número de iPhones vendidos.

Ejemplo:
Imaginemos que los alemanes fabricaron en total 5000 tanques, con números de serie del 1 al 5000. Tendremos a=1, y querremos estimar b, cuyo valor real será 5000.

Los números de serie capturados consisten en un muestreo aleatorio simple de la población total de tanques. El objetivo es, sabiendo que se distribuyen siguiendo una función uniforme, estimar el máximo, que llamaremos b, suponiendo que a=1.

Estimación utilizando la varianza

Utilizando el mismo razonamiento que antes, podemos utilizar la varianza para calcular el máximo número de tanques. Sabemos que la varianza de la población total de tanques
tiene que coincidir con la varianza de los números de serie capturados.

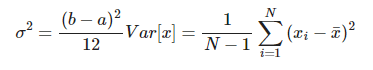
Desarrollando llega la fórmula:

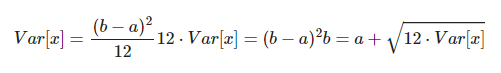
a <- 1
b <- a + sqrt(12*var(capturedSerialNo))
print(paste("Utilizando como estimador la varianza, el número máximo de tanques fabricados es",round(b)))

Estimador insesgado de varianza mínima

Un estimador insesgado de varianza mínima es aquel que tiene menor varianza que cualquier otro estimador insesgado para todos los posibles valores del parámetro. Un estimador insesgado es un estimador que no tiene sesgo, es decir, con sesgo 0. Para el caso de una distribución uniforme es:

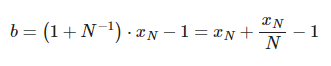
Esta fórmula sale de suponer que:

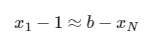
mvue<-rep(NA,numTries)
for (i in 1:numTries){
    capturedSerialNo<-sample(totalPopulationSerialNo,size = numCapturedTanks)
    mvue[i]<-max(capturedSerialNo)*(1+1/length(capturedSerialNo))-1
}
df<-data.frame(mean=meanEstimated,var=varEstimated,mvue=mvue)

ggplot(data=melt(df),aes(x=value,color=variable))+geom_density()+
 scale_color_discrete("Tipo de estimador")+xlab("Número tanques estimados")

margin_mean<-round(quantile(df$mean,c(0.05,0.95)))
margin_var<-round(quantile(df$var,c(0.05,0.95)))
margin_mvue<-round(quantile(df$mvue,c(0.05,0.95)))

print(paste0("Estimador usando la media:    media: ",round(mean(df$mean)),"  varianza: ",round(var(df$mean)),
      "  margen: [",margin_mean[1],",",margin_mean[2],"]"))
print(paste0("Estimador usando la varianza: media: ",round(mean(df$var)),"  varianza: ",round(var(df$var)),
      "  margen: [",margin_var[1],",",margin_var[2],"]"))
print(paste0("Estimador usando la mvue:     media: ",round(mean(df$mvue)),"  varianza: ",round(var(df$mvue)),
      "   margen: [",margin_mvue[1],",",margin_mvue[2],"]"))

Varianza como estimador sesgado

La varianza de una variable muestreada es un estimador sesgado. Para ello, debes tener en cuenta que la varianza se definía como:

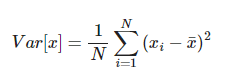
Ahora bien, para comprobar si esto es cierto, puedes suponer que se tiene una distribución uniforme con media cero (0) y varianza cuatro (4). De manera que, si tomas una población de cinco elementos, ¿cuál es la varianza típica?

Para ello, debes repetir este experimento 10.000 veces para comprobar su resultado, de la siguiente manera se produce su inscripción en la consola:

#r <- rnorm(n, mean=0,sd=2)
#r
#myVar(r)

options(repr.plot.height=5,repr.plot.width=8 , repr.plot.res = 400)
set.seed(1)

myVar<-function(X){
    v<-0
    m<-mean(X)
    for (xi in X){
        v<-v+(xi-m)^2
    }
    v/length(X)
}

n<-5

varianzaEstimada<-c()
for (i in 1:10000){
    r <- rnorm(n, mean=0,sd=2)
    varianzaEstimada<-c(varianzaEstimada,myVar(r))
}
print(paste("La varianza esperada es:",mean(varianzaEstimada)))

hist(varianzaEstimada)

Como verás, obtendrás una varianza cercana a 3.242, cuando se sabe que la varianza es realmente 4. Lo que ocurre es que el estimador de la varianza está sesgado, por lo que hay que modificar su fórmula multiplicándolo por el número de elementos de la población de muestra. En este caso sería N=5, así que:

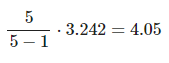
Este es un valor mucho más próximo al esperado. Así pues, hay que reescribir la fórmula de la varianza de la siguiente forma:

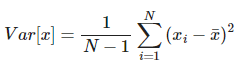
Esta es la fórmula que utiliza R para la función var().

En este post, te has podido relacionar con cómo se implementa la varianza en estadística Big Data. Recuerda que podrás encontrar esta herramienta desde distintas formas, según el interés del estudio estadístico. Además, ¡todavía quedan más tipos de varianza para estudiar!

Por ello, desde KeepCoding te presentamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Por medio del mismo, podrás aprender más sobre la suite de Talend Open Studio junto a las demás herramientas Big Data a través de módulos como Big Data Architecture. Allí, verás una imagen completa del proceso de carga, clasificación, resguardo, gestión y presentación de los datos a través de diferentes herramientas, sistemas y lenguajes. Además, podrás instruirte tanto de manera teórica como práctica ¡No esperes más y apúntate ya!