Aplicar PCA al dataset de proteínas

En el ejemplo de hoy vamos a aplicar PCA al dataset de proteínas, con el que ya hemos trabajado anteriormente.

Recordemos que el PCA o análisis de componentes principales es una técnica estadística de aprendizaje no supervisado utilizada en machine learning para, entre otras cosas, reducir la dimensionalidad, analizar una matriz de covarianza, hacer un análisis de componentes del dataset original para determinar el número de componentes de un determinado conjunto de datos, etc.

Aplicar PCA al dataset de proteínas

Vamos a aplicar PCA al dataset de proteínas:

#Aplicar PCA al dataset de proteínas
mouse <- read.csv ("data/Data_Cortex Nuclear.csv")
mouse data <- mouse [ , 2 : 78]
for (i in 1 : ncol (mouse_data)) {

mn <- mean (mouse_data [ , 1], na.rm = T)
sd <- sd (mouse _data [ , 1], na.rm = T)
mouse_data [is.na (mouse_data[ , 1]), 1] <- mn

mouse_data [ , 1] <- (mouse_data [ , 1] -mn) / sd
}

dim (mouse_data)

1080 . 77

Tenemos, pues, 77 columnas y 1080 componentes.

#Aplicar PCA al dataset de proteínas
#Utilizamos prcomp para calcular el pca
prmouse_data <- prcomp (mouse_data, center = FALSE, scale = FALSE)
#Comprobamos que los 28 primeros autovalores contienen aproximadamente el 90% de la varianza
plot (cumsum (prmouse_data$sdev ^ 2 / sum (prmouse_data$sdev ^ 2)), main = "Autovalores")
grid()

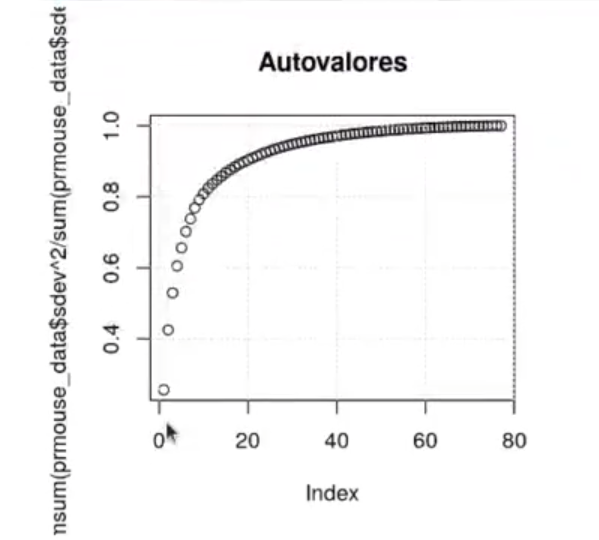
De las 77 muestras, de manera general, podríamos decir que para alcanzar alrededor de un 90% de varianza tenemos que llegar a más o menos 20 autovalores.

Vamos a quedarnos con tres componentes principales y vamos a pintarlos:

#Aplicar PCA al dataset de proteínas
head (mouse)
prmouse_data_pca <- as.data.frame (prmouse_data$x[ , c ("PC1", "PC2", "PC3")])
prmouse_data_pca$cl <- mouse [ , "class"]
prmouse_data_pca$Genotype <- mouse [ , "Genotype"]
prmouse_data_pca$Treatment <- mouse [ , "Treatment"]
library (ggplot2)
ggplot (prmouse_data_pca, aes (x = PC2, y = PC3, color = Treatment)) + geom_point () ggplot (prmouse_data_pca, aes (x = PC1, y = PC2, color = Genotype)) + geom_point ()

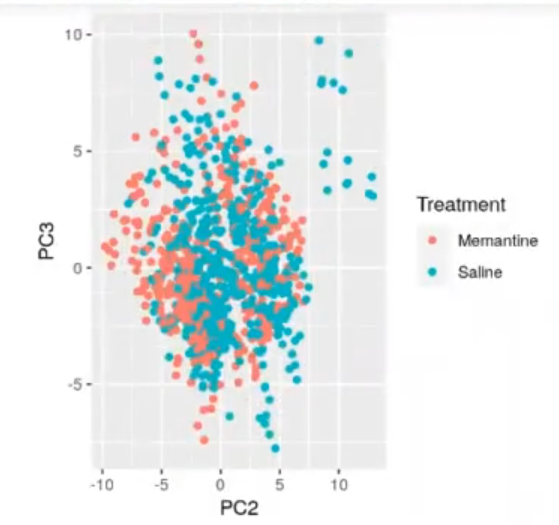
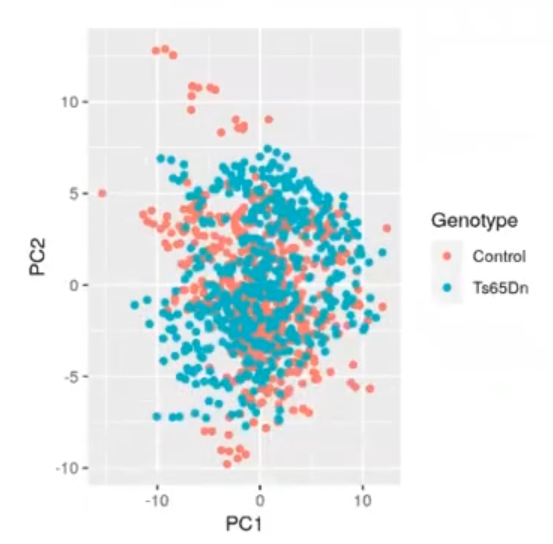
Vamos a probar a hacer un k-means con solo dos dimensiones del PCA:

#Aplicar PCA al dataset de proteínas
mouse_data14 <- prmouse_data$x [ , 1 : 2]
q <- c ()
for (k in 1 : 20) {
myclust <- kmeans (mouse_data14, k)
q [k] <- myclust$betweenss / myclust$totss
}
plot (q)

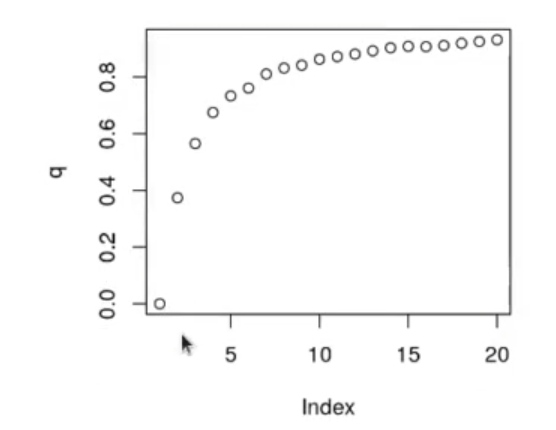
Ahora haremos un clustering a partir de 10 muestras y dos componentes principales:

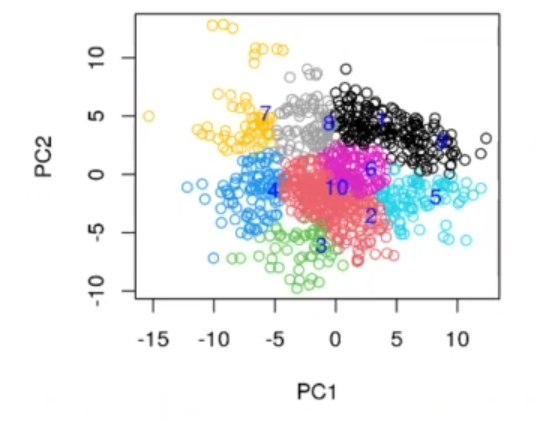
#Aplicar PCA al dataset de proteínas
set.seed (123)
myclustpca <- kmeans (mouse_data14, 10)
myclust <- kmeans (mouse_data, 10)

table (mouse$class, myclustpca$cluster)
table (mouse$class, myclustscluster)
table (mouse$Behavior, myclustpca$cluster)
table (mouse$Behavior, myclust$cluster)

plot (prmouse_data$x [ , c(1, 2)], col = myclustpca$cluster)
text (x = myclustpca$centers [ , 1], y = myclustpca$centers [ , 2], cex = 1, pos = 4, labels = (1 : nrow (myclustpca$centers)), col = "blue")

	1	2	3	4	5	6	7	8	9	10
c-CS-m	11	11	0	13	5	32	19	31	11	17
c-CS-s	22	3	0	4	0	20	26	22	23	15
c-SC-m	0	59	21	2	21	15	0	0	0	32
c-SC-s	0	21	7	11	27	13	0	0	1	55
t-CS-m	40	0	0	0	11	15	9	25	30	5
t-CS-s	33	3	1	0	1	16	6	19	20	6
t-SC-M	0	29	28	30	2	5	0	0	0	41
t-SC-s	0	15	1	31	23	34	1	0	2	28

	1	2	3	4	5	6	7	8	9	10
c-CS-m	43	16	23	5	11	17	11	0	0	24
c-CS-s	24	22	29	0	3	28	0	0	15	14
c-SC-m	0	10	0	31	31	1	70	7	0	0
c-SC-s	12	5	0	10	23	0	70	15	0	0
t-CS-m	12	38	38	0	2	0	0	0	0	45
t-CS-s	11	18	41	3	0	11	0	0	0	21
t-SC-M	10	0	0	34	20	10	48	13	0	0
t-SC-s	26	14	0	8	2	18	5	44	0	18

	1	2	3	4	5	6	7	8	9	10
C / S	106	17	1	17	17	83	60	97	84	43
S / C	0	124	57	74	73	67	1	0	3	156

	1	2	3	4	5	6	7	8	9	10
C / S	90	94	131	8	16	56	11	0	15	104
S / C	48	29	0	83	76	29	193	79	0	18

Una vez abordada esta temática, podemos darnos cuenta de que al aplicar PCA al dataset de proteínas vemos y practicamos muchos conceptos diferentes. Si te gustaría profundizar en ellos, podrás lograrlo por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación intensiva podrás adquirir todos los conocimientos necesarios para convertirte en un gran profesional e incursionar rápidamente en un mercado laboral lleno de oportunidades. ¡Anímate y solicita más información!