En este post vamos a calcular distintas métricas de clasificación a partir de una matriz de confusión. En esta ocasión empezaremos por un modelo de clasificación sencillo, la regresión logística, y posteriormente iremos aumentando la dificultad.
Trabajaremos con un conjunto de datos que contiene los datos de fuga de una compañía de teléfonos. Lo que queremos averiguar es en qué momento las personas cancelan los servicios de telefonía.
Calcular distintas métricas de clasificación
Regresión logística
#Calcular distintas métricas de clasificación: logistic regression
from sklearn.model selection import train_test_split
from sklearn.preprocessing import StandardScaler
#preparamos los datos
columns_to_drop.append ('churn')
X = data [features].values
y = data ['churn'].values
#PASO 1:
X_train, X_test, y_train, y_test = train_test_split (x, y, test_size = 0.25, stratify = y, random_state = 0)
scaler = StandardScaler ().fit (X_train)
Xs_train = scaler.transform (X_train)
Xs_test = scaler.transform (X_test)
print (Datos train: ', Xs_train.shape)
print("Datos test: ', Xs_test.shape)
print ('Proporción train: %0.3f' %np.mean (y_train))
print ('Proporción test: %0.3f %np.mean (y_test))Datos train: (2499, 15)
Datos test: (834, 15)
Proporción train: 0.145
Proporción test: 0.145
Con estos resultados vemos que la proporción se mantiene.
Ahora, ajustaremos un algoritmo de regresión logística sobre el conjunto de entrenamiento con C = 1. Calcularemos la predicción para el conjunto de entrenamiento (y_pred).
#Calcular distintas métricas de clasificación: logistic regression
from sklearn.linear model import LogisticRegression
lr = LogisticRegression (C = 1).fit (Xs_train, y_train)
y_pred_train = lr.predict (xs_train)#Calcular distintas métricas de clasificación: logistic regression
from sklearn.metrics import confusion_matrix
confmat = confusion_matrix (y_train, y_pred_train)
plot_confusion_matrix (confmat)
#Podemos acceder a los valores de la matriz
tn, fp, fn, tp = confusion_matrix (y_train, y_pred_train).ravel ()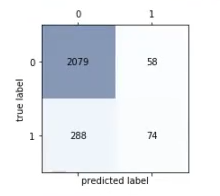
Aquí lo que hemos hecho es predecir sobre train. Este procedimiento sirve para plottear la matriz de confusión.
Lo que vemos en el resultado es que, para la clase negativa, el modelo se comporta muy bien, ya que hay muchos verdaderos negativos; no obstante, observamos que para la clase minoritaria las cosas no funcionan tan bien, porque hay muchos 1 que están clasificados como 0. De hecho, hay muchos más 1 que están clasificados como 0 que 1 correctamente clasificados como 1.
El siguiente paso será, a partir de las métricas TP, TN, FP, FN, calcular las siguientes métricas: SEN, ESP, PPV, FSC, ACC.
#Calcular distintas métricas de clasificación: logistic regression
calcula_metricas (confmat)ACC: 0.8615446178471389
SEN: 0.20441988950276244
ESP: 0.9728591483387927
PPV: 0.5606060606060606
FSC: 0.29959514170040485
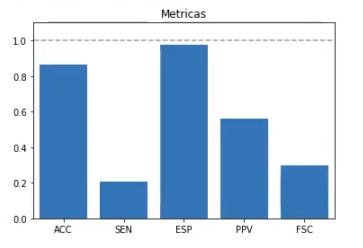
Vemos cómo las métricas que tienen que ver con el valor 2079 son muy altas. Fijémonos, por ejemplo, en la instancia ESP, que está casi al 100.
Ahora veamos cómo están las gráficas que le dan más peso al valor 74: son muy bajas.
Acto seguido, calcularemos las métricas de performance en el conjunto de test:
#Calcular distintas métricas de clasificación: logistic regression
y_pred_test = lr.predict (Xs_test)
confmat = confusion_matrix (y_test, y_pred_test)
calcula_metricas (confmat)ACC: 0.86810551558753
SEN: 0.23140495867768596
ESP: 0.9761570827489481
PPV: 0.6222222222222222
FSC: 0.3373493975903615
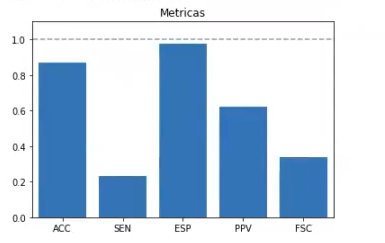
Ambas gráficas no son exactamente iguales, pero sí son muy similares.
Luego, representaremos el histograma de probabilidad estimada y_prob para el conjunto de test. Representaremos de distinto color cada una de las clases:
#Calcular distintas métricas de clasificación: logistic regression
y_prob = lr.predict_proba (Xs_test) [ : , 1]
idx_0 = (y_test == 0)
idx_1 = (y_test == 1)
plt.hist (y_prob [idx_0], density = 0, alpha = 0.75, label = 'y = 0')
plt.hist (y_prob [idx_1], density = 0, facecolor = 'red', alpha = 0.75, label = 'y = 1')
plt.legend ()
plt.title (feature)
plt.show ()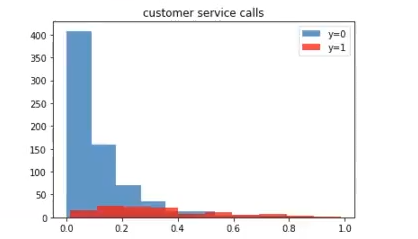
Los no fugados equivalen al número 0; los fugados equivalen al número 1. La mayoría de ceros están clasificados de manera correcta. Hay algunos que tienen menos probabilidad de ser cero, pero en general, podríamos decir que la gráfica está bastante bien distribuida.
Por último, representaremos la curva ROC:
#Calcular distintas métricas de clasificación: logistic regression
from sklearn.metrics import roc_curve, auc
ejex, ejey. = roc_curve (y_test, y_prob)
roc_auc = auc (ejex, ejey)
plt.figure ()
plt.plot (ejex, ejey, color = 'darkorange', lw = 2, label = 'AUC = %0.2f' % roc_auc)
plt.plot ([0, 1], [0, 1], color = (0.6, 0.6, 0.6), linestyle = ' - - ')
plt.plot ([0, 0, 1], [0, 1, 1], lw = 2, linestyle = ' : ', color = 'black', label = 'Clasificador perfecto')
plt.xlim ([-0.05, 1.05])
plt.ylim ([-0.05, 1.05])
plt.xlabel ('FPR (1 - ESP)')
plt.ylabel ('SEN')
plt.legend (loc = "lower right")
plt.show ()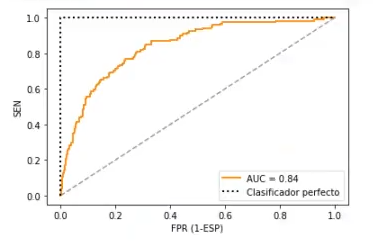
El Big Data es una de las áreas en la que más trabajos se ofertan. Si quieres ser uno de los afortunados que puede acceder a este tipo de opciones laborales bien pagadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán obtener el trabajo de tus sueños. ¡No esperes más para seguir tu camino hacia el éxito y solicita información ahora!











