La curva ROC se comenzó a usar durante la segunda guerra mundial para el análisis de las señales de radar. Después del ataque a Pearl Harbor en 1941, la armada de EEUU comenzó un programa de investigación para aumentar la predicción de los radares a la hora de detectar aviones japoneses. Para ello, midieron la habilidad de un radar de detectar esas señales y a esa medida la llamaron Receiver Operating Characteristic o curva ROC.

La curva ROC se utiliza para ver la calidad de un detector, un clasificador binario capaz de detectar un elemento. Se hace un barrido por todos los umbrales y se mide el valor de positivo verdadero en función de falso positivo.

Ejercicio curva ROC

En artículos anteriores hemos visto algunos ejercicios acerca de cómo identificar de una serie de datos entrantes, cuáles eran ruido y cuáles eran aviones. Entre otros, hicimos la matriz de confusión de dicho ejercicio y le aplicamos las medidas de calidad respectivas.

En este artículo, realizaremos la curva ROC de esa matriz de confusión. Para ello, pintaremos la probabilidad de true positive y false positive.

In [46] : <- 4
radar_pred <- predict (model, radar.test)

df_preds <- data.frame (pred = radar_pred,
tipo_pred = factor (ifelse (radar_pred < umbral, 0, 1), labels = c ("ruido", "avión")),
tipo_real = radar.test$tipo)
df_preds <- df_preds [order (df_oreds$pred, decreasing = FALSE) , ]

M <- table (df_preds$tipo_real, df_preds$tipo_pred)
#table (real = radar.test$tipo, elegimos = y_est)

#Recall, Exhaustividad, Tasa Verdadero positivo
truePositive <- M [2, 2] / (M [2, 2] + M [2, 1])

#Tasa Falso positivo
falsePositive <- M [1, 2] / (M [1, 2] + M [1, 1])
paste ("tp:", truePositive, "fp:", falsePositive)
M

df_preds

‘tp: 0.363636363636364 fp: 0’

	pred	tipo_pred	tpo_real
	<dbl>	<fct>	<fct>
14	-12.998054	ruido	avión
49	-12.212471	ruido	avión
5	-10.568399	ruido	avión
52	-8.774266	ruido	avión
4	-5.860805	ruido	avión
42	1.181265	ruido	avión
30	1.605634	ruido	avión
10	1.763440	ruido	avión
22	2.499537	ruido	avión
7	2.604227	ruido	avión
27	3.117978	ruido	avión
28	3.730055	ruido	avión
24	3.975999	ruido	avión
51	3.984776	ruido	avión
25	4.711617	ruido	avión
60	6.052678	ruido	avión
35	7.213312	ruido	avión
31	9.375621	ruido	avión

In [47] : calctp_fp <- function (y_predict, y_real, th) {
y_est <- ifelse (y_predict < th, 0, 1)

M <- table (y_real, y_est)
#print (M)
if (ncol (M) == 2 & nrow (M) == 2) {
truePositive <- M [2, 2] / (M [2, 2] + M [2, 1])
falsePositive <- M [1, 2] / (M [1, 2] + M [1, 1]) 
c (tp = truePositive, fp = falsePositive)
} else {
c (tp = NA, fp = NA)
    }
}

In [48] : calctp_fp (df_preds$pred, df_preds$tipo_real, th = -1)

0.285714285714286

In [49] : dfROC <- data.frame (th =unique (df_preds$pred), tp = NA, fp= NA, model = "model1")

#for (th in seq (min (df_preds$pred), max (df_preds$pred), lenght.out = 10)) {
#calctp_fp (df_preds$pred, df_preds$tipo_real, th = th)
# }
for (i in 1 : nrow (dfROC)) {
v <- calctp_fp (df_preds$pred, df_preds$tipo_real, th = dfROC$th [i])
dfROC$tp [i] <- v ["tp"]
dfROC$tp [i] <- v ["fp"]
}
ggplot (data = dfROC, aes (x = fp, y = tp)) + geom_path ()

Warning message:

«Removed 1 row (s) containing missing values (geom_path).»

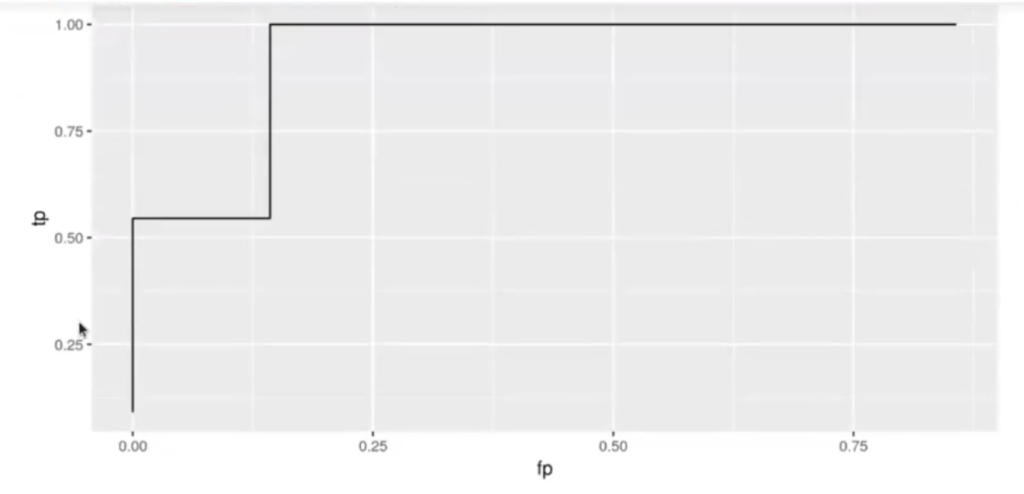
La curva ROC sale tan escalonada porque tenemos pocas muestras. Vamos a probar con un dataset más grande:

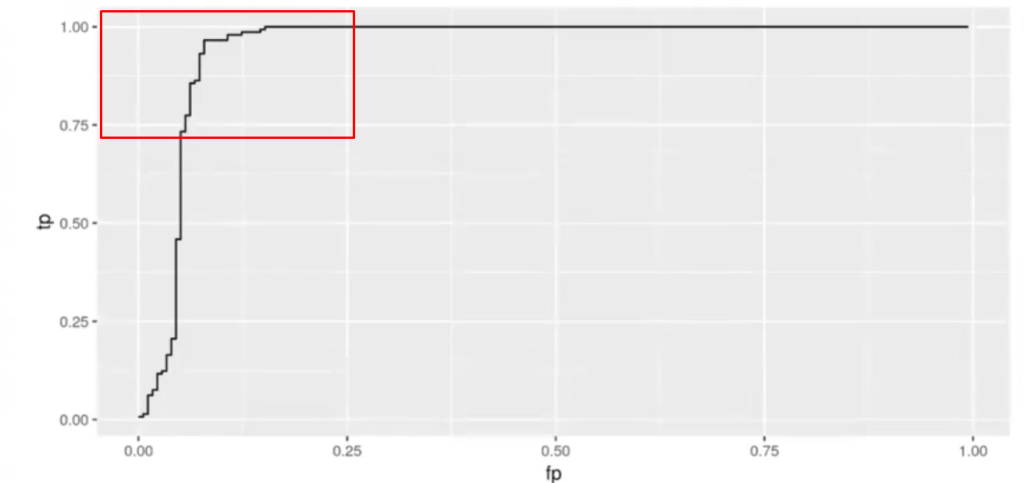
En función de qué clasificador quisiéramos con la curva ROC, nos interesaría más o menos estar por el área señalada en el recuadro rojo.

In [53] : library (ROCR)

#p <- predict (model_radar1, radar_big.test, type = "response")
p <- predict (mode_radar1, radar_big.test)

pr <- prediction (p, radar_big.tests$tipo, label.ordering = c ("ruido", "avion"))
prf <- performance (pr, measure = "tpr", x.measure = "fpr")
plot (prf, colorize = TRUE)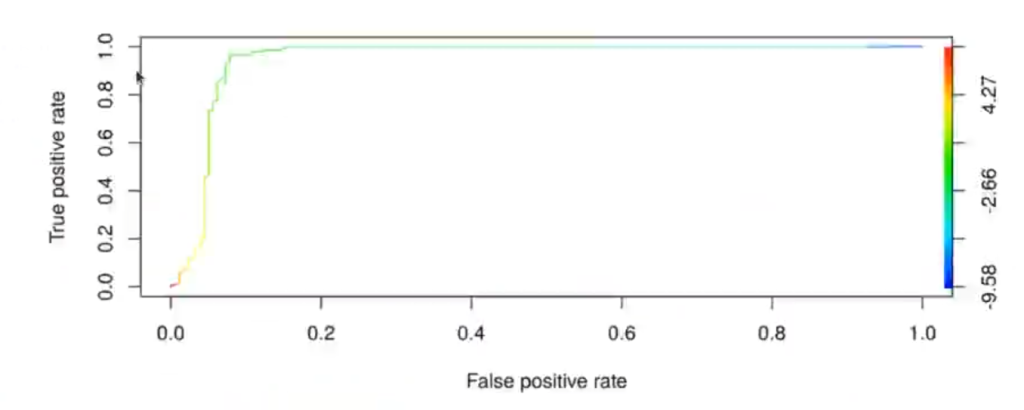

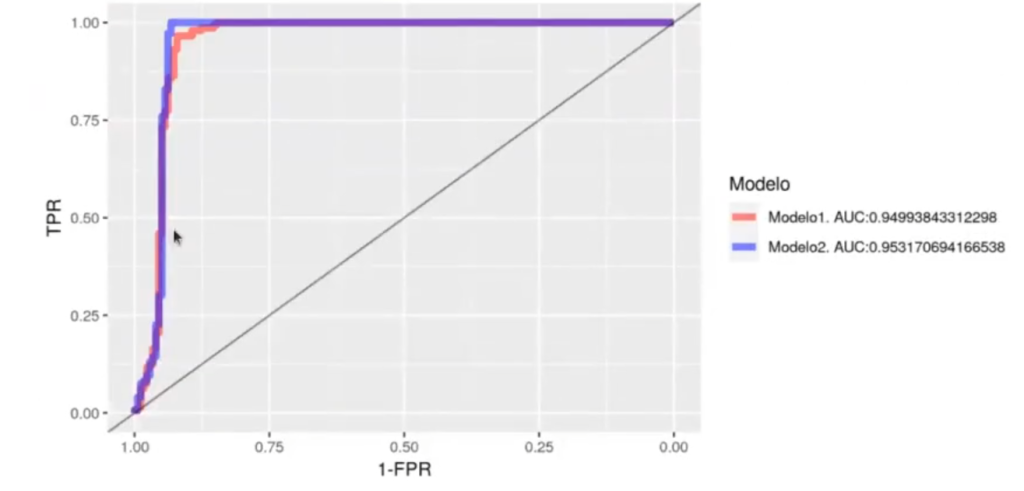
In [62] : pauc2 <- performance (pr2, measure = "auc", label.ordering = c ("ruido", "avión"))
[email protected] [[1]]

0.953170694166538

In (63): #library(pROC)
rocobjl <- PROC::roc(
radar_big.test$tipo,
predict (model_radar1, radar_big.test))

rocobj2 <- PROC::roc (
radar_big.test$tipo,
predict (model_radar2, radar_big.test),
levels = c ("ruido", "avion"), direction = "<")

#plot (rocobjl, print.auc = TRUE, col = "blue")
#plot(rocob)2, print.auc = TRUE, col = "green", print.auc.y = .4, add = TRUE)

pROC :: ggroc (list (model1 = rocobj1, model2 = rocob12), alpha = 0.5, size = 2) + xlab ("1 ~ FPR") + ylab ("TPR") + geom_abline (slope = 1, intercept = 1, alpha = 0.5)+
scale_colour_manual (values = c ("red", "#0000FF"), name = "Modelo", labels = c (paste0 ("Modelo1, AUC: " , PROC :: auc (rocobj1)),
paste0 ("Modelo2, AUC, PROC :: auc (rocobj2))))

Setting Levels: control = ruido, case = avion

Setting direction: controls < cases

Ya hemos visto qué es la curva ROC, cuál es su origen y cómo funciona, ¿ahora qué te parece si seguimos aprendiendo sobre estadística, Big Data y data mining? Para ello, desde Keepcoding te ofrecemos nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el cual en muy poco tiempo dominarás todos los conocimientos necesarios para convertirte en un gran científico de datos y acceder a las mejores ofertas laborales del mercado. ¡Anímate a impulsar tu carrera y solicita más información!

¿Qué es la curva ROC?

Ejercicio curva ROC