Ejemplo: capas ocultas de las neuronas en Deep Learning

En el desarrollo de este post, te compartimos un ejemplo relacionado con las capas ocultas de las neuronas en Deep Learning, también conocidas como hidden layers. De esta manera, podrás practicar y conocer en profundidad cómo funciona este tipo de análisis para el manejo de los macrodatos.

Capas ocultas de las neuronas en Deep Learning

Para nuestro ejemplo sobre las hidden layers o capas ocultas de las neuronas en Deep Learning, como primer paso vamos a hacer las importaciones:

%tensorflow_version 1.x

TensorFlow 1.x selected.

# Imports necesarios
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

# Importamos el dataset MNIST y cargamos los datos
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

Si todo ha ido bien, el perceptrón simple con TensorFlow será capaz de reconocer con una precisión en torno al 92% dígitos del 0 al 9 escritos a mano. A continuación, incluimos una primera hidden layer de 200 neuronas al perceptrón simple que hemos desarrollado en el ejercicio anterior para descubrir el efecto de dar profundidad a nuestra red creando ya un multilayer perceptron.

Para ello, en este ejemplo con capas ocultas de las neuronas en Deep Learning, habrá que definir las variables (W1, B1) y (W2, B2) en TensorFlow y recalcular las predicciones: Y^=softmax(Y1∗W2+B2) siendo Y1=sigmoid(X∗W1+B1).

Ten en cuenta que, conforme le damos profundidad a la red, es importante inicializar los pesos (W1 y W2 en nuestro caso) con valores aleatorios siguiendo una distribución gaussiana. De otra forma, el optimizador puede quedarse atascado en la posición inicial y no ser capaz de moverse en la dirección del mínimo de la función de pérdidas.

Por ello, utilizaremos la función de TensorFlow tf.truncated_normal, tal y como se indica en la documentación de TF. Además, vamos a aprovechar este ejercicio para convertir nuestro código dejado en un script a una función cuya cabecera será la siguiente:

Nota: copia y pega el código anterior en una nueva celda y conviértelo en función. Posteriormente, añade la segunda capa oculta.

1. Tras la modificación, se debe ejecutar la función train_shallow_net con sus parámetros de entrada tomando el valor del apartado anterior. ¿Qué sucede? No se percibe la influencia de hacer la red más profunda, puesto que el número de épocas es pequeño para ello.
2. Ahora, lanza de nuevo el entrenamiento de nuestra shallow net, pero con un valor de n_epochs = 1000. ¿Qué sucede? Ahora sí se aprecia la mejora, concretamente obtenemos una precisión en torno al 97% sin overfitting, esto último es importantísimo.

Nota: la última ejecución tardará unos 20 minutos, por lo que puedes aprovechar para leer detenidamente el siguiente apartado.

def train_shallow_net(learning_rate, batch_size, num_epochs):
  # Creamos placeholders para ir almacenando los datos de entrada y los labels
  X = tf.placeholder(tf.float32, [None, 784]) #(X) # Imágenes del mnist: 28*28 = 784
  Y_true = tf.placeholder(tf.float32, [None, 10]) #(X) # Número indicando la clase 0-9 => 10 clases

  # Creamos e inicializamos las variables W y b con valores aleatorios que sigan una distribución normal
  W1 = tf.Variable(tf.truncated_normal([784, 200], stddev=0.1)) #(X)
  B1 = tf.Variable(tf.zeros([200])) #(X)
  W2 = tf.Variable(tf.truncated_normal([200, 10], stddev=0.1)) #(X)
  B2 = tf.Variable(tf.zeros([10])) #(X)

  # Calculamos las predicciones
  Y1 = tf.nn.sigmoid(tf.matmul(X,W1) + B1) #(X)
  Y_pred = tf.nn.softmax(tf.matmul(Y1,W2) + B2) #(X)

  # Definimos función de pérdidas (Cross_entropy)
  loss = tf.reduce_mean(-tf.reduce_sum(Y_true * tf.log(Y_pred), reduction_indices=1)) #(X)
  #loss = tf.reduce_mean(-tf.reduce_sum(Y_true*tf.log(Y_pred), reduction_indices=1))

  # Optimizador SGD
  train = tf.train.GradientDescentOptimizer(lr).minimize(loss) #(X)

  # % de predicciones correctas en un determinado batch (i.e. accuracy)
  is_correct = tf.equal(tf.argmax(Y_pred,1), tf.argmax(Y_true,1))
  accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
  
  # Inicializamos variables
  init = tf.initializers.global_variables() #(X)

  # Abrimos la sesión
  with tf.Session() as sess:
    sess.run(init) #(X)
    # Entrenamiento de nuestra red
acc_epoch_tr = []
    acc_epoch_val = []
    loss_epoch_tr = []
    loss_epoch_val = []
    for epoch in range(n_epochs):
      avg_acc = 0.
      avg_loss = 0.
      steps = int(mnist.train.num_examples/batch_size) #(X) Calcular número de batches
      for i in range(steps):
        batch_X, batch_Y = mnist.train.next_batch(batch_size) #(X) # Pedir un nuevo batch del set de datos (emplear función next_batch)
        sess.run(train, feed_dict={X: batch_X, Y_true: batch_Y}) #(X) # Entrenamos 
        a,l = sess.run([accuracy, loss], feed_dict={X: batch_X, Y_true: batch_Y}) #(X) # Calculamos accuracy y cross_entropy del batch
        avg_acc += a / steps #(X) Calcular el accuracy medio de los diferentes batches
        avg_loss += l / steps #(X) Calcular las pérdidas medias de los diferentes batches
      # Almacenamos el accuracy y las losses medios para cada época
      acc_epoch_tr.append(avg_acc) #(X)
      loss_epoch_tr.append(avg_loss) #(X)
      # Calculamos accuracy y losses en validation
      a_val, l_val = sess.run([accuracy, loss], feed_dict={X: mnist.validation.images, Y_true: mnist.validation.labels}) #(X)
      acc_epoch_val.append(a_val) #(X)
      loss_epoch_val.append(l_val) #(X)
      # Sacamos información por pantalla
      print("[INFO]: Época {} ---> Acc_train = {} - Loss_train = {} - Acc_val = {} - Loss_val = {}".format(epoch, avg_acc, avg_loss, a_val, l_val)) #(X)

    # Cálculo de accuracy y losses en el conjunto de test
    a_test, l_test = sess.run([accuracy, loss], feed_dict={X: mnist.test.images, Y_true: mnist.test.labels}) #(X)
    print("[INFO]: Accuracy en test = {} - Losses en test = {}".format(a_test, l_test)) #(X)

    # Gráficar losses por época
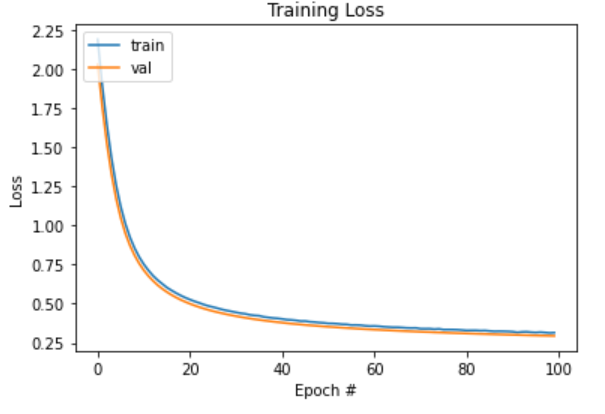
    plt.plot(np.arange(0, n_epochs), loss_epoch_tr) #(X)
    plt.plot(np.arange(0, n_epochs), loss_epoch_val)
    plt.legend(['train', 'val'], loc='upper left')
    plt.title('Training Loss') #(X)
    plt.xlabel('Epoch #') #(X)
    plt.ylabel('Loss') #(X)

# Lanzamos entrenamiento
lr = 0.005
b_size = 128
n_epochs = 100
train_shallow_net(lr, b_size, n_epochs)

Sigue estudiando sobre el Big Data

En este post, te hemos expuesto un breve ejemplo relacionado con las hidden layers o capas ocultas de las neuronas en Deep Learning, de forma que ahora podrás contar con esta práctica. Sin embargo, ¡todavía falta mucho por aprender! Por ello, no dudes en echarle un vistazo a nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, con el que te convertirás en un experto en pocos meses. ¡Pide información e inscríbete ya!