La clasificación estadística de regresión logística para el manejo del Big Data forma parte del desarrollo de una de las etapas más importantes para un estudio estadístico: la clasificación. En efecto, una correcta clasificación le proporcionará a un análisis como la regresión lineal mejores resultados a partir de las variables adecuadas.
Por otra parte, este tipo de ayudas te facilitarán las fórmulas y su asertividad en cuanto aprendas a implementarlas efectivamente. En general, los estadísticos te harán comprender cómo se comportan las variables y las relaciones que se establecen entre ellas. Por ello, en este artículo, te explicamos qué es y cómo funciona la clasificación estadística de regresión logística para el manejo del Big Data.
Clasificación estadística de regresión logística
La clasificación estadística de regresión logística se utiliza si lo que tienes en tu procesamiento de los datos son dos grupos y quisieras realizar una clasificación. Entonces, tendrás que realizar ciertas modificaciones a la regresión lineal, es decir, el modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente Y, la variable independiente X y un término aleatorio ε.
Por lo tanto, primero te recordamos que la fórmula de la regresión lineal es:
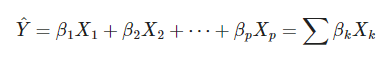
A partir de allí, vas a tratar de asignar una probabilidad a esta población de datos. Entonces, esta será la clasificación estadística de regresión logística.
Por ejemplo
Ahora, para mostrar efectivamente cómo funciona la clasificación estadística de regresión logística, te presentaremos un breve ejemplo:
Vas a partir de que trabajas en una maderera y quieres saber si un tronco es de un abedul o de un abeto basándote únicamente en el diámetro y la longitud del tronco. Entonces, su inscripción se desarrollaría de la siguiente forma:
library(ggplot2)
options(repr.plot.height=3,repr.plot.width=7, repr.plot.res = 300)
arboles<-read.csv("data/arboles.csv", stringsAsFactors = T)
ggplot(arboles,aes(x=diametro,y=longitud,color=especie))+geom_point(size=0.3)
En este caso, apuntará a un gráfico de dispersión como el siguiente, en el que el color azul determina el abeto y el rojo el abedul a partir de las variables longitud (Y) y diámetro (X):
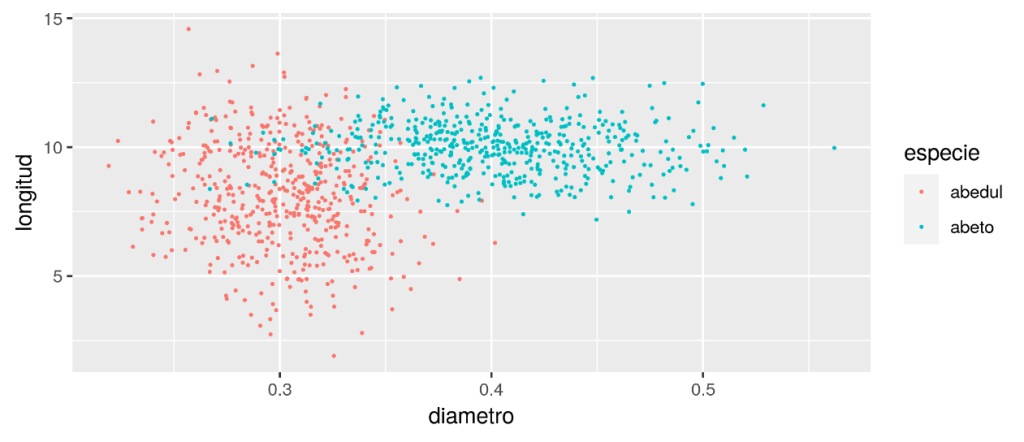
Posteriormente, podrás hacer una clasificación con un modelo lineal donde crees una nueva columna especie.n y le asignes:
- abeto = 1
- abedul = -1
A partir de allí, utilizas un modelo lineal tal que:
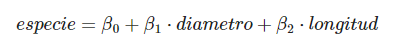
Entonces, la clasificación estadística de regresión logística seguirá así:
- Si especie >= 0 es un abeto.
- Si especie < 0es un abedul.
La recta que marcará el umbral será:
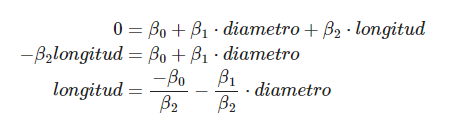
Ahora bien, la inscripción de la clasificación estadística de regresión logística se planteará de la siguiente forma:
arboles$especie.n[arboles$especie=="abeto"] <- 1 arboles$especie.n[arboles$especie=="abedul"]<- -1 itrain<-sample(1:nrow(arboles),round(nrow(arboles)*0.7)) arboles.train<-arboles[itrain,] arboles.test<-arboles[-itrain,] modellm<-lm(data=arboles.train,formula=especie.n~diametro+longitud) beta<-modellm$coefficients beta ggplot(arboles.train,aes(x=diametro,y=longitud,color=especie))+geom_point(size=0.3)+ geom_abline(intercept = -beta[1]/beta[3],slope = -beta[2]/beta[3], color="red" )

A continuación, la gráfica de dispersión contará con la recta de umbral de la clasificación estadística de regresión logística:
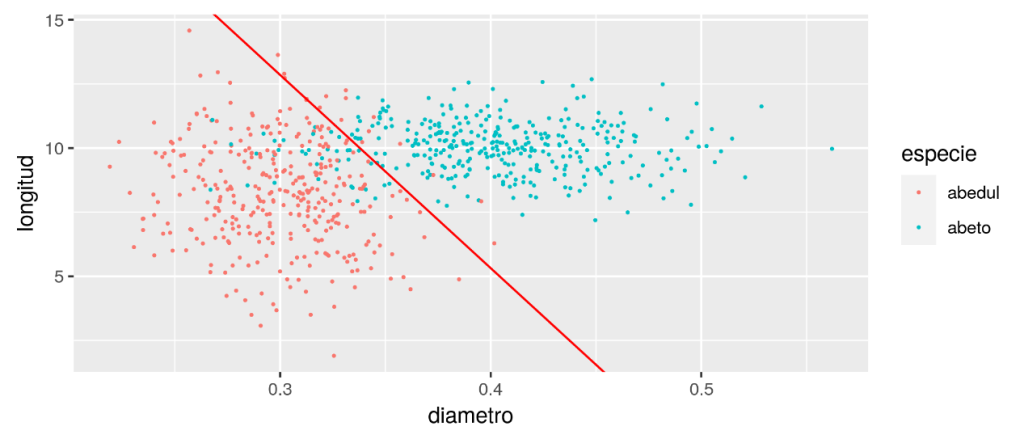
Sin embargo, esto no es del todo correcto, porque los datos NO siguen una distribución gaussiana. Cada iteración, cada línea del dataframe, cada árbol medido, podrían seguir una distribución de bernoulli.
De manera que es un abeto con probabilidad p o es un abedul con probabilidad (1-p). Esto se puede generalizar con una distribución binomial que indique la probabilidad de que n troncos sean abedules.
Para pasar del dominio de números reales en la clasificación estadística de regresión logística (−∞,∞) al de probabilidades [0,1], vas a utilizar la función logística:
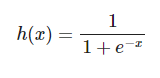
Su inversa se conoce como la función logit:
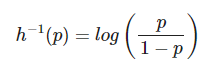
x<-seq(-10,10,length.out = 100) y<-1/(1+exp(-x)) plot(x,y,t="l")
Esto, en la gráfica, se vería de la siguiente manera:
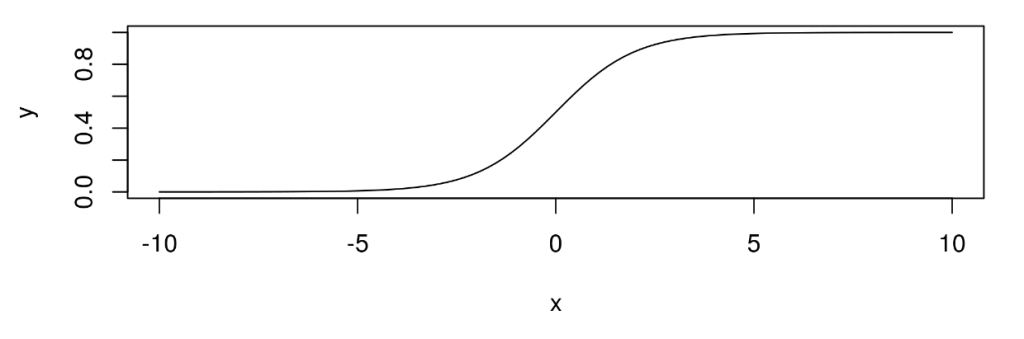
Es decir, tendrías una probabilidad porque su valor está en el rango [0,1]:
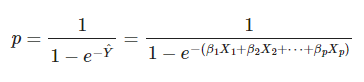
A partir de allí, vas a definir la razón de monomios (Odds ratio) como el cociente entre dos probabilidades, ya que su valor está en el rango [0,∞]:
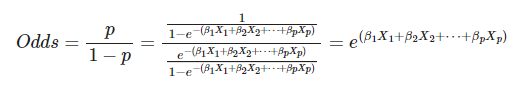
Ahora, si aplicas el logaritmo a la razón de monomios, tendrás un valor que está en el rango [−∞,∞]:
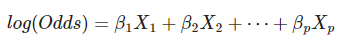
Por último, podrás repetir el ejercicio de antes poniendo el umbral en 0 igualmente, pero con regresión logística:
table(as.factor(arboles.train$especie))
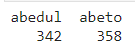
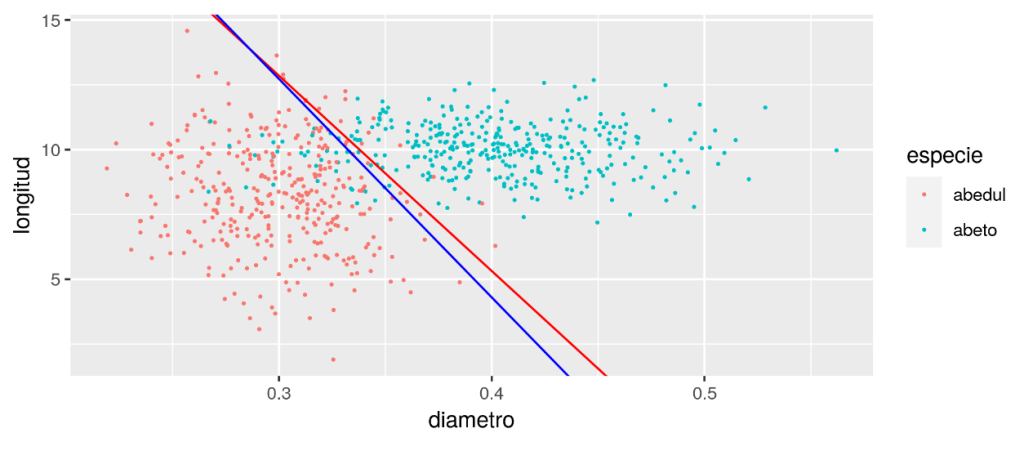
model<-glm(data=arboles.train,formula=especie~diametro+longitud,family=binomial(link='logit')) betalg<-model$coefficients ggplot(arboles.train,aes(x=diametro,y=longitud,color=especie))+geom_point(size=0.3)+ geom_abline(intercept = -beta[1]/beta[3],slope = -beta[2]/beta[3], color="red" ) + geom_abline(intercept = -betalg[1]/betalg[3],slope = -betalg[2]/betalg[3], color="blue" )
En definitiva, los cálculos juntos apuntarían a la siguiente gráfica con las mismas variables, sin embargo, el cambio de umbral a 0 produciría otra línea:
Por medio de este post, te hemos explicado qué es y cómo funciona la clasificación estadística de regresión logística para el manejo del Big Data; sin embargo, su desarrollo requiere de una práctica constante. Por este motivo, te aconsejamos realizar más ejemplos con datos reales que te ayuden a profundizar en este conocimiento.
Si quieres seguir formándote en la clasificación estadística, te recomendamos visitar nuestro artículo: «Ejemplo de clasificación estadística usando un dataset de asteroides«.
Desde KeepCoding, sabemos que instruirte por tu cuenta puede resultar complicado y tedioso, por ello, te presentamos el Bootcamp Full Stack Big Data. Gracias a esta formación íntegra e intensivo, podrás contar con todos los conocimientos necesarios para ser un experto en el ecosistema de sistemas, lenguajes y herramientas del Big Data a la par que los llevas a la práctica guiado por grandes profesionales del sector IT. ¡No esperes más para inscribirte y dale un giro a tu carrera profesional!











