¿Sabías que puede utilizarse el k-nn en regresión? En este artículo te mostraremos cómo funcionan los k-nn en regresión por medio de un ejercicio.
Motivación del k-nn en regresión
En regresión, los modelos paramétricos no siempre resultan adecuados para resolver los diferentes problemas de regresión. Por esta razón, se recurre al uso de modelos basados en datos no paramétricos; en este caso es el algoritmo k-nn, que se traduce como k-nearest neighbors o vecinos más cercanos.
Un k-nn en regresión funciona basándonos en datos, mirando las instancias más cercanas y calculando una media. No es paramétrico, de ahí que sea tan efectivo en modelos de regresión.
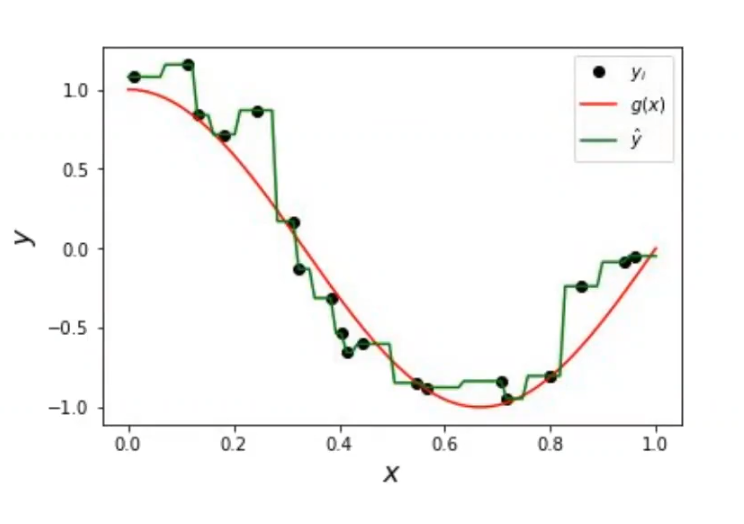
Veamos esta gráfica:
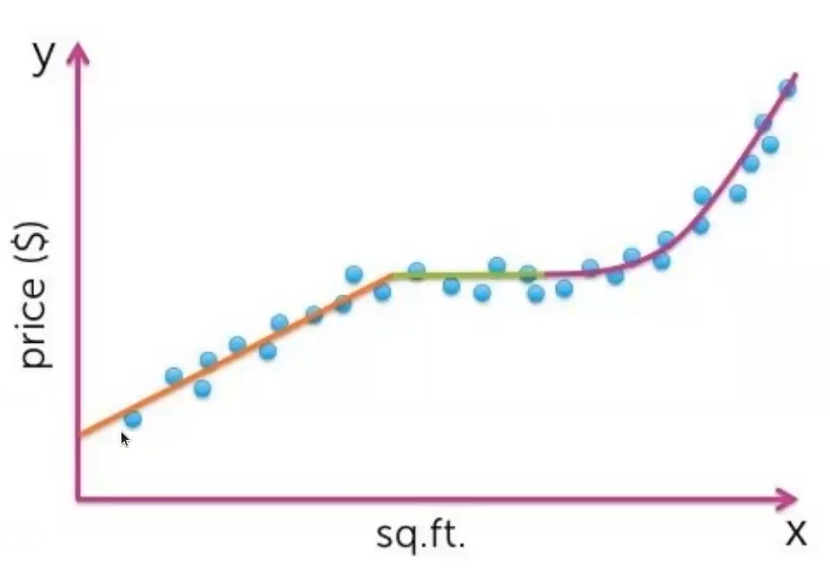
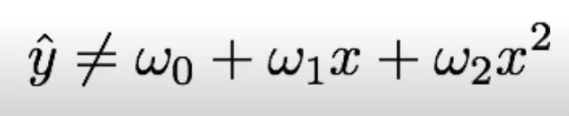
En este caso, no nos vale para nada un modelo lineal, porque tenemos una parte que es no lineal. Tampoco resulta especialmente útil un modelo que sea cuadrático, porque tenemos una parte lineal.
Podríamos ir ajustándolo, metiéndole más y más complejidad para luego regularizarlo, pero también podemos usar un modelo que se base en los datos que tiene. Entonces, el k-nn en regresión mira las instancias más cercanas, va haciendo una media y así con cada sección.
¿Cómo funciona un k-nn en regresión?
El k-nn va a ir mirando y calculando la distancia más cercana y va a hacer una media en función de cuántas instancias escojamos.
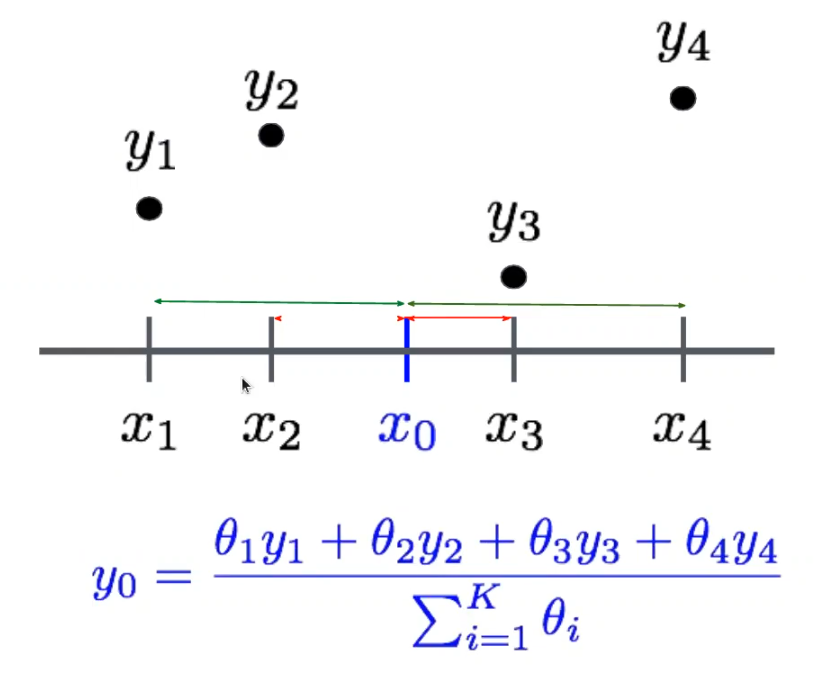
Veamos un ejemplo en el que queremos estimar el precio (y) a partir de sqm (x) en un nuevo punto x0 . ¿Qué es lo que hará un k-nn en regresión? Buscar vecinos de x0
di = llx0 – xill2
El valor estimado es la media de los vecinos:
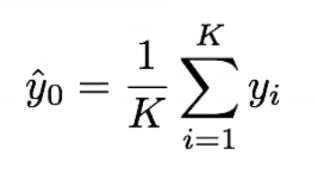
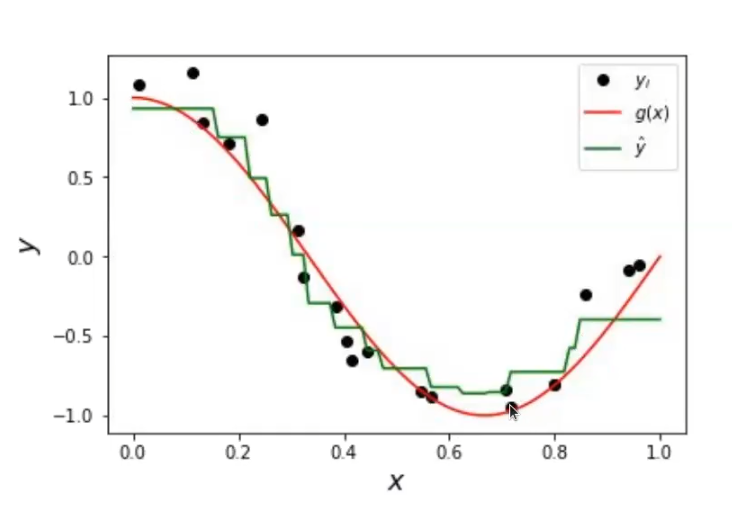
Entonces, si tenemos un K = 1 y miramos solo el vecino más cercano, vamos a tener un buen ajuste si hay mucha densidad de puntos y bajo ruido. Este va a ser un modelo muy complejo y van a estar muy ajustados los datos, pero puede que en ocasiones nos interese.
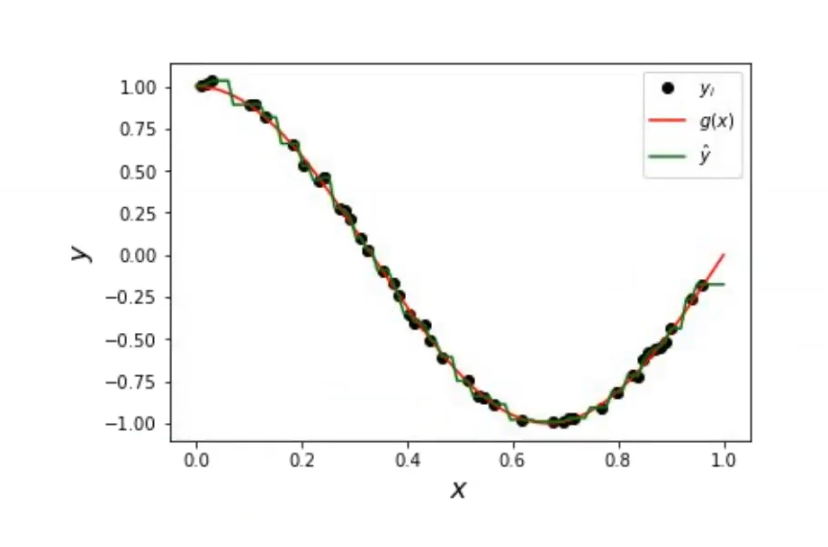
Sin embargo, si no tenemos suficientes datos, el overfitting no va a estar bien ajustado; va a ser, en general, una mala idea. Pero si además de esto tenemos pocos datos, ni siquiera va a ser una cosa usable, ya que vamos a tener regiones sin ejemplos, mal ajustadas y muy sensibles al ruido. Por lo tanto, si no hemos eliminado los outliers correctamente y tenemos de repente un punto mal puesto, ese punto va a impactar mucho en los vecinos.
Ponderación
¿Cuál es la solución a esto? Como ya sabemos, deberíamos aumentar el K, pero esto produciría problemas de desbordamiento. Por ello, la única solución viable sería ponderar la estimación de distancia entre vecinos. Esto implicaría:
- Dar más peso a los más cercanos.
- Reducir el peso de los más alejados.
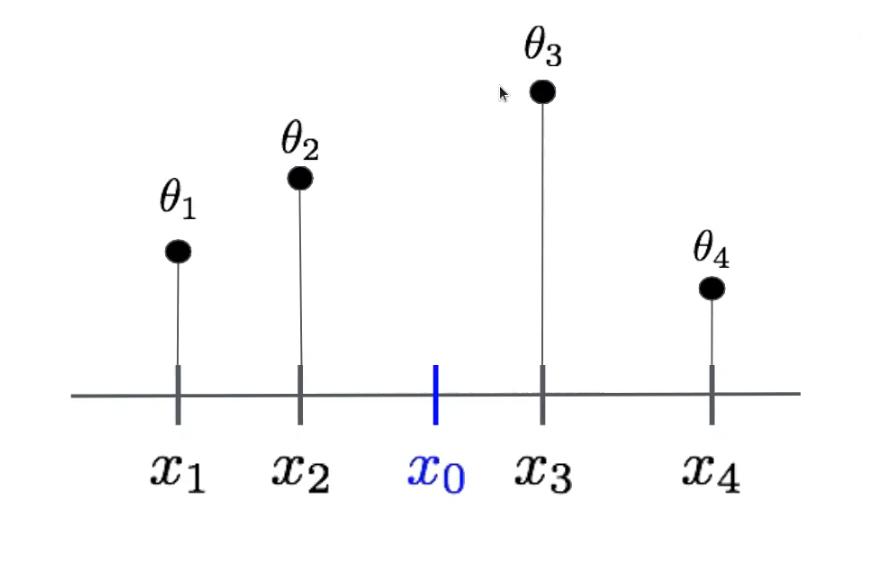
Veamos cómo ponderar la estimación K = 4

¿Cómo elegimos θ?
En función de la distancia:
θi = 1 / di
donde:
di = llx0 – xill2
Si di ↓ ⇒ θi ↑
Si di ↑ ⇒ θi ↓
Podemos utilizar otras opciones, otras medidas de similitud:
θi (σ) =
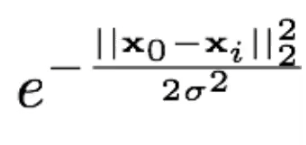
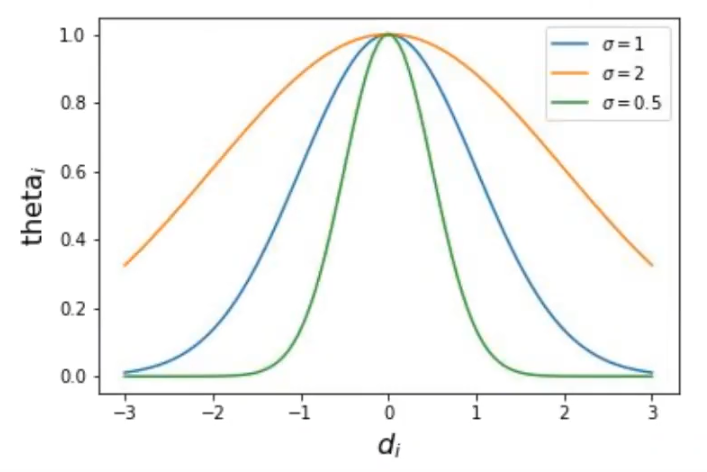
Kernel RBF
RBF: Radial Basis Function
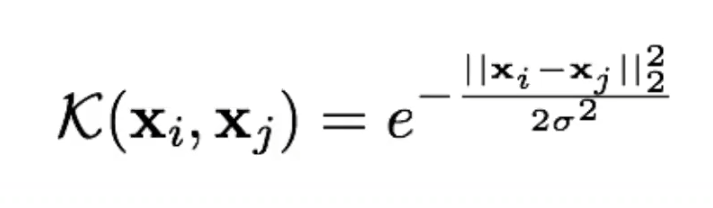
Expresada como:
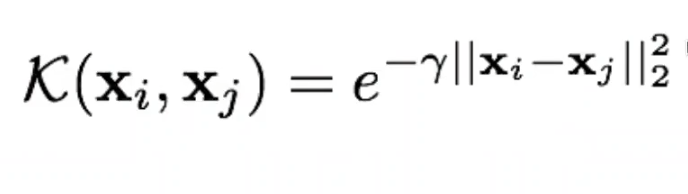
¿Quieres seguir aprendiendo?
Si quieres seguir aprendiendo sobre una de las disciplinas más demandadas y mejor pagadas en la actualidad, no solo en el sector informático, sino también en otras áreas relacionadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta formación intensiva te permitirá adquirir todas las herramientas teóricas y prácticas para seguir escalando hacia la cima del éxito en tu proceso de formación. ¡No dudes más, sigue tu camino y solicita más información ahora!











