La comprobación del teorema central del límite en R se conoce como uno de los cálculos que se utilizan para el conocimiento amplio de los datos estudiados. Forma parte de los estadísticos que se utilizan para hacer un reconocimiento de la información, es decir, conocer cómo se comportan y qué tipo de preguntas se les puede realizar.
Por esta razón, en este post, te explicamos qué es la comprobación del teorema central del límite en R, el lenguaje de programación predilecto para los estudios estadísticos del Big Data.
¿Qué es R en estadística Big Data?
Como se ya hemos mencionado, R es el lenguaje de programación más utilizado para los análisis estadísticos en el manejo de los macrodatos. La principal razón es que este lenguaje se diseñó orientado a la estadística, a diferencia, por ejemplo, de Python, que es un lenguaje de programación más generalista, a pesar de que también se emplea con regularidad.
Por otra parte, R es un lenguaje de programación de tipo open source (código abierto), gracias a lo que podrás descargar su código y contribuir a la ciencia del manejo de los datos. Ahora que ya sabes a qué hace referencia R, podrás comprender mejor qué es la comprobación del teorema central del límite en R o central R.
¿Qué es el teorema central límite en R?
La comprobación del teorema central del límite en estadística es una forma de calcular la suma de variables para garantizar que, cuando estas variables son demasiadas, la distribución siga siendo una distribución normal.
Por otra parte, para que se produzca la comprobación del teorema central del límite en R se establece que, para distribuciones independientes e idénticamente distribuidas con la media, se calcule así:
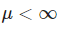
Además, se establece que la varianza se averigüe con la siguiente fórmula:
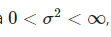
De esta manera, la suma de un gran número de variables aleatorias se distribuye aproximadamente como una normal.
Comprobación del teorema central del límite en R
Para comprender más en profundidad la comprobación del teorema central del límite en R te presentamos el siguiente ejemplo: vas a crear vectores de 10.000 entradas que sigan una distribución uniforme entre -1 y 1.
Posteriormente, vas a sumar los vectores entre sí y a representar la función de la densidad. Debes tener en cuenta que, cuantos más vectores de distribución uniforme sumes, más tenderá la curva a una gaussiana.
Su desarrollo se presentaría de la siguiente manera:
data.frame(val=as.numeric(),numFunctions=as.numeric())
numSamples<-1000
myRandomDataFrame<-data.frame(val=as.numeric(),numFunctions=as.numeric())
for (numFunctions in c(1,10,100)){
myRandomVector<-rep(0,numSamples)
for (i in 1:numFunctions){
myRandomVector<-myRandomVector+runif(numSamples,min = -1,max = 1)
}
myRandomVector<-myRandomVector
myRandomDataFrame<-rbind(myRandomDataFrame,data.frame(val=myRandomVector,numFunctions=numFunctions))
}
myRandomDataFrame$numFunctions<-as.factor(myRandomDataFrame$numFunctions)
sd10<-sd(myRandomDataFrame$val[myRandomDataFrame$numFunctions==10])
paste("Desviación típica sumando 10 uniformes:",sd10)
paste("Desviación típica sumando 100 uniformes:",sd(myRandomDataFrame$val[myRandomDataFrame$numFunctions==100]))
require(ggplot2)
ggplot(data=myRandomDataFrame, aes(x=val,color=numFunctions)) +
#geom_density(kernel="rectangular",bw=0.07)
stat_function(fun=dnorm,args = list(mean = 0, sd=sd10),
geom="area",color="#a98600",fill="yellow",alpha=0.3)+
geom_density(kernel="rectangular")
¿Quieres saber más del Big Data?
Por medio de este post, te has podido familiarizar con lo que es la comprobación del teorema central del límite en R; no obstante, este lenguaje de programación ofrece muchas más fórmulas para llevar a cabo cálculos estadísticos en el manejo del Big Data. ¡Conocer estos comandos es fundamental si quieres saber más sobre los macrodatos!
Por esta razón, desde KeepCoding te aconsejamos echarle un vistazo al Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning si lo que deseas es continuar aprendiendo y formarte como un data scientist profesional. A través de 11 módulos y de la mano de grandes expertos en el mundo del Big Data, podrás instruirte en los sistemas, lenguajes y programas más importantes para el manejo de los macrodatos. ¡No esperes más para inscribirte!



