El cross validation en R o validación cruzada es un método que se utiliza para estimar las métricas de rendimiento y precisión en el entrenamiento de un modelo de machine learning o aprendizaje automático. Se usa mucho en la protección de modelos predictivos, para prevenir overfittings en casos donde la cantidad de datos puede ser limitada.
¿Quieres saber cómo utilizar el cross validation en R? En este artículo te enseñamos cómo hacerlo.
¿Cómo funciona el cross validation en R?
Lo que hace el cross validation en R es que el conjunto de datos que nosotros le pasamos los divide internamente entre train y test. Lo divide, por ejemplo, en 5 grupos y de esos 5 grupos utiliza 4 para training y uno para test. Pero no siempre utiliza esos grupos, luego los vuelve a cambiar, por lo que si al final tienes un k-fold de 5, lo que tienes son 5 medidas de error.
El procedimiento del cross validation en R tiene un solo parámetro de ajuste denominado k, que se refiere a la cantidad de grupos en los que se dividirá una muestra de datos determinada. Cuando se elige un valor específico para k, puede usarse en lugar de k en la referencia al modelo, como k = 18 se convierte en una validación cruzada de 18 veces.
Procedimiento a seguir para el cross validation en R
Lo primero que hacemos para las técnicas de cross validation en R es la evaluación del modelo. Para ello, dividimos los datos originales en k-folds. Estos se dividen en conjunto de entrenamiento del modelo y en datos de prueba.
Luego entrenamos con (k-1) folds.
Posteriormente, calculamos el error con 1 fold.
Las medidas de error obtenidas nos permiten calcular una media del error y una desviación típica, un margen de error, que es lo que haremos a continuación:
In (21) : cvfit <- cv.glmnet (as.matrix (df [ , c ('x1', 'x2', 'x3')]), as.matrix (df [ , 'y']), nfolds = 10, alpha = 1, standarize = F)
plot (cvfit)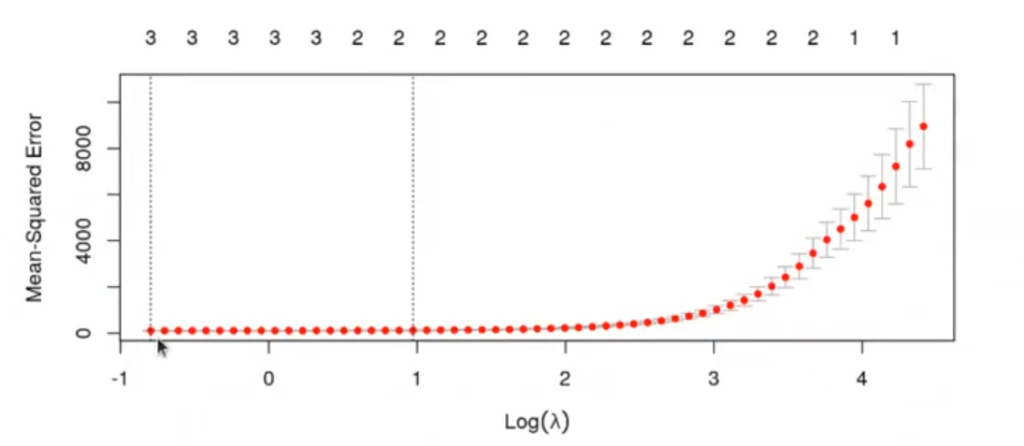
El modelo que tiene un error cuadrático medio más bajo aparece en la variable cvfitSlambda.min.
El modelo que tiene un mayor valor de λ, cuya varianza del error está dentro de 1 desviación típica del mínimo, aparece en la variable cvfitSlambda.lse.
Al hacer cross validation, el MSE no será un valor único, sino que tendremos nfolds diferentes. De todos estos MSE podemos calcular la media y la desviación típica. El valor de lambda 1 se refiere al modelo más sencillo (λ más alto), que no se diferencia considerablemente del mínimo.
In [ ] : options (repr.plot.height = 2, repr.plot.width = 5)
lamda se <-1
qsd009 <- function (x) {
out <- dnorm(x)
out [x> lamda_se | x< - lamda_se <- NA
out
}
xdf <- data.frame (z = c (-4, 4))
ggplot (xdf, aes (x = z)) + stat_function (fun = dnorm) +
stat_function (fun = qsd009, geom = "area", fill = "red") +
geom_text (x = 0, y = 0.2, size = 4, label = paste0 (100 * round (pnorm (lamda_se) - pnorm ( - lamda_se), 4) , "%")) +
theme linedraw()
options (repr.plot.height = 7, repr.plot.width = 7)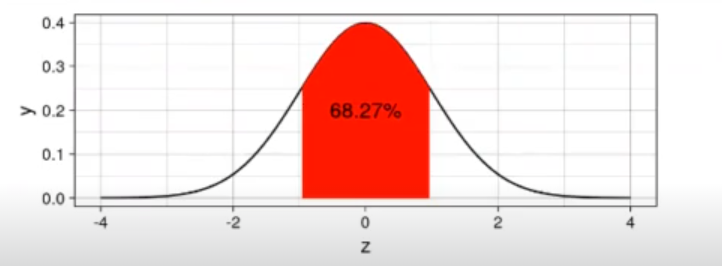
In [ ] : cvfit$lambda.min
cvfit$lambda.Ise0.451184203345069
2.64259526742003
In [24] : coef (cvfit, s = "lambda.lse")4 x 1 sparse Matrix of class «dgCMatrix»
s1
(Intercept) : 2.324143
x1 : .
x2 : -4.710797
x3 : 3.896718
Su R ^ 2 estimado será:
In [25] : cvfit$glmnet.fit$dev.ratio [which (cvfit$glmnet.fit$lambda == cvfit$lambda.lse)]0.8732001745813
En resumen, para hacer una predicción Lasso con glmnet tendríamos lo siguiente:
In [26] : cvfit <- cv.glmnet (as.matrix (df [ , c ('x1', 'x2', 'x3')]), as.matrix (df [ , 'y']), nfolds = 10, alpha = 1, standarize = F)
df_tests <- get_example_data_frame (n = 100)
df_test [ , c ("pred")] <- predict (cvfit, newx = as.matrix (df_test [ , c ('x1', 'x2', 'x3')]), s = cvfit$lambda.Ise)
head(df_test)
caret::postResample (df_test$y.df_test$pred)| x1 | x2 | x3 | y | pred | |
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl [ , 1]> | |
| 1 | 1.9361383 | 3.972058 | 5.3340171 | 11.30191 | 1.534398 |
| 2 | 4.8417332 | 16.173018 | 8.0295401 | -38.64590 | -42.743196 |
| 3 | 9.0567426 | -9.289640 | 9.5627518 | 79.14404 | 83.899767 |
| 4 | -0.2075752 | 15.810312 | -0.2039507 | -62.10379 | -73.203000 |
| 5 | -8.3342531 | 3.095098 | -45.7535663 | -188.56495 | -190.972616 |
| 6 | -4.8014400 | 22.613531 | -20.9445618 | -192.01536 | -186.498193 |
RMSE: 11.0277352597337
Rsquared: 0.988121820579942
MAE: 9.14338178003851
¿Qué sigue?
Ahora que hemos visto cómo funciona el cross validation en R y la librería glmnet, junto a la regularización Lasso, podemos pasar a otros conceptos más complejos que podrás abordar en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En unos pocos meses, podrás aprender todo lo necesario para incursionar en un mercado laboral muy prolífico que te brindará mejores posibilidades de empleo en el sector IT. ¡No esperes para solicitar más información y sigue forjando tu futuro!











