En este ejemplo de regresión logística veremos lo que podría ocurrir cuando tenemos dos variables correlacionadas estrechamente.
Recordemos que la regresión logística es un proceso de modelado para calcular la probabilidad de un resultado discreto dada una variable de entrada. Esta se utiliza mucho cuando la variable dependiente es también una variable categórica.
Ejercicio de regresión logística: dos variables correlacionadas
En este ejemplo vemos cómo hay dos variables correlacionadas y trabajaremos con un ejemplo para determinar si un número de datos dados es ruido o es avión y qué cantidad es cada cosa.
#dos variables correlacionadas
radar <- read.csv ("data/radar.csv", stringsAsFactors = T) l> select (-X)
radar$tipo <- relevel (radar$tipo, ref = "ruido")
str (radar)
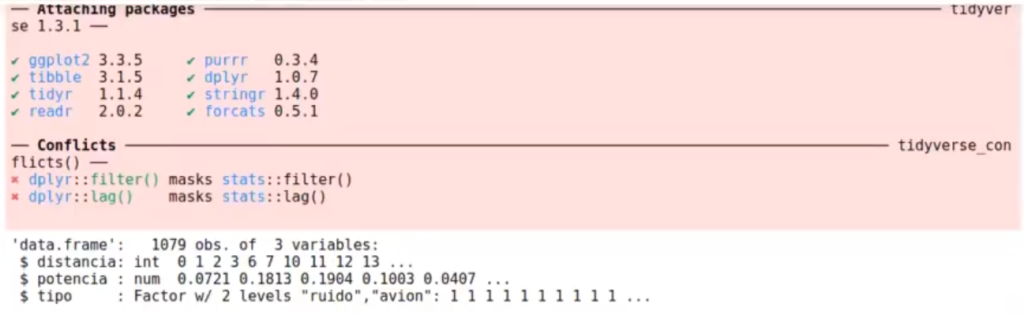
‘data.frame’: 1079 obs. of 3 variables:
$ distancia: int 0 1 2 3 6 7 10 11 12 13 …
$ potencia: num 0.0721 0.1813 0.1904 0.1003 0.0407 …
$ tipo: Factor w / 2 levels «ruido», «avion»: 1 1 1 1 1 1 1 1 1 1 …
#dos variables correlacionadas set.seed (123) itrain <- sample (1 : nrow (radar), round (nrow (radar) * 0.7)) radar.train <- radar [itrain, ] radar.test <- radar [-itrain, ] summary (radar.train) summary (radar.test)
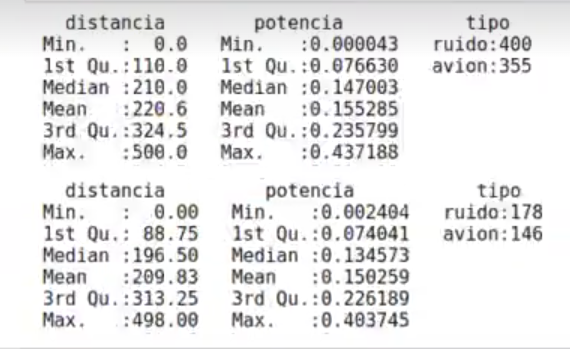
Lo siguiente nos calcula la distancia y la potencia y cómo funcionan estas:
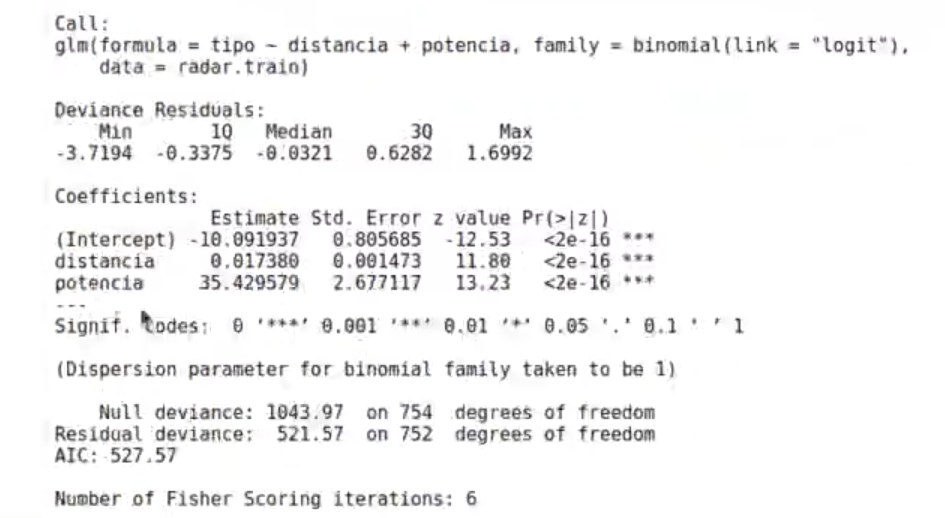
#dos variables correlacionadas model_radar <- glm (data = radar.train, formula = tipo~ distancia + potencia, family = binomial (link = 'logit")) summary (model_radar)
#dos variables correlacionadas
mcl <- table (real = radar.teststipo, pred = factor (predict (model_radar, radar.test) > 0, labels = c ('ruido', 'avion')))
mcl
| real | ruido | avión |
| ruido | 165 | 13 |
| avión | 11 | 135 |
Con correlaciones muy altas
Vamos a ver un ejemplo en el que hemos creado unas nuevas variables. Por ejemplo, además de la potencia y la distancia normales, también tenemos la potencia en nanovatios (potenciaW) y la distancia en metros (distanciaM).
Entonces, estas nuevas variables, si te fijas bien, tienen una correlación de 0.99. Esto es porque estamos haciendo un round y la correlación no llega a ser 1. En cambio, con la distancia pasa algo distinto, ya que aquí el valor sí es uno; esto se da porque no estamos haciendo ningún round y lo estamos multiplicando por 1000.
#dos variables correlacionadas radar$potencianW <- round (radar$potencia * 1000) radar$distanciaM <- radar$distancia * 1000 cor (radar |> select (-tipo))
| distancia | potencia | potencianW | distanciaM | |
| distancia | 1.0000000 | -0.3604463 | -0.3604456 | 1.0000000 |
| potencia | -0.3604463 | 1.0000000 | 0.9999951 | -0.3604463 |
| potenciaW | -0.3604456 | 0.9999951 | 1.0000000 | -0.3604456 |
| distanciaM | 1.0000000 | -0.3604463 | -0.3604456 | 1.0000000 |
¿Cómo se interpreta un modelo de estos, con coeficientes tan altos?
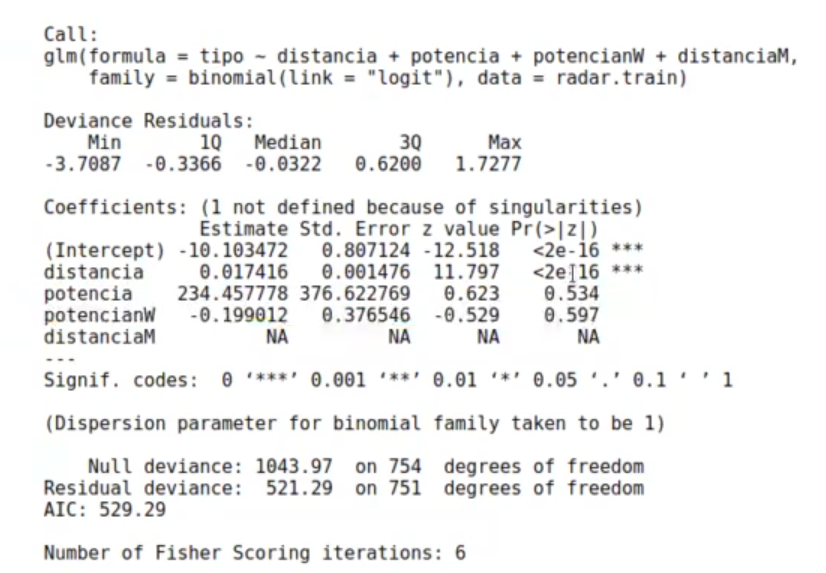
Si nos fijamos en el siguiente resultado, al que tiene correlación 1 le ha puesto NA. Es como meter la misma variable, ya que si insertas la misma variable dos veces, una de las dos será NA, porque piensa que ese coeficiente no vale o no es útil.
Hay ocasiones en las que, si el coeficiente es exactamente el mismo, es decir, si los dos están cambiando exactamente igual y si la correlación es precisamente de 1, uno de ellos lo va a poner como NA.
En distancia y potenciaW, cuyos coeficientes no son iguales del todo, por lo que no tienen tanta correlación, nos ha bajado muchísimo el pvalor.
#dos variables correlacionadas set.seed (123) itrain <- sample (1 : nrow (radar), round (nrow (radar) * 0.7)) radar.train <- radar [itrain, ] radar.test <- radar [-itrain, ] summary (radar.train) summary (radar.test)
#dos variables correlacionadas
mc2 <- table (real = radar.teststipo, pred = factor (predict (model_radar, radar.test) > 0, labels = c ('ruido', 'avion')))
mc2
Warning message in predict.lm (object, newdata, se.fit, scale = 1, type = if (type == : «prediction from a rank – deficient fit may be misleading»
| real | ruido | avión |
| ruido | 165 | 13 |
| avión | 11 | 135 |
Las predicciones, pese a todos los inconvenientes de todos los coeficientes, no se han visto perjudicadas.
Por eso es bueno aclara que, aunque las correlaciones sean malas y el sistema nos diga que es mejor eliminarlas, tenemos que mirar qué es lo que más nos favorece en relación a nuestro objetivo.
Ahora que has visto de qué tratan las variables correlacionadas, es el momento de ir un paso más allá y seguir con tu formación para convertirte en un experto. Para ello, te invitamos a formar parte de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos necesarios para incursionar en un mundo tan complejo como interesante. ¡Anímate a perseguir tus sueños y solicita ahora más información!











