Decay al learning rate en Deep Learning es uno de los métodos más importantes para el manejo de redes de neuronas profundas, por ello, en este recorrido se conoce su implementación como uno de unos los más complejos y necesarios.

Por este motivo, en este post, te explicamos qué es el decay al learning rate en Deep Learning.

¿Qué encontrarás en este post?

Decay al learning rate en Deep Learning

En primer lugar, aplicar el decay al learning rate en Deep Learning es una opción muy utilizada para lograr un learning rate óptimo, conforme va disminuyendo la función de pérdidas (lo que indica que estamos llegando al mínimo buscado).

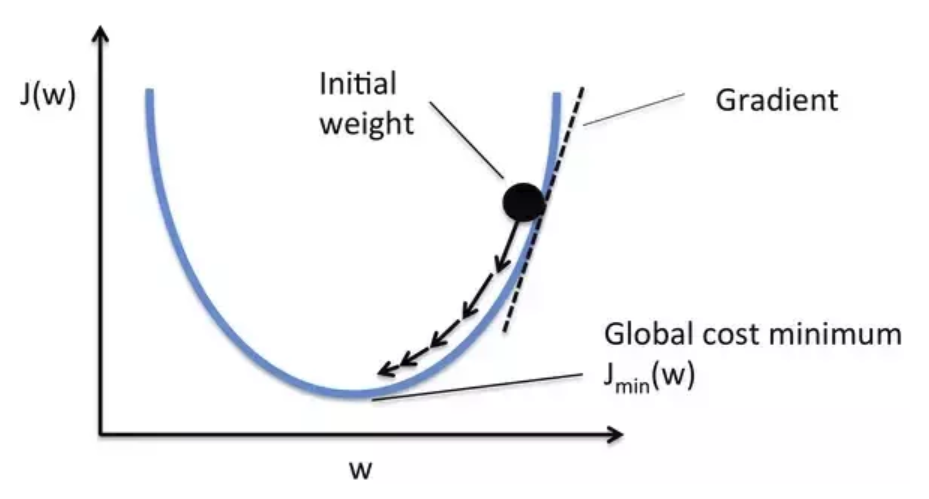
Como puedes imaginar, el learning rate es un parámetro muy importante. De manera que, si ponemos un learning rate muy alto, podemos saltarnos el mínimo. En cambio, si ponemos un learning rate muy bajo, igual tendríamos que esperar una eternidad antes de ver el resultado. ¿Cómo podemos arreglar esto?

Una forma de solucionarlo sería dar pasos más grandes al principio y, conforme nos aproximamos a la meta, empezar a disminuir su longitud para no pasárnosla. A esto se le llama decay al learning rate en Deep Learning y, a continuación, te lo ilustramos con un ejemplo.

Por ejemplo

# definimos la función para entrenar nuestra red con los parámetros deseados
def train_network_decay(learning_rate, lr_decay, batch_size, n_epochs):
  
  # creamos los contenedores para nuestras entradas y salidas
  x = tf.placeholder(tf.float32, [None, 784]) # imágenes del mnist: 28*28=784
  y = tf.placeholder(tf.float32, [None, 10]) # número indicando la clase 0-9 => 10 clases
  
  # creamos las variables W y b para el entrenamiento
  W = tf.Variable(tf.zeros([784, 10]))
  b = tf.Variable(tf.zeros([10]))

  # por último, construimos el modelo
  pred = tf.nn.softmax(tf.matmul(x, W) + b)

  # ahora, definimos nuestra función de pérdidas: la cros-entropía
  # a veces la llaman loss, a veces cost; es lo mismo
  cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))

  # calculamos los gradientes (gradient descent)
  grad_W, grad_b = tf.gradients(xs=[W, b], ys=cost)
  
  # definimos las operaciones para actualizar los pesos con los gradientes calculados
  # e implementamos el learning rate decay **IMPORTANTE**
  new_W = W.assign(W - learning_rate * (1-lr_decay) * grad_W)
  new_b = b.assign(b - learning_rate * (1-lr_decay) * grad_b)

  # inicializamos las variables
  init = tf.global_variables_initializer()
  
  # para almacenar el histórico de costes
  costs = []
  # inicializamos current_lr
  current_lr = learning_rate
  # empezamos la sesión
  with tf.Session() as sess:
      sess.run(init)

      # entrenamiento de nuestra red
      for epoch in range(n_epochs):
          avg_cost = 0.
          total_batch = int(mnist.train.num_examples/batch_size)

          # En vez de actualizar los pesos para cada imagen, podríamos
          # hacerlo de X en X imágenes
          for i in range(total_batch):
              batch_xs, batch_ys = mnist.train.next_batch(batch_size)

              # ejecutamos la optimización
              Wc, bc, c = sess.run([new_W, new_b ,cost], feed_dict={x: batch_xs,
                                                                    y: batch_ys})

              # calculamos el coste teniendo en cuenta los batches que hay
              avg_cost += c / total_batch
              
          # actualizamos el learning_rate igual que lo hace tensorflow
          current_lr = current_lr * (1-lr_decay)

          # guardamos nuestro coste en el histórico
          costs.append(avg_cost)
          
          # Imprimimos las iteraciones
          # current_lr = learning_rate * (1-lr_decay) ** (epoch * batch_size + i)
          print("[{}] cost: {} lr: {}".format(epoch, avg_cost, current_lr))

      print("Entrenamiento finalizado")
# comprobamos lo que ha aprendido nuestra red
      correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))

      # ahora, calculamos el accuracy (precisión)
      accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
      print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
      
  # veamos nuestra función de pérdidas con respecto a las épocas ejecutadas
  plt.plot(np.arange(0, n_epochs), costs)
  plt.title("Training Loss")
  plt.xlabel("Epoch #")
plt.ylabel("Loss")

# vamos a probar nuestra red con decay al learning rate en Deep Learning
learning_rate = 0.2
lr_decay = 1e-4
n_epochs = 10
batch_size = 128
train_network_decay(learning_rate, lr_decay, batch_size, n_epochs)

Decay al learning rate en Deep Learning 2

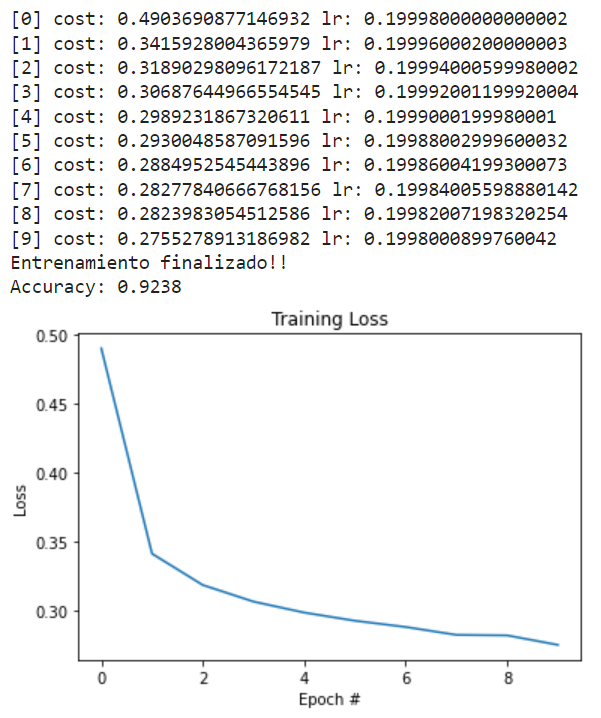
Con esta simple mejora, hemos sido capaces de mejorar la precisión con respecto al learning rate óptimo, que habíamos definido como 0.1. También existen métodos más complejos de aplicar el decay que producen mejores resultados.

Cabe destacar que esta implementación de decay al learning rate en Deep Learning es muy básica. En realidad, existen distintos tipos de “calendarios” de actualización de learning rate: de escalón, polinomial, etc. Al final, lo que hacen todos es modificar el learning rate de acuerdo a una ecuación o regla.

En este post, te hemos explicado qué es el decay al learning rate en Deep Learning, de manera que ahora puedas emplearlo en tu procesamiento de los macrodatos. No obstante, sabemos que querrás ampliar tu conocimiento en esta área del manejo Big Data y en KeepCoding, ¡tenemos la opción perfecta para ti!

Para facilitarte el proceso de aprendizaje, te brindamos el Bootcamp de Big Data y Data Science, por medio del que te formarás en el proceso de ingesta, clasificación, resguardo, procesamiento y presentación de los macrodatos gracias al uso de diferentes herramientas, sistemas y lenguajes. Al finalizar, en menos de nueve meses, serás capaz de reconocer las ventajas e inconvenientes de los distintos programas estudiados. ¡Échale un vistazo a nuestro temario e inscríbete ya!