¿Sabes qué es la dependencia lineal de vectores con sympy y cómo funciona? ¿Qué sucedería si cogiéramos la siguiente ecuación, que lo que hacía era multiplicar escalares por vectores, y la igualáramos a cero e intentáramos despejar los escalares? En este artículo te lo enseñamos.
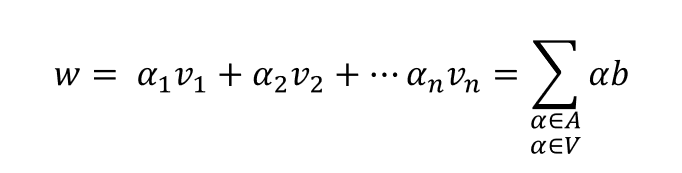
¿Qué es la dependencia lineal de vectores con sympy?
Dado un conjunto finito de vectores x1, x2, …, xn, se dice que los mismos son linealmente independientes solo si los únicos escalares α1, α2, …, αn, que satisfacen la ecuación son todos ceros.
0 = α1 x1 + … + αn xn
α1 = α2 = … = αn = 0
En caso de que no se cumpla, es decir, existe una solución a la ecuación anterior en la que no todos los escalares son ceros, a esta solución se llama no trivial y se dice que los vectores son linealmente dependientes.
#dependencia lineal de vectores con sympy
#2x + 3y //// a * vector_1 + b * vector_2 = 0Ejercicio sobre dependencia lineal de vectores con sympy
Supongamos que queremos determinar si los siguientes vectores son linealmente independientes:
x1 = [1.2, 1.1]
x2 = [-2.2, 1.4]
Para calcular si son linealmente independientes, debemos resolver el siguiente sistema de ecuaciones y verificar si la única solución es aquella en la que los escalares sean ceros.
α1 [1.2, 1.1] + α2 [-2.2, 1.4] = 0
En la ecuación, α1 y α2 son escalares, mientras que [1.2, 1.1] y [-2.2, 1.4] son vectores.
Vamos a ver una de las formas de resolver este ejercicio sobre dependencia lineal, que es usando la librería sympy:
#dependencia lineal de vectores con sympy
import sympy as sp
import numpy as np
x = sp.Symbol ('alpha1')
y = sp.Symbol ('alpha2')
#Primeros componentes, segundos componentes
resultado = sp.solve ([1.2 * x - 2.2 * y, 1.1 * x + 1.4 * y], [x, y])
resultado{α1 : 0.0, α2: 0.0}
Aquí lo que nos dice es que los únicos valores que pueden tomar los dos escalares para que la ecuación sea completa y satisfecha es cero. Al ser cero, el resultado nos indica que son linealmente independientes. En caso contrario, serían linealmente dependientes.
¿Cómo continuar?
Ahora que hemos visto cómo funciona la estructura de un espacio vectorial, puedes seguir aprendiendo sobre el sector IT en el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación intensiva e íntegra podrás adquirir todos los conocimientos teóricos y prácticos que requieres para entrar en el mercado laboral en menos de un año. ¡Anímate a impulsar tu vida profesional y solicita más información ya mismo!



