El descenso de gradiente en una red neuronal de TensorFlow forma parte de los conocimientos necesarios para enfrentarte al campo del Deep Learning dentro del manejo de los macrodatos. Por este motivo, en este post, te presentamos cómo funciona el descenso de gradiente en una red neuronal de TensorFlow.

En este post encontrarás: ocultar

1 Descenso de gradiente en una red neuronal de TensorFlow

1.1 ¿Cómo lo haríamos con TF 2.0?

2 ¿Cuál es el siguiente paso para aprender sobre Big Data?

Descenso de gradiente en una red neuronal de TensorFlow

Para explicar cómo funciona el descenso de gradiente en una red neuronal de TensorFlow, vamos a presentar una serie de ejemplos para que lo comprendas en profundidad.

Para ello, en este ejemplo de descenso de gradiente en una red neuronal de TensorFlow hay que considerar el dataset MNIST de imágenes monocromas de 28×28 píxeles de dígitos del 0 al 9:

Vamos a implementar una red capaz de clasificarlos, ¡a ver a qué precisión somos capaces de llegar!

# Seleccionamos la version 1.x de TF
%tensorflow_version 1.x

TensorFlow 1.x selected.

# imports necesarios
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# importamos el dataset MNIST y cargamos los datos
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

# parámetros
learning_rate = 0.01
n_epochs = 100
batch_size = 100

# Creamos los contenedores para nuestras entradas y salidas
x = tf.placeholder(tf.float32, [None, 784]) # imágenes del mnist: 28*28=784
y = tf.placeholder(tf.float32, [None, 10]) # número indicando la clase 0-9 => 10 clases

# y creamos las variables W y b para el entrenamiento
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

# por último, construimos el modelo
pred = tf.nn.softmax(tf.matmul(x, W) + b)

# ahora, en este descenso de gradiente en una red neuronal de TensorFlow definimos nuestra función de pérdidas: esta vez, la cros-entropía
# a veces la llaman loss, a veces cost => es lo mismo
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), axis=1))

# calculamos los gradientes (gradient descent)
grad_W, grad_b = tf.gradients(xs=[W, b], ys=cost)

# definimos las operaciones para actualizar los pesos con los gradientes calculados
# y el learning rate
new_W = W.assign(W - learning_rate * grad_W)
new_b = b.assign(b - learning_rate * grad_b)

# inicializamos las variables
init = tf.global_variables_initializer()

# para almacenar el histórico de costes
costs = []
# empezamos la sesión
with tf.Session() as sess:
    sess.run(init)

    # entrenamiento de nuestra red
    for epoch in range(n_epochs):
        avg_cost = 0.
        total_batch = int(mnist.train.num_examples/batch_size)
        
        # y si en vez de actualizar los pesos para cada imagen, ¿lo hacemos
        # de X en X imágenes?
        for i in range(total_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            
            # ejecutamos la optimización
            _, _, c = sess.run([new_W, new_b ,cost], feed_dict={x: batch_xs,
                                                       y: batch_ys})
            
            # calculamos el coste teniendo en cuenta los batches que hay
            avg_cost += c / total_batch
            
        # guardamos nuestro coste en el histórico
        costs.append(avg_cost)
        
        # imprimimos las iteraciones
        print("[{}] cost: {}".format(epoch, avg_cost))

    print("Entrenamiento finalizado!!")

    # comprobamos lo que ha aprendido nuestra red
    correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
    
    # calculamos el accuracy (precisión)
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

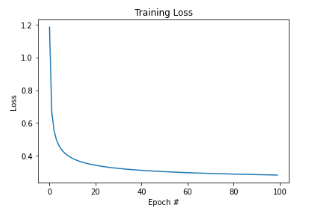
# veamos nuestra función de pérdidas con respecto a las épocas ejecutadas
plt.plot(np.arange(0, n_epochs), costs)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")

Text(0, 0.5, ‘Loss’)

¿Cómo lo haríamos con TF 2.0?

# Seleccionamos la version 2.x de TF
%tensorflow_version 2.x

# imports necesarios
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

# parámetros
learning_rate = 0.01
n_epochs = 100
batch_size = 100

# cargamos el dataset
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

Comprobamos cómo es el dataset que hemos cargado y si necesita normalización:

x_train.shape

(60000, 28, 28)

x_test.shape

(10000, 28, 28)

x_train.max()

255

x_test.max()

255

# vamos a normalizar entre 0 y 1
x_train = x_train / 255.
x_test = x_test / 255.

print(x_train.max())
print(x_test.max())

1.0
1.0
También necesitamos convertir las imágenes a vectores, porque aún no hemos visto cómo podemos implementar un modelo que trabaje con imágenes. Vamos a ver cómo lo hacemos:

x_train = tf.reshape(x_train, shape=(60000, -1))
print(x_train)

x_test = tf.reshape(x_test, shape=(10000, -1))
print(x_test)

Ahora nuestros datos ya están en formato [N_instancias, variables] (60000 instancias, 784 (28+28) píxeles).

A continuación, debemos fijarnos en el formato de nuestras etiquetas, que en este caso tendrán que estar codificadas en one-hot. De lo contrario, obtendremos un error como este:

Vamos a ver cómo hacerlo:

print(y_train.shape)
print(y_test.shape)

(60000,)
(10000,)

# convertimos las etiquetas a one-hot
y_train = tf.one_hot(y_train, depth=10)
y_test = tf.one_hot(y_test, depth=10)

print(y_train.shape)
print(y_test.shape)

(60000, 10)
(10000, 10)
Ya las tenemos codificadas como one-hot.

Por último, debemos fijarnos en los tipos de datos con los que estamos trabajando. TF exige que los tipos coincidan.

print(x_train.dtype)
print(x_test.dtype)
print(y_train.dtype)
print(y_test.dtype)

# convertimos las etiquetas a float64
y_train = tf.cast(y_train, 'float64')
y_test = tf.cast(y_test, 'float64')

print(x_train.dtype)
print(x_test.dtype)
print(y_train.dtype)
print(y_test.dtype)

¡Perfecto! Ahora sí que estamos preparados. Si no hubiéramos hecho esta conversión, habríamos obtenido un error como este:

Nos creamos ahora el iterador para que recorra nuestro dataset. Aquí podéis leer más sobre tf.data.

train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_ds = train_ds.shuffle(10000).batch(batch_size)

# para el conjunto de test no vamos a necesitar el dataloader porque
# no vamos a procesar los datos por batches, sino todos a la vez, así 
# que utilizaremos x_test y y_test. 
# Si fuesemos a procesarlo por batches, se haría así:
# test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
# test_ds = test_ds.batch(batch_size)

# ¿Cuántas iteraciones habrá por época? 
# en una época se tienen que ver todos los elementos del dataset, y estamos
# pasándole los elementos de 100 en 100, así que habrá 60000 / 100 = 600 épocas
total_batch = x_train.shape[0] // batch_size
print(total_batch)

600

# creamos las variables W y b para el entrenamiento
W = tf.zeros([784, 10], tf.double)
b = tf.zeros([10], tf.double)

# para almacenar el histórico de costes
costs = []
# entrenamiento de nuestra red
for epoch in range(n_epochs):
    avg_cost = 0.
    
    # ¿si en vez de actualizar los pesos para cada imagen, lo hacemos
    # de X en X imágenes?
    for batch_xs, batch_ys in train_ds:
        # empezamos con la optimización
  
        # usamos tf.GradientTape, que lleva un control de las variables
        # para poder calcular sus gradientes
        with tf.GradientTape() as tape:
            # le indicamos que "vigile" las variables a optimizar
            tape.watch(W)
            tape.watch(b)
            
            # ejecutamos el modelo
            pred = tf.nn.softmax(tf.matmul(batch_xs, W) + b)

            # ahora, definimos nuestra función de pérdidas: esta vez, la cros-entropía
            # a veces la llaman loss, a veces cost => es lo mismo
            cost = tf.reduce_mean(-tf.reduce_sum(batch_ys*tf.math.log(pred), axis=1))

            # calculamos los gradientes (gradient descent)
            grad_W, grad_b = tape.gradient(cost, [W, b])

            # definimos las operaciones para actualizar los pesos con los gradientes calculados
            # y el learning rate
            W = W - learning_rate * grad_W
            b = b - learning_rate * grad_b

        # calculamos el coste teniendo en cuenta los batches que hay
        avg_cost += cost / total_batch
        
    # guardamos nuestro coste en el histórico
    costs.append(avg_cost)
    
    # imprimimos las iteraciones
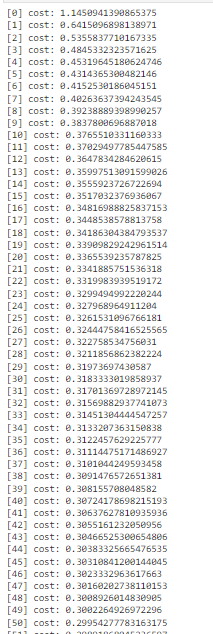
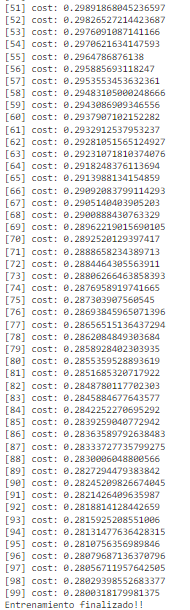
    print("[{}] cost: {}".format(epoch, avg_cost))
print("Entrenamiento finalizado!!")

# comprobamos lo que ha aprendido nuestra red
pred = tf.nn.softmax(tf.matmul(x_test, W) + b)
correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y_test, 1))

# calculamos el accuracy (precisión)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print("Accuracy:", accuracy.numpy())

Accuracy: 0.9225

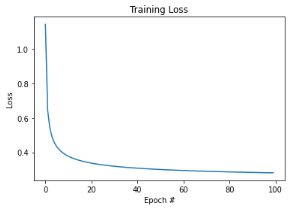
# veamos nuestra función de pérdidas con respecto a las épocas ejecutadas
plt.plot(np.arange(0, n_epochs), costs)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")

Text(0, 0.5, ‘Loss’)

¡Ahí lo tienes! Hemos llegado al mismo sitio de una forma más sencilla e intuitiva.

Seguramente te estés preguntando por qué va más lento que con TF1.x. Esto se debe a varias causas, pero la principal es que en TF 1.x al definir el grafo se realizan determinadas optimizaciones que permiten una ejecución más rápida.

¿Cuál es el siguiente paso para aprender sobre Big Data?

En el desarrollo de este post, te hemos expuesto qué es el descenso de gradiente en una red neuronal de TensorFlow, sin embargo, este es un proceso que debes llevar a la práctica. Para continuar con tu formación, te recomendamos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. ¡Inscríbete ahora y conviértete en un experto en pocos meses!