Con el desarrollo masivo de datos que se produce cada segundo en la actualidad, cálculos como la desigualdad de Chebyshev en estadística Big Data se presentan como una gran ventaja en el procesamiento de los datos. En general, los estadísticos son una forma acertada y necesaria tanto para un exploración de datos que te guie en los cuestionamientos clave, como para la instancia de análisis y visualización de la información.
Por esta razón, un data scientist debe contar con los conocimientos necesarios relacionados con estas alternativas para potenciar los resultados arrojados al elegir la mejor de solución para un estudio de los datos. Es así como, por medio de estas herramientas, podrás desempeñarte efectivamente en el trabajo estadístico del Big Data.
Dado lo fundamentales que resultan estas bases y sus implicaciones en la toma de decisiones, en este post te explicamos qué es y cómo funciona la desigualdad de Chebyshev en estadística Big Data.
¿Qué es desigualdad de Chebyshev en estadística Big Data?
La desigualdad de Chebyshev en estadística Big Data es un cálculo estadístico en el que se ofrece una cota superior a la probabilidad del valor de x variable aleatoria con varianza finita que se encuentra cercana a su respectiva esperanza matemática, es decir, la media de la variable aleatoria.
Además, este tipo de estimación cuenta con un intervalo de confianza alto, puesto que cuenta con una gran probabilidad de que los resultados arrojados sean certeros. La desigualdad de Chebyshev en estadística Big Data, en su fórmula se presenta de la siguiente forma:
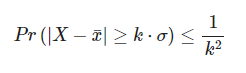
K representa las desviaciones típicas y X el valor estimado. Dicho en otras palabras, la probabilidad de que haya valores fuera del intervalo [x¯−kσ,x¯+kσ] es menor o igual a 1/k2.
Por otra parte, la desigualdad de Chebyshev en estadística Big Data es un límite muy pesimista, a partir de la que se pueden obtener mejores resultados cuando la distribución es conocida.
Ejemplo de alturas
Ahora, por medio de un ejemplo práctico, te ilustramos cómo se desarrolla la desigualdad de Chebyshev en estadística Big Data, de manera que puedas ensayar las fórmulas y comprender sus resultados.
Entonces, empezamos con el vector de alturas a partir del que se puede sacar una tabla en función de k. De esta forma, se puede decir que, como máximo, el 44% que en datos sería 11.52=0.4444.
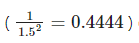
Así que de las muestras que se encuentran fuera del intervalo:
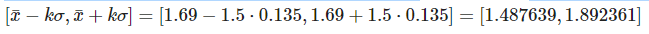
Se pretende realizar el siguiente análisis:
k <- c(1.01,seq(from=1.5, to=5, by=0.5))
margen <- data.frame(limite_inf=mean(alturas)-k*sd(alturas),
limite_sup=mean(alturas)+k*sd(alturas),
prob = 1/k^2,
k
)
margen
plot(margen$k,margen$prob,t='l',xlab="k",ylab="Probabilidad",main="Desigualdad de Chebyshev") grid()
plot(margen$limite_sup-margen$limite_inf,margen$prob,t='l',
xlab="Tamaño del margen",
ylab="Probabilidad",main="Desigualdad de Chebyshev")
grid()
En el desarrollo de este post te hemos familiarizado con todo lo relacionado a la desigualdad de Chebyshev en estadística Big Data. Ahora, podrás implementar este tipo de cálculo que te facilitará la certeza de los resultados acertados. Sin embargo, la estadística cuenta con muchas más herramientas que te servirán para otro tipo de operaciones, ¡por lo que debes seguir aprendiendo sobre el Big Data!
Si aún no sabes cómo, en KeepCoding te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Por medio de este, se te presentarán las teorías de aprendizaje automático con énfasis en algoritmos de regresión y clasificación. De manera que, con el tiempo, serás capaz de conocer las ventajas y desventajas de los distintos algoritmos analizados. Además, adquirirás experiencia gracias a que se fusionan los fundamentos teóricos con ejemplos prácticos y realistas para que puedas aplicarlos. ¡Pide información, inscríbete ahora y sigue aprendiendo!



