La distribución chi-cuadrado en estadística Big Data forma parte de la serie de distribuciones continuas utilizadas para el desarrollo de ciertos análisis estadísticos. Junto a esta, también podrás contar con las distribuciones uniforme, gaussiana y exponencial; evidentemente, cada una de ellas se dedica a un determinado tipo de datos y dependen de lo que se quiera conseguir en el estudio estadístico. Ahora, si lo que buscas es conocer más sobre la distribución chi-cuadrado en estadística Big Data, ¡este post es ideal para ti!
Este tipo de opciones para conseguir llevar a cabo a un análisis de probabilidad, además, son parte de los primeros acercamientos de un data scientist para investigar a los macrodatos y sus posibilidad. Por esta razón, en este artículo, te explicamos qué es y cómo funciona la distribución chi-cuadrado en estadística Big Data.
¿Qué es una distribución en estadística?
Antes de entrar en materia con la distribución chi-cuadrado en estadística Big Data, te recordamos a qué hace referencia una distribución y cuáles son sus variantes.
En primera instancia, una distribución forma parte de las funciones de probabilidad conocidas, es decir, las que aparecen con mayor frecuencia cuando se realiza algún tipo de estudio estadístico, por ello, podrás contar con dos grandes grupos: las distribuciones continuas y las discretas.
Por otra parte, una distribución, independientemente de su carácter, es una propiedad en la que, por ejemplo, se supone que f(x) es la función de densidad de la probabilidad de una variable aleatoria x que se encuentra en los datos estudiados.
Su integral, es decir, la suma a lo largo de todo el dominio, es igual a 1. Esto significa que la suma de probabilidades de todos los posibles valores será 1. Ahora, como chi-cuadrado forma parte de las distribuciones continuas, te compartimos cómo se fórmula para estas:
- Para una distribución continua la inscripción será:
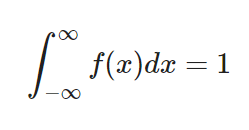
Por otra parte, su integral (la suma), a lo largo de los dos puntos [a, b], da la probabilidad de que la variable aleatoria x caiga en ese rango.
- Para una distribución continua la fórmula será:
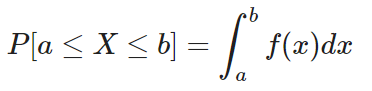
Distribución chi-cuadrado en estadística Big Data
La función de distribución chi-cuadrado en estadística Big Data cuenta con k grados de libertad que aparecen al sumar el cuadrado de k variables que siguen a variables gaussianas independientes.
Por otra parte, su principal característica es que se usa para los tests estadísticos de probabilidad. En cuanto a su implementación en el estudio, a continuación te compartimos cuál es su función de distribución:

Funciones en R
Ahora, a partir de ella, podrás emplear ciertas funciones en R, el lenguaje de programación predilecto para estadística en el manejo Big Data.
A continuación, te presentamos cuáles son las funciones en R para la distribución chi-cuadrado en estadística Big Data:
- dchisq(x, df, ncp = 0): te ofrece la probabilidad de P(X=x).
- pchisq(q, df, ncp = 0): te dará la probabilidad de P(Xx)=p.
- rchisq(n, df, ncp = 0): esta genera un vector aleatorio de la dimensión n.
Por último, debes tener en cuenta que df es el número de grados de libertad en la distribución.
Sigue aprendiendo sobre el Big Data
En este post, te hemos presentado todo lo relacionado con la distribución chi-cuadrado en estadística Big Data, con el fin de que puedas conocer más sobre ella y saber para qué sirve en tu procesamiento de los macrodatos. Sin embargo, recuerda que también puedes contar con otro tipo de distribuciones continuas y discretas; su uso dependerá del interés del análisis estadístico.
Si requieres más ayuda para seguir aprendiendo sobre el Big Data, en KeepCoding te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning con el propósito de ayudarte en este proceso de aprendizaje. Por medio de esta formación íntegra e intensiva, podrás aprenderlo todo, tanto de forma teórica como práctica, sobre los principales sistemas y lenguajes de programación que se encargan del procesamiento de un gran volumen de datos. Además, podrás estudiar acompañado de grandes profesionales para convertirte en todo un experto en el área. ¡Apúntate ahora!











