La distribución de Poisson en estadística Big Data es una de las distribuciones discretas utilizadas durante un estudio estadístico de los macrodatos. En específico, esta distribución destaca porque logra la generalización de Binomial cuando hay infinitos eventos de probabilidad muy baja.
Por esta razón y muchas otras ventajas más con las que cuenta, en este post te explicamos qué es y cómo funciona la distribución de Poisson en estadística Big Data.
Distribución de Poisson en estadística Big Data
La distribución de Poisson en estadística Big Data tiene su origen en una distribución binomial en la medida en que n -> ∞ y p -> 0, manteniendo λ = n · p constante. De manera que expresa la probabilidad de que un número de eventos dado ocurra en un intervalo de tiempo (o espacio) fijo o si los eventos ocurren con una frecuencia constante y son independientes (no dependen de cuándo ocurrió el último evento).
Por ejemplo: averiguar el número de llamadas que recibe una antena de telefonía móvil en una franja horaria.
Sus estimadores de media y varianza se representan así:
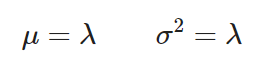
Función de densidad de probabilidad
Un evento puede ocurrir K veces en un intervalo de tiempo dado:
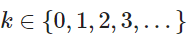
El número de eventos que ocurre en media se define con λ. La probabilidad de observar eventos en un intervalo viene dado por la siguiente ecuación:
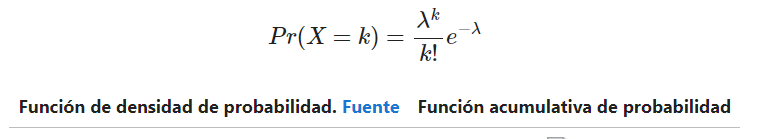
Para valores grandes de λ, en torno a λ = 100, la distribución de Poisson en estadística Big Data tiende a una gaussiana de media μ = λ y desviación típica:
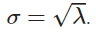
Por ejemplo: imagina que tienes un call center que recibe de media 2 llamadas por minuto.
¿Cuál es la probabilidad de recibir exactamente 5 llamadas en un minuto?
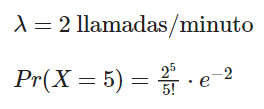
k=5
l=2
print(paste("METODO 1: La probabilidad de recibir exactamente",
k,"llamadas en un minuto es:",l^k/factorial(k)*exp(-2)))
print(paste("METODO 2: La probabilidad de recibir exactamente",
k,"llamadas en un minuto es:",dpois(k,l)))
[1] «MÉTODO 1: la probabilidad de recibir exactamente 5 llamadas en un minuto es: 0.0360894088630967»
[1] «MÉTODO 2: la probabilidad de recibir exactamente 5 llamadas en un minuto es: 0.0360894088630967»
¿Cuál es la probabilidad de recibir 5 o más llamadas en un minuto?
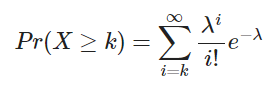
Lo que es equivalente a:
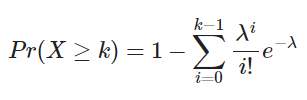
k<-5
l<-2
p<-0
for (i in k:100){
p<-p+dpois(i,l)
}
print(paste("METODO 1: La probabilidad de recibir más de",k,"llamadas en un minuto es:",p))
p<-1
for (i in 0:(k-1)){
p<- p-dpois(i,l)
}
print(paste("METODO 2: La probabilidad de recibir más de",k,"llamadas en un minuto es:",p))
p<-1-ppois(k-1,l)
print(paste("METODO 3: La probabilidad de recibir más de",k,"llamadas en un minuto es:",p))
[1] «MÉTODO 1: La probabilidad de recibir más de 5 llamadas en un minuto es: 0.0526530173437111»
[1] «MÉTODO 2: La probabilidad de recibir más de 5 llamadas en un minuto es: 0.0526530173437111»
[1] «MÉTODO 3: La probabilidad de recibir más de 5 llamadas en un minuto es: 0.0526530173437111»
Funciones en R
Podemos generar una variable aleatoria que siga una distribución de Poisson mediante la función rpois().
Por ejemplo, si queremos generar 10000 muestras de varias distribuciones de Poisson con medias 2, 4 y 20 basta con ejecutar:
l<-c(2,4,20) numSamples<-10000 myPoissonDataVector<-rpois(numSamples*length(l),l) length(myPoissonDataVector)
30000
head(rep(l,numSamples),10)
- 2
- 4
- 20
- 2
- 4
- 20
- 2
- 4
- 20
- 2
myPoissonDataFrame<-data.frame(val=myPoissonDataVector,lambda=rep(l,numSamples)) myPoissonDataFrame$lambda<-factor(myPoissonDataFrame$lambda) head(myPoissonDataFrame)
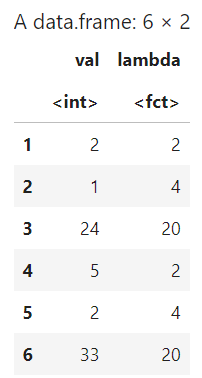
require(ggplot2) ggplot(data=myPoissonDataFrame, aes(x=val,colour=lambda)) + geom_histogram(position="dodge",bins=30)+ geom_density(bw=1)+ geom_vline(xintercept=3.65,color="blue")
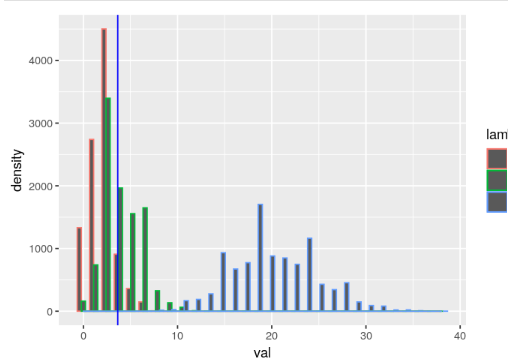
Podrás comprobar como una distribución binomial a medida que n -> ∞ y p -> 0, manteniendo λ = n·p constante, converge a una distribución de Poisson en estadística Big Data con media λ.
l<-4
n<-c(5,10,100)
p<-l/n
numSamples<-10000
myBinomialDataVector<-rbinom(numSamples*length(n),size=n,prob=p)
myPoissonDataFrame<-data.frame(val=myBinomialDataVector,n=rep(n,numSamples))
myPoissonDataFrame$n<-factor(myPoissonDataFrame$n)
require(ggplot2)
ggplot(data=myPoissonDataFrame, aes(x=val,colour=n)) +geom_histogram(position="dodge",bins=30)+
stat_function(fun=function(x,...){dpois(round(x),...)*10000},args = list(lambda = l),
geom="area",color="#a98600",fill="yellow",alpha=0.3)
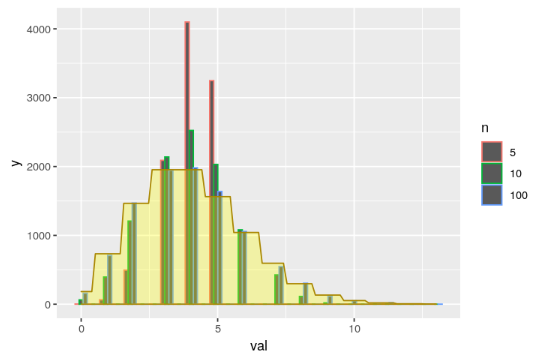
En este post te hemos explicado cómo funciona la distribución de Poisson en estadística Big Data, sin embargo, te aconsejamos conocer los demás tipos de distribuciones para que elijas la que mejor funcione con tus datos procesados. Ahora, si no sabes cómo instruirte sobre este y otros temas del manejo Big Data, ¡te traemos una gran opción!
Conoce nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Gracias a esta formación, conocerás más herramientas, como puede ser Tableau Desktop, mediante ejercicios prácticos para aprender a usar las diferentes conexiones, filtrados, tipos de datos, análisis estadísticos, formulación, creación de dashboards, historias, etc. ¡Empieza ahora y conviértete en un experto del sector IT en pocos meses!



