En este artículo veremos un ejemplo del compromiso sesgo-varianza. Recordemos que el compromiso sesgo-varianza es un principio que nos permite analizar el alcance de las prestaciones en tareas de aprendizaje supervisado.

Ejemplo de compromiso sesgo-varianza

Veamos un ejemplo del compromiso sesgo-varianza. Supongamos que y = g (x) + ε, donde:

g(x) = cos (1.5 πx), x ε [0,1]

Como esto es un ejemplo, la función anterior no la vamos a tener en un caso de la vida real, porque si la tuviéramos, no tendríamos que estar haciendo machine learning.

De todos modos, en este ejemplo del compromiso sesgo-varianza la pondremos para que veamos, al final, cómo queda y si coincide nuestro resultado con la función planteada en este inicio.

ε ~ N (0, σ²), σ = 0.2
Disponemos del conjunto de datos D = {x⁽ⁱ⁾ , y⁽ⁱ⁾}, con i = 1, … , N

Queremos estimar g(x) (como si no lo conociéramos) a partir del conjunto de datos D disponible. Para ello, vamos a utilizar tres funciones:

Regresión lineal orden 1: modelo sencillo, que es una recta.

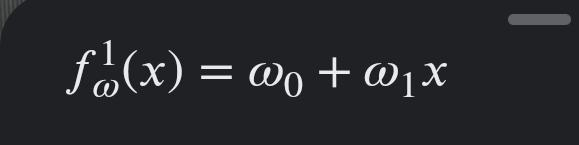
Regresión lineal orden 4: modelo intermedio, de factores polinomios.

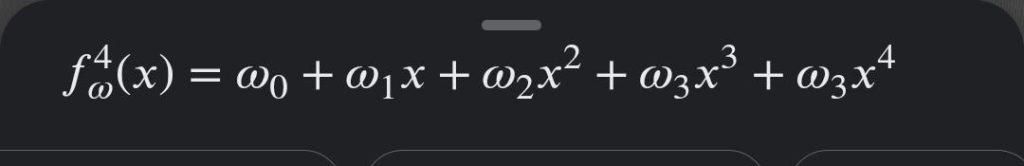
Regresión lineal orden 7: modelo flexible (complejo).

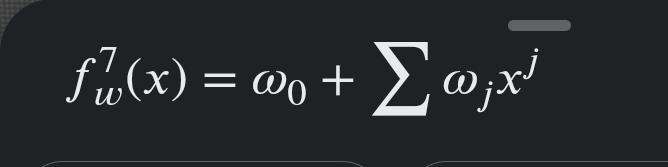
¿Te atreves a generar una hipótesis de cómo será el sesgo-varianza de los resultados del conjunto de datos de cada una de las funciones?

Mientras piensas, comencemos con el ejercicio del compromiso sesgo-varianza. Primero, dibujemos la función g(x) y el conjunto de datos D = {x⁽ⁱ⁾ , y⁽ⁱ⁾}.

#Ejemplo de compromiso sesgo-varianza
N_train = 10
N_test =100

#función verdadera g(x)
x = np.linspace (0, 1, N_test)
g_x = np.cos (1.5 * np.pi * x)

# proceso y
np.random.seed (0) # para asegurar reproducibilidad
epsilon = np.random.randn (N_test) * 0.2
y = g_x + epsilon

# Datos: D = (x_i, y_i, obtenemos una muestra
idx = np.random.randint (0, N_test, N_train)
x_i = x [idx]
y_i = y [idx]

#Ejemplo de compromiso sesgo-varianza
#YOUR CODE HERE: dibuje la función g(x), y el conjunto de datos x_i, y_i
##########
plt.plot (x, g_x, 'r', label = 'g (x)')
plt.plot (x_i, y_i, 'b.', label = 'y')
plt.legend ()
plt.show ()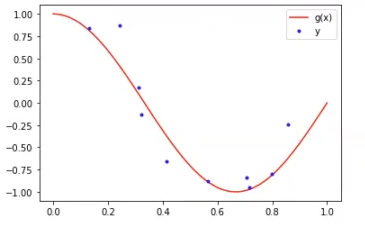

Aquí tenemos la función real. En la vida real, lo que se nos presentará en nuestro ejemplo de compromiso sesgo-varianza es una serie de datos que siguen una distribución desconocida y lo que queremos es algo que se ajuste a dicha distribución a partir de los datos que tengamos.

A continuación, representamos la salida obtenida y el error cometido para las tres funciones definidas:

#Ejemplo de compromiso sesgo-varianza
#Ejecute esta celda
grado_polinomio = [1, 3, 7]

#idx = np.random.randint (0, N_test, N_train)
#x_i = x [idx]
#y_i = y [idx]

plt.figure (figsize = (14, 5))
for j, d in enumerate (grado_polinomio):

fk, mse, miRegresionLineal (x_i, y_i, x, y, d)

#Ejemplo de compromiso sesgo-varianza
ax = plt.subplot (1, 3, j + 1)
plt.setp (ax, xticks = (), yticks = ())
plt.plot (x, g_x, 'r', label = '$g (x) $')
plt.plot (x_i, y_i, 'b.', label = 'muestras')
plt.plot (x, f_k, 'g', label = '$f_w (x) $')
plt.title ('Grado: %i\nMSE:%.2f' % (d, mse))
plt.legend ()
plt.xlim ((0, 1))
plt.ylim ((-2, 2))

plt.show()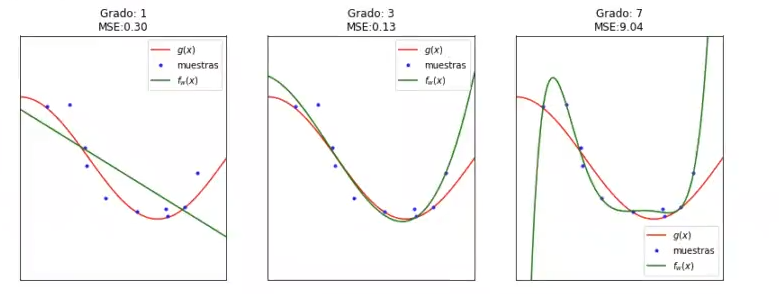

Lo que podemos observar es que la gráfica de Grado 3 está bastante bien ajustada.

En la gráfica de Grado 1 se ve justamente lo que esperábamos: una recta, ya que esto es lo que nos debe arrojar una regresión lineal de grado simple.

Vemos también que la gráfica de Grado 3 tiene un error cuadrático medio (MSE) de 0.13, que es menos de la mitad del MSE de la gráfica de Grado 1.

Podríamos decir que, a medida que volvemos el modelo más complejo, mejora; en vez de grado 3 podemos meterle grado 30, pero, como siempre decimos, no todo es tan simple como parece.

Lo que sucede aquí, en la gráfica de Grado 7, es que la reducción del sesgo la estamos metiendo en una excelente varianza, pero dependemos completamente de nuestros datos de entrenamiento y, en el momento en que llega una instancia nueva, quedamos fuera.

Esto podemos corroborarlo al mirar el error cuadrático medio de la gráfica de Grado 7: 9.04, que es altísimo si lo comparamos con los otros dos MSE.

Se puede comprobar que, en el ejemplo de compromiso sesgo-varianza, el modelo de orden 7 se sobreajusta a los datos de entrenamiento (la función pasa por los puntos de entrenamiento) y, por tanto, su capacidad de generalización es muy limitada.

Ahora que sabemos cómo funciona y hemos visto un ejemplo de compromiso sesgo-varianza, podemos seguir aprendiendo sobre Big Data. Para ello, en KeepCoding tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todas las herramientas y conocimiento teórico y práctico para seguir tu camino y alcanzar el éxito en este sector. ¡Anímate a transformar tu futuro y solicita ahora más información!