En este artículo veremos un ejemplo de distribución exponencial en R utilizando un dataset de accidentes de tráfico con datos desde el 2009 hasta 2016.
Desarrollo de ejemplo de distribución exponencial en R
accidentes <- read.csv ('data//Accidentes_Madrid.csv')
head (accidentes)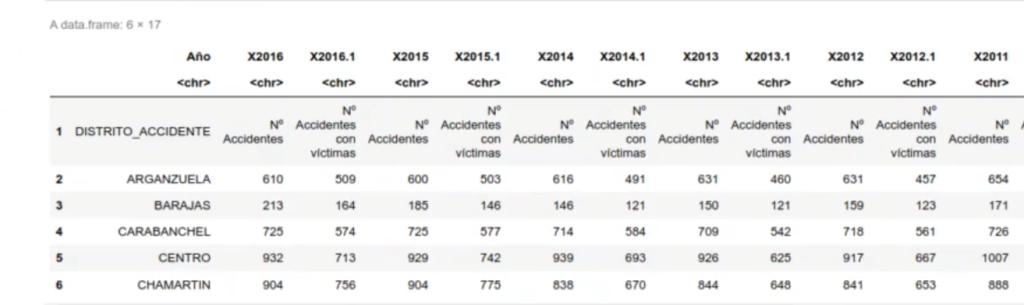
acc_tmp <- t (accidentes)
acc_tmp [1 ,]
nrow (acc_tmp [2 : nrow (acc_tmp), ])16
accidentes_ t = data.frame (acc_tmp [2 : nrow (acc_tmp), 1)
colnames (accidentes_t) <- c ("tipo", acc_tmp [1, 2 : ncol (acc_tmp)])
accidentes_t$anyo <- as.numeric (substr (rownanes (accidentes_t), 2, 6))
rownames (accidentes_t) <- NULL
library (plyr)
accidentes t$tipo <- revalue (accidentes_t$tipo,
c ("No Accidentes" = "Total", "No Accidentes con victimas" = "victimas"))
head (accidentes_t)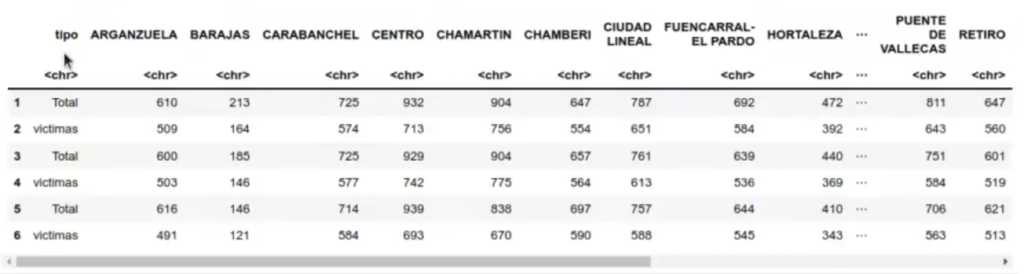
library (reshape2)
library (dplyr)
df_acc <- melt (data = accidentes_t, id.vars = c ("anyo", "tipo"))
df_acc$value <- as.numeric (df_acc$value)
df_acc <- df_acc %>% dplyr :: rename (distrito = variable)
df_acc$distrito = factor (trimws (df_acc$distrito))
head (df_acc)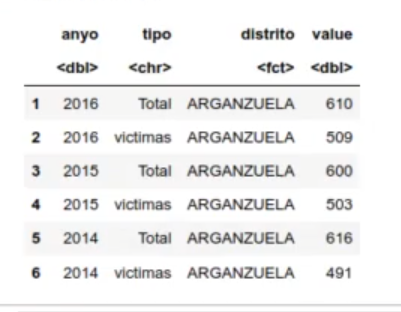
df_acc_total <- df_acc [df_acc$tipo == "Total", ]
df_acc_total <- df_acc_total %>% dplyr :: rename (Total = value) %>% select (-tipo)
df_acc_victimas <- df_acc [df_accstipo == "victimas", ]
df_acc_victimas <- df_acc_victimas %>% dplyr :: rename (victimas = value) %>% select (-tipo)
df_acc <- merge (df_acc_total, df_acc_victimas, by = c ("anyo", "distrito"))
str(df_acc)
library (ggplot2)
ggplot (df_acc, aes (x = anyo, y = victimas)) + geom_point () + geom_smooth ()‘geom_smooth()’ using method = ‘loess’ and formula ‘y ~ x’
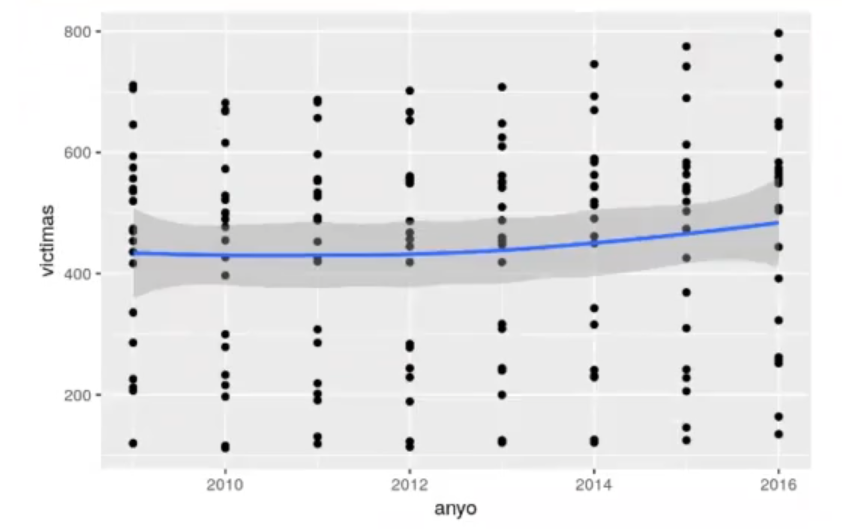
Modelo GL
Para este ejemplo de distribución exponencial en R vamos a crear un modelo GLM basado en Poisson y otro en el tradicional Gauss. Estos modelos tratarán de predecir el número medio de víctimas que hay en función del año para todos los distritos. Más adelante realizaremos una separación por distrito, pero por ahora ignoraremos la columna distrito.
Como veremos, el AIC es mayor en el modelo gaussiano que en el de Poisson, lo que significa que la verosimilitud (likelihood) es mayor en la del modelo de Poisson.
model_accidente <- glm (df_acc, formula = "victimas ~ anyo", family = poisson)
summary (model_accidente)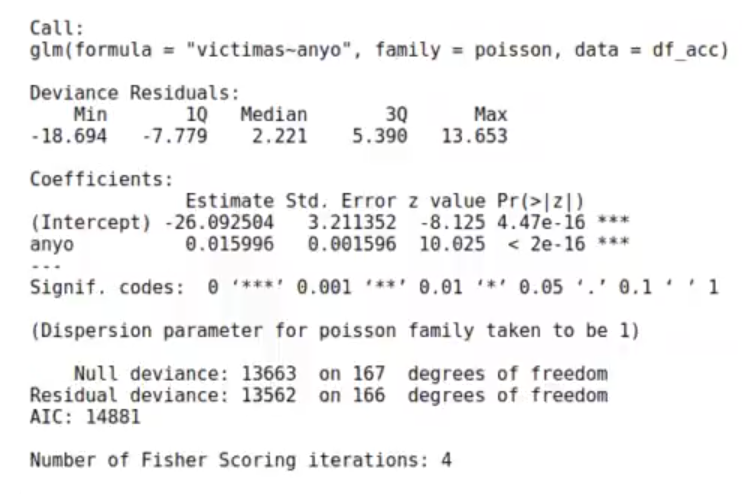
model_accidente_gauss <- glm(df_acc, formula = victimas ~ anyo, family = gaussian)
summary (model_accidente_gauss)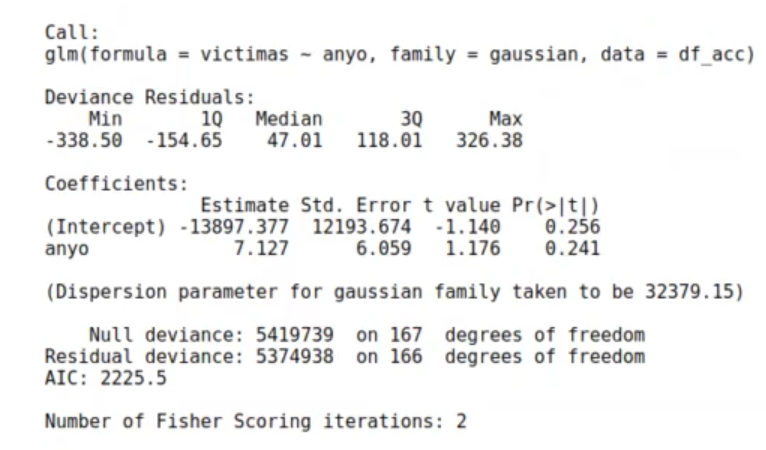
df_acc$pred_poisson <- exp (predict (model_accidente, df_acc)) #df_accspred poisson <- predict (model_accidente, df_acc, type = "response")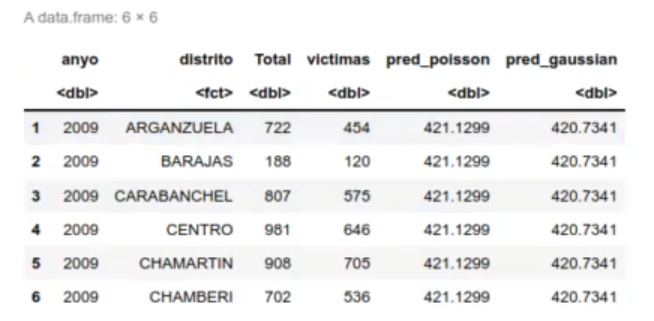
confint (model_accidente)
confint (model_accidente_gauss)Waiting for profiling to be done…
| 2.5 % | 97.5 % | |
| (Intercept) | -32.3870474 | -19.79869517 |
| anyo | 0.0128685 | 0.01612332 |
Waiting for profiling to be done…
| 2.5 % | 97.5 % | |
| (Intercept) | -37796.538893 | 10001.78492 |
| anyo | -4.748368 | 19.00234 |
Siguiendo con el ejemplo de distribución exponencial en R, si pintamos los dos modelos veremos que las líneas de la regresión son prácticamente idénticas:
options (repr.plot.height = 4, repr.plot.width = 6)
library (ggplot2)
ggplot (df_acc, aes (x = anyo, y = victimas)) + geom_point () +
geom_line (aes (y = pred_poisson), color = "red") + geom_line (aes (y = pred_gaussian), color = "blue")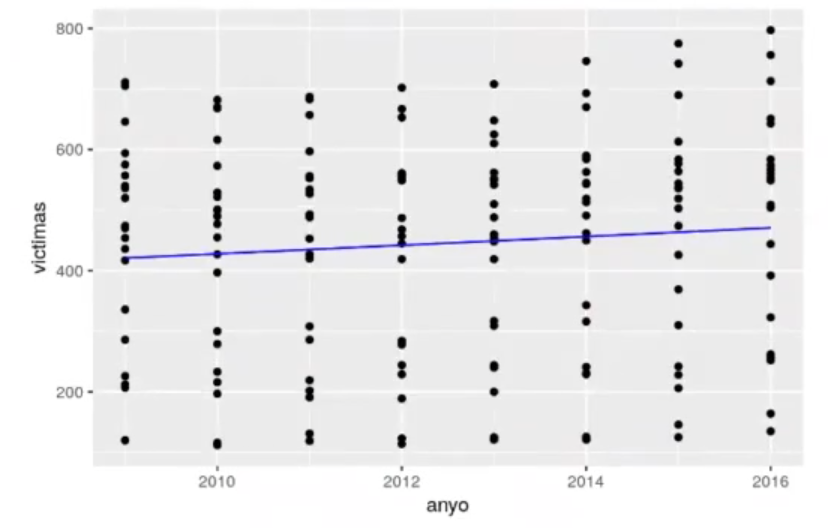
En este ejemplo de distribución exponencial en R, si comprobamos la diferencia de un año respecto al siguiente en la predicción gaussiana, vemos que la diferencia es constante. Todos los años el número de víctimas aumenta de forma lineal en 7.127, lo que corresponde con el coeficiente. Para este caso, la formula de la predicción es:
víctimas = -13897.377 + anyo * 7.127
En cambio, la regresión de Poisson nos dice que el número medio de víctimas esperado cada año en un distrito es:
víctimas = exp (-26.092504 + anyo * 0.015996)
víctimas = exp (-26.092504) * exp (anyo * 0.015996)
víctimas = 4.657-10-12 * exp (anyo * 0.015996)
Esto significa que cada año que pasa el número de víctimas aumenta de forma geométrica e0.015996 = 1.016124. Es decir, cada año los accidentes aumentan un 1.6 %.
¿Qué sigue?
Ahora que hemos entendido este ejemplo de distribución exponencial en R, ¿qué te parece si seguimos aprendiendo? Para ello ponemos a tu disposición el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el cual podrás, en poco tiempo, incursionar en el mercado labora. ¡Anímate a impulsar tu carrera y solicita más información!











