En este post veremos un ejemplo de sistemas de ecuaciones lineales.
¿Conoces cuál es el típico juego que te aparece en Facebook de calcular el valor de distintos objetos?
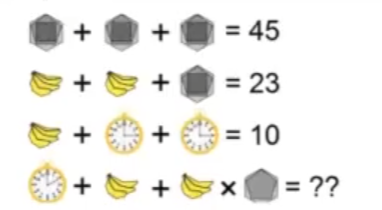
Pues bien, todos ellos se resuelven siempre de la misma forma: usando un sistema de ecuaciones lineales. Así que vamos a intentar resolver uno de ellos a través de un ejemplo de sistemas de ecuaciones lineales para que entiendas mejor el concepto.
Ejemplo de sistemas de ecuaciones lineales
Imagina que tres campesinos se encontraron en el mercado ganadero:
—Mira —le dijo Luis a Juan—, te daré 6 de mis cerdos por 1 de tus caballos y así tendrás el doble de animales que yo.
—Si ese es tu modo de hacer negocios —le respondió Pepe a Luis—, te daré 14 ovejas por 1 caballo, y entonces tendrás el triple de animales que yo.
—Bien —le dijo Juan a Pepe—. Te daré 4 vacas por un caballo y entonces tendrás seis veces más animales que yo.
¿Cuántos animales llevaron al mercado Juan, Luis y Pepe?
Llamemos L al número de animales que tiene Luis, J al número de animales que posee Juan y P al número de animales que le pertenecen a Pepe. Si analizamos el párrafo y lo convertimos en ecuaciones, nos quedaría algo así:
J – 1 + 6 = 2 . (L – 6 + 1)
L – 1 + 14 = 3 . (P – 14 + 1)
P + 4 – 1 = 6 . (J + 1 – 4)
De modo que la primera expresión estaría relacionando el enunciado de Luis, es decir, el primer enunciado; la segunda expresión concordaría con el segundo enunciado, es decir, con el de Pepe; y el tercer enunciado, dicho por Juan, correspondería a la tercera expresión.
Hasta el momento solo hemos traducido lo que han dicho Luis, Pepe y Juan. Esto no es realmente lo importante; lo importante viene cuando reagrupamos dichas expresiones. Veamos:
J – 2L = -15
L – 3P = -52
P – 6J = -21
Observemos cómo resolverlo usando Numpy:
#Ejemplo de sistemas de ecuaciones lineales
import numpy as np
# J, L, P
A = np.array ([[1, -2, 0],
[0, 1, -3],
[-6, 0, 1]])
print ("Determinante: ", np.linalg.det (A))Determinante: -35.00000000000001
Como el determinante es diferente a 0, tenemos una única solución, que buscaremos con linalg:
#Ejemplo de sistemas de ecuaciones lineales
X = np.linalg.solve (A, B)
print (X)[[7.]
[11.]
[21.]]
J – 1 + 6 = 2L – 12 + 2
J + 5 = 2L – 10
J – 2 * L = -15
Ahora que has descubierto cómo resolver este ejemplo de sistemas de ecuaciones lineales, puedes seguir formándote en el mundo del Big Data para convertirte en un experto en el sector. Si deseas acceder a una de las disciplinas más demandadas y con mejores sueldos del mundo laboral, no puedes perderte el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación íntegra e intensiva con la que adquirirás, en muy pocos meses, todos los conocimientos que te ayudarán a lograr el trabajo de tus sueños. ¡Entra ya para solicitar información y da el paso que transformará tu futuro!











