Ejemplo de una neurona en Deep Learning

Si tenemos en cuenta que normalmente cualquier problema que se os ocurra puede ser descompuesto y modelado en forma de funciones matemáticas, considerar un ejemplo de una neurona en Deep Learning es de suma importancia. Esto se debe a que, de acuerdo con este teorema, una red neuronal en Deep Learning debería ser capaz de resolver cualquier problema. A partir de ello, se convierte en algo esencial realizar una práctica en los análisis que se pueden desarrollar a partir de esta.

Por esta razón, en el desarrollo de este post, te exponemos un breve ejemplo de una neurona en Deep Learning, a partir de la implementación de gradient descent o gradiente descendente como parte del procesamiento de los datos.

Ejemplo de una neurona en Deep Learning

Pues bien, conocer cómo se presenta una neurona se comprende mucho mejor si se aprende implementándolo, por ello, te presentamos este ejemplo de una neurona en Deep Learning para ver cómo se implementa con TensorFlow.

# implementación de gradient descent en una red neuronal
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np

# Implementamos nuestra función de activación: la función logística
def sigmoid_activation(x):
  return 1.0 / (1 + np.exp(-x))

# Implementamos la función que nos calcula las predicciones (Forward pass)
def predict(X,W):
  preds = sigmoid_activation(X.dot(W))
  # preds devuelve una probabilidad para cada posible clase, cuya suma da 1
  # necesitamos pasar este vector de probabilidades a un vector de clases:
  # umbralizamos
  preds[preds <= 0.5] = 0
  preds[preds > 0.5] = 1
  
  #Devolvemos las predicciones
  return preds

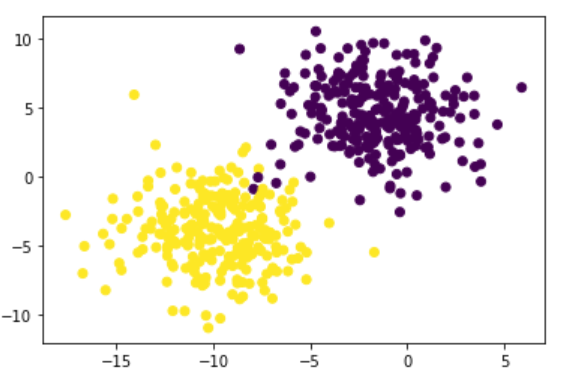
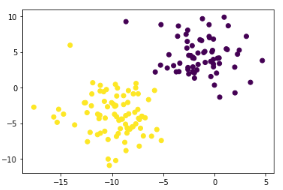
# Generamos un dataset de juguete
(X, y) = make_blobs(n_samples=500, n_features=2, centers=2, cluster_std=2.5, random_state=1)
y = y.reshape((y.shape[0], 1))

# Lo visualizamos
plt.scatter(X[:, 0], X[:, 1], c=y[:, 0])

<matplotlib.collections.PathCollection at 0x7f008b8249b0>

# Shape de X
X.shape

(500, 2)

# Incluimos la columna de bias para poder realizar los cálculos de forma 
# eficiente (bias trick)
X = np.c_[X, np.ones((X.shape[0]))]

# Veamos las dimensiones de X
X.shape

(500, 3)

# Partimos en training y testing
(train_X, test_X, train_Y, test_Y) = train_test_split(X, y, test_size=0.3, random_state=1)

# Veamos los tamaños
train_X.shape

(350, 3)

train_Y.shape

(350, 1)

test_X.shape

(150, 3)

test_Y.shape

(150, 1)

# Inicializamos nuestra matriz de pesos de forma aleatoria y el vector de 
# históricos de pérdidas
W = np.random.randn(X.shape[1], 1)
losses = []
print(W)

[[-0.96418793]
[-0.53384948]
[ 0.7176862 ]]

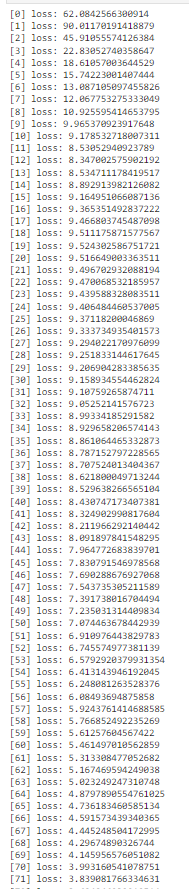
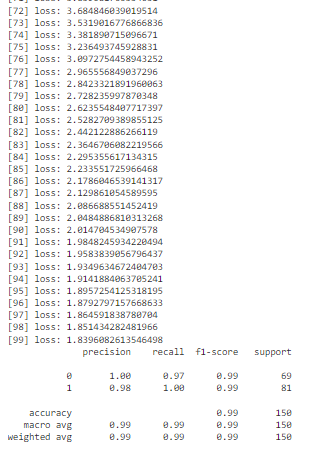
# Empezamos con el FORWARD PROPAGATION

# Este es un proceso iterativo en el que poco a poco se van 
# actualizando los pesos usando el gradient descent para llegar a una mejor
# solución => épocas

n_epochs = 100
for epoch in np.arange(0, n_epochs):

  # calculamos las predicciones que da nuestra red con sus pesos actuales
  preds = sigmoid_activation(train_X.dot(W))

  # calculamos el error con respecto a las etiquetas
  error = preds - train_Y

  # definimos la función de pérdidas: en este caso, el error cuadrático
  # hay una gran variedad de funciones de pérdidas distintas que iremos viendo
  loss = np.sum(error ** 2)

  # añadimos nuestra pérdida al vector histórico de pérdidas
  losses.append(loss)

  # y comenzamos con el BACK PROPAGATION
  gradient = train_X.T.dot(error)

  # ahora actualizamos nuestros pesos
  # pero primero definimos nuestro learning rate
  learning_rate = 0.01
  W += -learning_rate * gradient
  
  # escribimos en pantalla cómo va el asunto
  print("[{}] loss: {}".format(epoch, loss))

  # en cuanto acaba de entrenar, vemos lo que ha estudiado nuestra red
preds = predict(test_X, W)
print(classification_report(test_Y, preds))

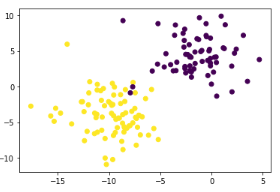
# y ahora algo que os recomiendo que hagáis siempre que podáis, comprobar 
# vuestras entradas, las predicciones y la curva de pérdidas
plt.scatter(test_X[:, 0], test_X[:, 1], c=test_Y[:,0])

<matplotlib.collections.PathCollection at 0x7f0088b0c748>

# veámoslo ahora con las predicciones
plt.scatter(test_X[:, 0], test_X[:, 1], c=preds[:,0])

<matplotlib.collections.PathCollection at 0x7f0088a68e48>

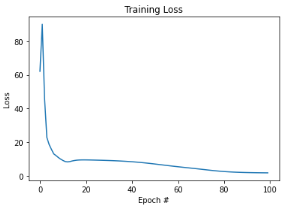
# veamos nuestra curva de pérdidas
plt.plot(np.arange(0, n_epochs), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")

Text(0, 0.5, 'Loss')

En este post, te has podido relacionar con un breve ejemplo de una neurona en Deep Learning. Recuerda que debes apropiar este tipo de cálculos y desarrollo de redes neuronales a los datos que te encuentres trabajando y que, cada uno de estos, estará guiado por los resultados esperados para el procesamiento de los macrodatos.

Por otra parte, desde KeepCodging te traemos el Bootcamp Full Stack Big Data, gracias al que podrás aprender mucho más sobre este servicio de Google y, en general, sobre los sistemas y herramientas más importantes en el universo del Big Data. De la mano de profesionales y en menos de nueve meses, te podrás convertir en todo un experto y conocer e identificar las alternativas de gestión de datos más apropiadas para los estudios de los macrodatos. ¿A qué estás esperando para empezar? ¡Inscríbete ahora!