¿Alguna vez has escuchado mencionar la sigla SVM? Esta corresponde a support vector machines o, en español, maquinas de vectores de soporte.
Las SVM inicialmente fueron concebidas para solucionar problemas de clasificación y, posteriormente, fueron extendidas a regresión, pero sigue siendo la clasificación el campo en el que más se usan. De modo que la siglas para cada una de estas son:
- SVC: Support Vector Classification.
- SVR: Support Vector Regression.
Las SVM se definen, entonces, como clasificadores lineales de máximo margen. Fueron propuestas a finales de los años 90, aunque tuvieron su auge en los 2000, ya que, entre otras cosas, proporcionaban:
- Grandes prestaciones en aprendizaje supervisado.
- Métodos kernel.
Los métodos kernel, sumados con las SVM, son el enfoque más recomendado y óptimo para provocar un verdadero impacto en nuestros ejercicios de clasificación.
Intuición
Tenemos un clasificador lineal definido por un hiperplano separador de máximo margen:
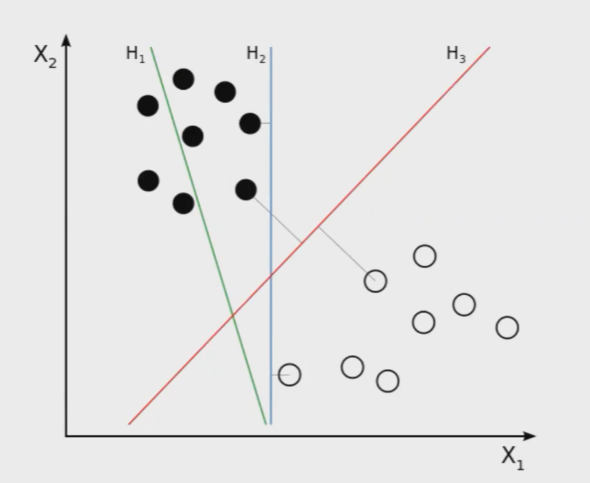
Esta división está hecha del siguiente modo: los círculos negros a un lado y los blancos al otro. Como podemos observar, este es un problema linealmente separable. Tenemos tres clasificadores lineales aquí representados: el verde, el azul y el rojo. El verde es el peor, ya que, aun teniendo una distribución sencilla y una clasificación perfectamente separable, este clasificador no hace bien su trabajo.
Tanto el azul como el rojo son clasificadores perfectos, sin embargo, hay uno que es mejor, ¿adivinas cuál es?
La respuesta correcta es el rojo. De manera intuitiva, podemos identificar que el rojo es el indicado porque va a generalizar mejor. Esto se debe a que está dejando más espacio entre los elementos de ambos grupos. Entonces, si tenemos una instancia blanca (de puntos blancos) nueva, da igual que el rojo esté pegado, porque si tenemos la instancia nueva en algún espacio del conjunto de puntos blancos, el clasificador rojo nos la va a clasificar bien igualmente.
En conclusión, tener una distancia mayor nos va a permitir tener una mejor generalización, porque las nuevas instancias que lleguen van a tener más distancia para clasificarse en uno u otro punto.
Estas son rectas porque aquí estamos resolviendo un problema en dos dimensiones, pero SVM no funciona solo con planos de dos dimensiones, sino con tres también. En este caso, lo que va a hacer es un plano; si son más de tres dimensiones vamos a hacer un hiperplano.
Plano separador
Observemos el plano separador de los SVM:
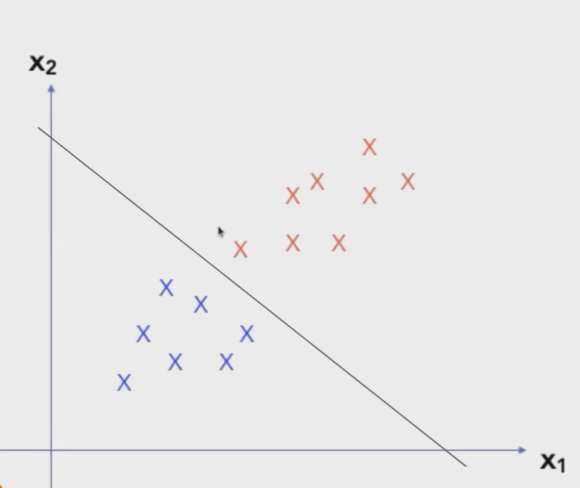
Ahora la ecuación de la recta separadora:
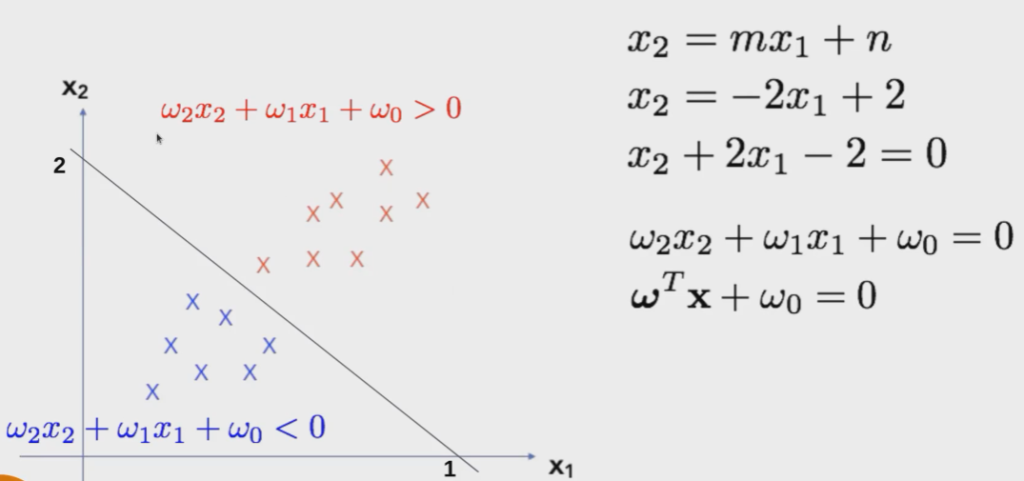
¿Cómo podemos forzar esto a que sea de máximo margen?
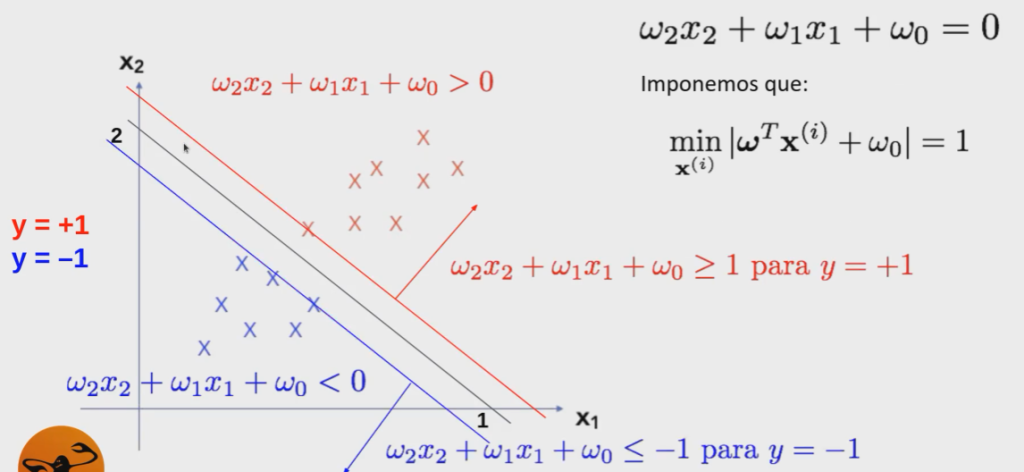
Con esto tenemos las dos fronteras. Entonces, si tenemos un plano separado, el plano con una constante también lo es:
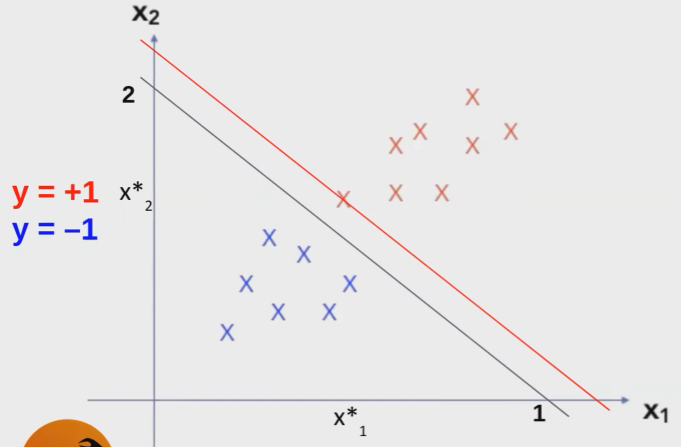
Si este es un plano separador:
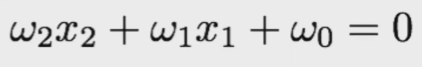
Entonces este también lo es:
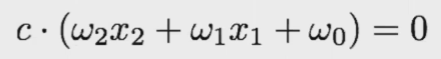
Así, escogemos C para que se cumpla la condición que nos interesa.
Ejemplo realista de SVM
Por último, veremos un ejemplo realista de SVM en problemas de clasificación. Vamos a utilizar el conjunto de datos del Pima Indian Diabetes Dataset. Recordemos que la sigla SVM significa Support Vector Machines y se traduce como máquinas de vectores soporte.
#Ejemplo realista de SVM
#cargamos datos
data = pd.read_csv ("./data/diabetes.csv", sep = ' , ', decimal = ' , ')
#preparamos los datos
features = data.columns.drop (['Outcome'])
X = data [features).values
y = data ['Outcome'].values
print ('Dimensionalidad datos: ', X.shape)Dimensionalidad datos: (768, 8)
Lo que haremos es ajustar un modelo de SVM al conjunto de datos anterior. Devolveremos las prestaciones en el conjunto de test y compararemos con la solución de Boosted Trees.
Nota: Best Test ACC (lo esperado) = 0.794
#Ejemplo realista de SVM
#paso 1
X_train, X_test, y_train, y_test = train_test_split (x, y, test_size = 0.3, shuffle = True, stratify = y, random_state = 0)
print ('Dimensionalidad train: ', X_train.shape)
print ("Dimensionalidad test: ', X_test.shape)Dimensionalidad train: (537, 8)
Dimensionalidad test: (231, 8)
#Ejemplo realista de SVM
#Paso 2
vectorC = np.logspace (-3, 3, 21)
vectorG= np.logspace (-5, 1, 21)
param_grid = {'C': vectorC, 'gamma' : vectorG)
grid = GridSearchCV (SVC (kernel = 'rbf'), scoring = 'accuracy', param_grid = param_grid, cv = 5, verbose = 2).fit (x_train, y_train)
print ("best mean cross-validation score: {: .3f}".format (grid.best_score_))
print ("best parameters: {}.format (grid.best_params_)) print (f"Log(C): (math.log10 (grid.best_params_['C'])} \nLog (gamma): {math.log10 (grid.best_params_ ['gamma'])}")
#Mostramos prestaciones en CV
scores = grid.cv_results_ ['mean_test_score'].reshape (len (vectorC), len (vectorG))
plt.figure (figsize = (10, 6))
plt.imshow (scores, interpolation = 'nearest', vmin = 0.6, vmax = 0.9)
plt.xlabel ('log (gamma)')
plt.ylabel ('log (C)')
plt.colorbar ()
plt.xticks (np.arange (len (vectorG)), np.log10 (vectorG), rotation = 90)
plt.yticks (np.arange (len (vectorC)), np.log10 (vector))
plt.title ('5 - fold accuracy')
plt.show ()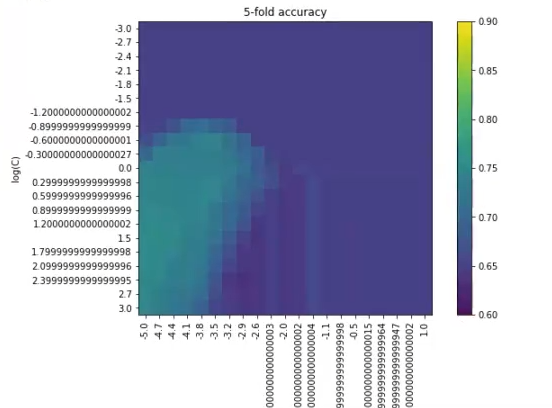
Lo primero que vemos en los resultados es que el cross – validation score ha dado 0.76, lo que quiere decir que más o menos coincide con el esperado, que era 0.79.
Nos impide ver bien qué es lo que está pasando. Es decir, este barrido no es el óptimo para este ejercicio, ya que no podemos saber cuál es el mejor valor.
Lo que haremos, por tanto, es disminuir el vmax = 0.8. El resultado será:
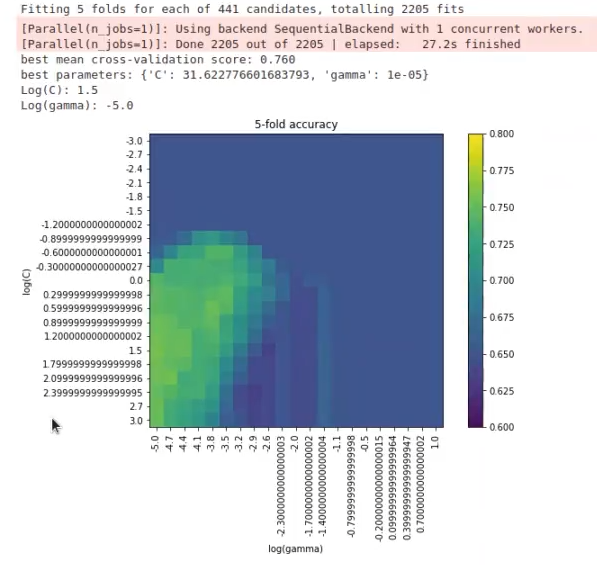
Vemos que en el sector derecho no hay nada, aparentemente, y que en el sector izquierdo es donde es probable que se encuentre el mejor accuracy. ¿Qué haríamos en este caso?
Lo que podemos hacer es modificar el vector C y el vector G, por lo que quedaría:
#Ejemplo realista de SVM
vectorC = np.logspace (-1, 6, 21)
vectorG= np.logspace (-10, 2, 21)El resultado sería:
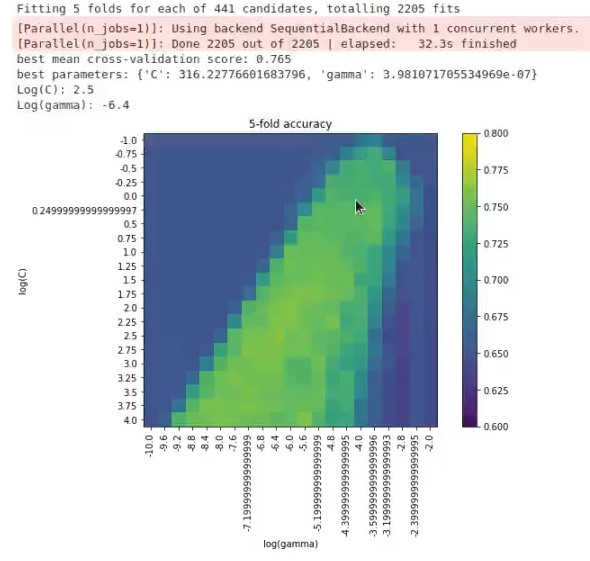
No ha quedado nada mal, ha mejorado bastante respecto al anterior.
Con esto corroboramos que el mejor accuracy se encuentra en este rango de valores. En la realidad, no nos quedaríamos con este modelo, sino que lo volveríamos mucho más complejo, aumentándole el valor de C, y seguiríamos bajando a ver qué pasa.
Si el mejor accuracy sigue dándonos en el rango inicial, es decir, si hay algún punto en el que mejora, pero solo un poco, nos quedaríamos con el modelo más simple, a no ser que veamos que las prestaciones nos están subiendo en cantidades grandes.
#Ejemplo realista de SVM
#Paso 3
Copt = grid.best_params_ ['C']
Gopt = grid.best_params_ ['gamma']
svmModel = SVC (kernel = 'rbf', gamma = Gopt, C = Copt).fit (X_train, y_train)
print ('Acc (TEST): %0.2f'% svmModel.score (X_test, y_test))Acc (TEST): 0.77
¿Qué sigue?
Ahora que hemos visto cómo funcionan las SVM, puedes dar el siguiente paso en tu proceso de aprendizaje y seguir instruyéndote con el Bootcamp Data Science, una formación intensiva en la que adquirirás todas las herramientas teóricas y prácticas para incursionar en el mercado laboral de una de las disciplinas más prolíficas de la actualidad. ¡No esperes más para impulsar tu carrera y solicita ya mismo más información!











