Un ejemplo de regresión lineal te ayudará a comprender cómo se desarrolla este tipo de cálculo que forma parte del campo del Deep Learning. Por ello, en este post, te exponemos un breve ejemplo de regresión lineal para el manejo de los macrodatos.
Ejemplo de regresión lineal
A continuación, vamos a realizar una regresión lineal sobre un determinado conjunto de datos X. Dicha regresión lineal vendrá dada por la ecuación de la recta de la forma Y^=XW+b. La solución óptima del ajuste de la recta (Wopt,bopt) sobre la distribución de datos se puede obtener minimizando la función error cuadrático medio definida como MSE=1N∑i=1N(y^i−yi)2, donde N es el número de muestras del conjunto de datos e Y es un vector con el ground truth de los mismos.
Ahora, veamos cómo ajustar una recta a un conjunto de datos que representan la inteligencia de cada uno de los personajes de Los Simpsons, desde Ralph Wiggum hasta el Doctor Frink.
# Vamos a ver cuál es la distribución de las inteligencias según las edades # normalizadas de 0 a 1, donde Maggie es la más pequeña y Montgomery Burns el # más mayor n_observations = 50 _, ax = plt.subplots(1, 1) xs = np.linspace(0., 1., n_observations) ys = 100 * np.sin(xs) + np.random.uniform(0., 50., n_observations) ax.scatter(xs, ys) plt.draw()
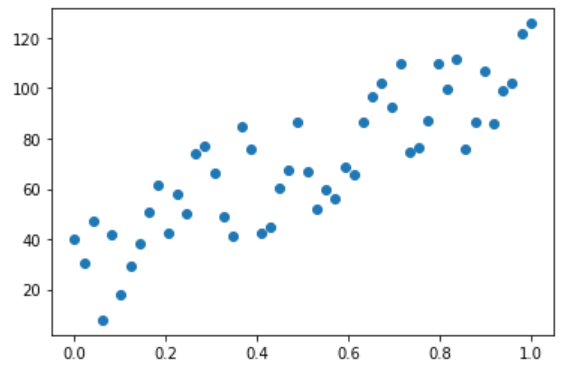
# Ahora, necesitamos dos tf.placeholders para la entrada y la salida de nuestro # algoritmo de regresión. Como ya sabéis, los placeholders son variables a las # que no es necesario asignarles un valor hasta que se ejecute el grafo X = tf.placeholder(tf.float32) Y = tf.placeholder(tf.float32) # Vamos a intentar optimizar una recta de regresión lineal: # min_(W,b) ||(X*w + b) - y||^2 # Necesitamos 2 variables, W (los pesos) y b (la bias). Los elementos de tipo # tf.Variable necesitan una inicialización, y su tipo no se puede cambiar # después. Lo que sí podemos cambiar es su valor mediante el método "assign" W = tf.Variable(tf.random_normal([1]), name='weight') b = tf.Variable(tf.random_normal([1]), name='bias') Y_pred = tf.add(tf.multiply(X, W), b) # Definimos la función de coste o pérdidas como la diferencia entre nuestras # predicciones y los valores reales loss = tf.reduce_mean(tf.pow(Y_pred - Y, 2))
# Definimos ahora el método de optimización, que va a ser el Descenso del # gradiente. Más adelante entenderemos cómo funciona. Básicamente, calcula # la variación de cada peso con respecto al error total y actualiza cada peso # de forma que disminuya el error total en las subsiguientes iteraciones. # El learning rate indica cómo de brusca es la actualización de los pesos learning_rate = 0.01 optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

# Definimos el número de iteraciones permitidas y comenzamos la inicialización
# usando la GPU
n_epochs = 1000
with tf.Session() as sess:
with tf.device("/GPU:0"):
# Con esta sentencia inicializamos todas las variables definidas
sess.run(tf.global_variables_initializer())
# Empieza el ajuste
prev_training_loss = 0.0
for epoch_i in range(n_epochs):
for (x, y) in zip(xs, ys):
sess.run(optimizer, feed_dict={X: x, Y: y})
W_, b_, training_loss = sess.run([W, b, loss], feed_dict={X: xs, Y: ys})
# Imprimimos las pérdidas cada 20 épocas
if epoch_i % 20 == 0:
print(training_loss)
# Condición de terminación
if np.abs(prev_training_loss - training_loss) < 0.000001:
print(W_, b_)
break
prev_training_loss = training_loss
# Dibujamos el resultado
plt.scatter(xs, ys)
plt.plot(xs, Y_pred.eval(feed_dict={X: xs}, session=sess))
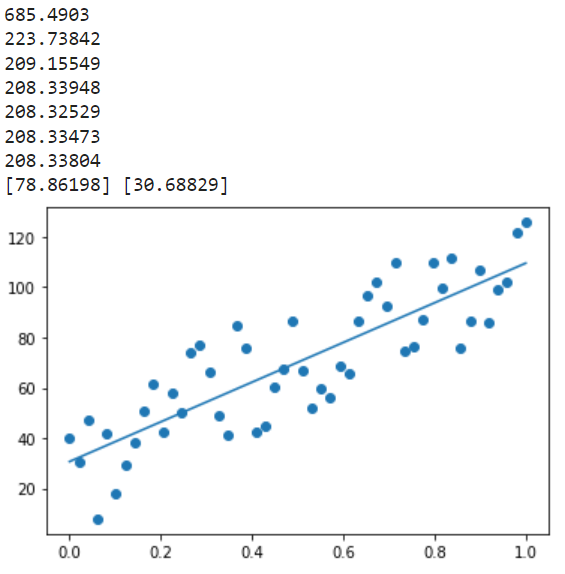
# ¿Y si quisiéramos ejecutarlo en la CPU?
n_epochs = 1000
with tf.Session() as sess:
with tf.device("/CPU:0"):
# Con esta sentencia, inicializamos todas las variables definidas
sess.run(tf.global_variables_initializer())
# Empieza el ajuste
prev_training_loss = 0.0
for epoch_i in range(n_epochs):
for (x, y) in zip(xs, ys):
sess.run(optimizer, feed_dict={X: x, Y: y})
W_, b_, training_loss = sess.run([W, b, loss], feed_dict={X: xs, Y: ys})
# Imprimimos las pérdidas cada 20 épocas
if epoch_i % 20 == 0:
print(training_loss)
# Condición de terminación
if np.abs(prev_training_loss - training_loss) < 0.000001:
print(W_, b_)
break
prev_training_loss = training_loss
# Dibujamos el resultado
plt.scatter(xs, ys)
plt.plot(xs, Y_pred.eval(feed_dict={X: xs}, session=sess))
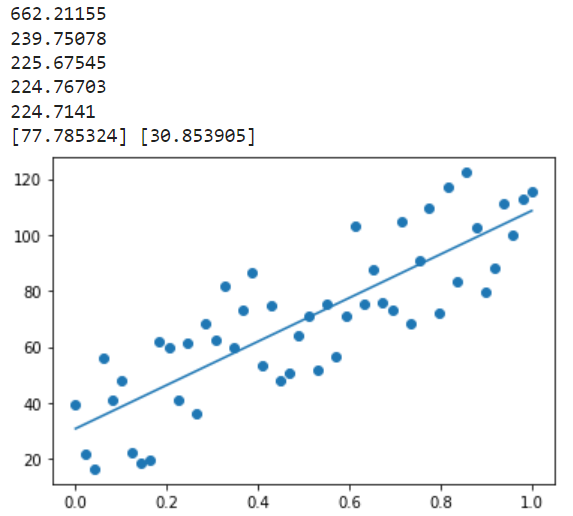
Cómo bien sabrás, con esta recta seríamos capaces de estimar la inteligencia de cualquier personaje de los Simpsons dependiendo de su edad.
Aprende más del manejo Big Data
En este post, te hemos expuesto un breve ejemplo de regresión lineal que podrás utilizar como práctica para comprender en profundidad este tema dentro del Deep Learning. Sin embargo, ¡aún queda mucho por aprender!
Por este motivo, nuestro Bootcamp Full Stack, Inteligencia Artificial & Machine Learning es perfecto para ayudarte en tu formación. En su desarrollo temático te encontrarás con las herramientas más utilizadas y más funcionales para el manejo del Big Data, con el fin de destacar el valor de la información y facilitar cuestiones como la toma de decisiones y de ruta de acción en los diferentes ámbitos. En menos de nueve meses, podrás contar con los aprendizajes necesarios para desenvolverte como un experto en el procesamiento de los macrodatos. ¡Apúntate ahora!











