Cuando empecé a trabajar con modelos predictivos y sistemas de análisis de datos complejos, descubrí que la estadística bayesiana ofrecía una ventaja clave sobre los métodos tradicionales: me permitía incorporar conocimiento previo en mis análisis y actualizar mis hipótesis a medida que llegaban nuevos datos. Este enfoque es esencial para tomar decisiones más acertadas en entornos de incertidumbre, como los que enfrentamos constantemente en Big Data, medicina, economía o inteligencia artificial.
Si estás buscando entender qué es la estadística bayesiana y cómo se aplica en la práctica, aquí te explico todo lo que necesitas saber desde la experiencia de quien la ha utilizado en proyectos reales.
¿Qué es la estadística bayesiana?
La estadística bayesiana es un enfoque que interpreta la probabilidad como una medida de creencia o certeza, en lugar de limitarla a la frecuencia de ocurrencia de un evento. Lo que la hace diferente es que permite combinar datos con conocimiento previo, y actualizar esa información a medida que se obtiene nueva evidencia.
En el corazón de esta metodología está el teorema de Bayes, que proporciona una fórmula para calcular la probabilidad de una hipótesis dada cierta evidencia:
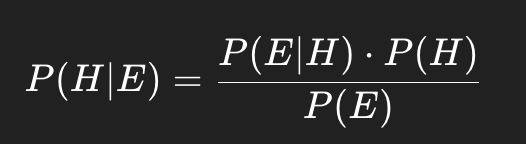
- P(H∣E): probabilidad posterior (hipótesis tras observar la evidencia)
- P(E∣H): verosimilitud (probabilidad de observar la evidencia si la hipótesis es cierta)
- P(H): probabilidad a priori (creencia inicial sobre la hipótesis)
- P(E): probabilidad total de la evidencia
Gracias a esta fórmula, podemos ajustar nuestras creencias de forma matemática cada vez que obtenemos nuevos datos.
¿Qué hace única a la estadística bayesiana?
Desde mi experiencia, estas son las razones por las que la estadística bayesiana marca la diferencia:
- Integra información previa: no partes de cero, sino que puedes incorporar conocimiento experto o histórico.
- Se actualiza con nueva evidencia: cada dato nuevo afina tus predicciones.
- Más intuitiva en muchos casos: especialmente cuando hablamos de probabilidades condicionales o decisiones bajo incertidumbre.
- Útil incluso con pocos datos: algo que agradeces mucho cuando los recursos son limitados.

Aplicaciones prácticas de la estadística bayesiana
He usado modelos bayesianos en diferentes sectores, y sus aplicaciones son tan amplias como útiles:
- Medicina: para actualizar diagnósticos con nuevos resultados clínicos.
- Marketing y negocio: para afinar segmentaciones y predicciones de comportamiento del cliente.
- Machine Learning: en algoritmos probabilísticos y redes bayesianas.
- Finanzas: para evaluar el riesgo de inversiones condicionadas a distintos escenarios económicos.
- Big Data: donde se combina con técnicas de inferencia y análisis en tiempo real.
Por ejemplo, si estás analizando la probabilidad de churn (abandono de clientes), un enfoque bayesiano te permite ajustar esa probabilidad cada vez que el cliente realiza una acción nueva (abrir un correo, cancelar una suscripción, etc.).
¿Por qué deberías aprender estadística bayesiana?
Porque vivimos en un mundo lleno de incertidumbre y datos incompletos. La estadística bayesiana no solo acepta esa realidad, la abraza. Es especialmente potente cuando necesitas combinar la intuición de un experto con los datos disponibles para tomar decisiones mejor fundamentadas.
Además, muchos modelos modernos en ciencia de datos y aprendizaje automático se apoyan en fundamentos bayesianos, desde los clasificadores Naive Bayes hasta los modelos jerárquicos más complejos.
Conclusión sobre la estadística bayesiana
La estadística bayesiana es mucho más que una técnica matemática: es una forma de pensar y razonar con datos. Su capacidad de actualizar creencias y trabajar con incertidumbre la hace imprescindible para cualquier persona que quiera entender realmente lo que los datos están diciendo, especialmente en contextos de alta complejidad.
¿Quieres dominar esta y muchas otras técnicas de análisis avanzado? Entonces el Curso de Big Data y Data Science es para ti. Aprenderás a trabajar con datos reales, construir modelos predictivos robustos y aplicar estadística en escenarios empresariales y tecnológicos de alto nivel. Si te apasiona la analítica y quieres transformar tu carrera, este es el paso que necesitas.











