La estimación de funciones polinómicas en estadística es fundamental cuando dentro de tu población de datos estos poseen expresiones de polinomio. Este es un conocimiento muy específico y especializado que resulta necesario cuando trabajas con un gran volumen de datos.
Por ello, en el desarrollo de este post, te explicamos todo lo que necesitas saber sobre la estimación de funciones polinómicas en estadística Big Data.
Estimación de funciones polinómicas en estadística
Podrás desarrollar una estimación de funciones polinómicas en estadística del tipo:
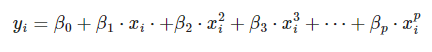
Simplemente, reescribiéndolo como un modelo lineal múltiple: [ \begin{bmatrix} y_1 \ y_2 \ \vdots \ y_n, así:
\end{bmatrix}
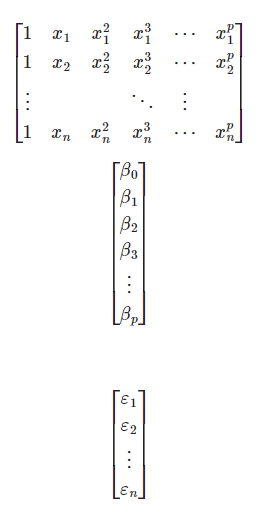
/] Lo que se puede simplificar como:
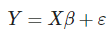
Su desarrollo para la estimación de funciones polinómicas en estadística sería:
n<-100
x<-seq(-10,10,length.out = n)
x0<-rep(1,n)
x1<-x
x2<-x^2
x3<-x^3
X<-matrix(c(x0,x1,x2,x3),nrow=n,byrow = F)
beta<-matrix(c(1,1,3,0.5),nrow=4)
Y<-X %*% beta+rnorm(n,sd = 50)
plot(X[,2],Y,pch='*')
est_beta<-solve(t(X) %*% X) %*% t(X) %*% Y
est_Y<-X %*% beta
lines(X[,2],est_Y,col="blue")
print("El valor estimado de beta es:")
est_beta
print("El valor real de beta es:")
beta
[1] «El valor real de beta es:»
A matrix: 4 × 1 of type dbl
| 6.8753944 |
| -0.9760129 |
| 2.9935223 |
| 0.5393072 |
A matrix: 4 × 1 of type dbl
| 1.0 |
| 1.0 |
| 3.0 |
| 0.5 |
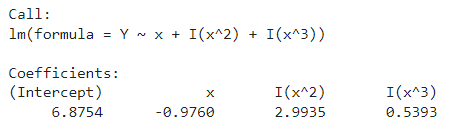
modelPoly3<-lm(Y~x+I(x^2)+I(x^3)) #modelPoly3<-lm(Y~poly(x,3)) modelPoly3
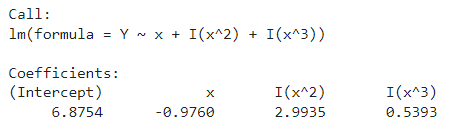
summary(modelPoly3)

Sobreajuste
Por otra parte, para la estimación de funciones polinómicas en estadística, debes tener en cuenta el sobreajuste (overfitting) que ocurre en los modelos que tienen un grado polinómico tan alto que empiezan a seguir al ruido. Se sobreajustan demasiado a los datos, perdiendo una visión más general de los datos y proporcionando predicciones peores.
En este caso, en lugar de estar aprendiendo la relación básica entre dos variables, estarías aprendiendo los errores. El modelo intenta integrar los errores para dar una respuesta más exacta. El problema es que, al coger otra vez variables similares, los errores cambian, por lo que lo aprendido con los errores anteriores ya no sirve. Es decir, nuestro modelo sería erróneo.
La esencia del modelo se basa en encontrar una predicción que funcione para la mayoría de los casos, no para los datos que estamos viendo ahora mismo, sino también para los datos futuros.
modelOverfit <- lm(Y~poly(x,27)) summary(modelOverfit)
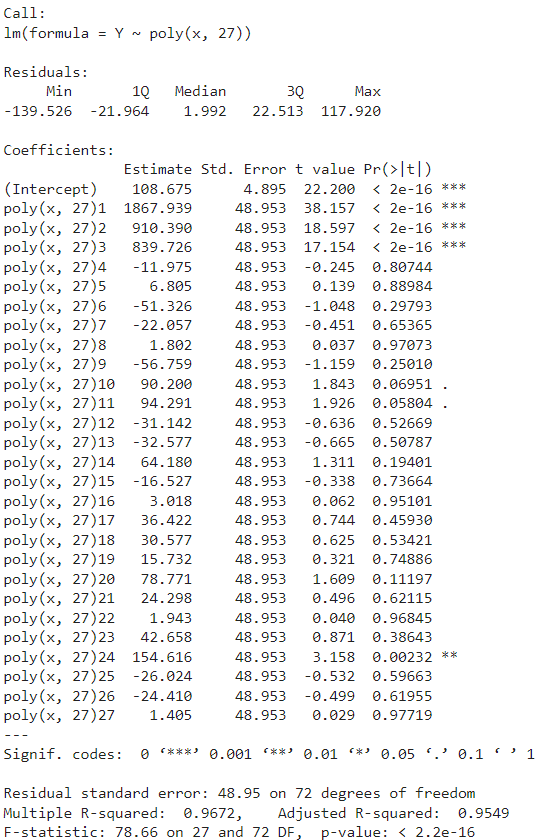
plot(X[,2],Y,pch='*') xp<-seq(-10,10,by=0.1) yp<-predict(modelOverfit,data.frame(x=xp)) lines(xp,yp,col="blue") lines(xp,predict(modelPoly3,data.frame(x=xp)),col="red")
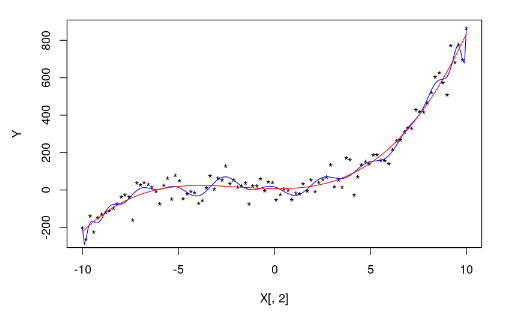
paste("Polinomio grado 27: Rsquared:",summary(modelOverfit)$r.squared)
paste("Polinomio grado 27: Residual standard error",sqrt(sum(summary(modelOverfit)$residuals^2)/(length(summary(modelOverfit)$residuals)-25)))
paste("Polinomio grado 3: Rsquared:",summary(modelPoly3)$r.squared)
paste("Polinomio grado 3: Residual standard error",sqrt(sum(summary(modelPoly3)$residuals^2)/(length(summary(modelPoly3)$residuals)-4)))
‘Polinomio grado 27: Rsquared: 0.967209419375986’
‘Polinomio grado 27: Residual standard error 47.9644017918624’
‘Polinomio grado 3: Rsquared: 0.954608949821556’
‘Polinomio grado 3: Residual standard error 49.8797892133702’
¿Cómo encontrar el mejor modelo?
Para una óptima estimación de funciones polinómicas en estadística, debes tener el mejor modelo. Para ello, usa el p-valor de los coeficientes o busca entre todos los modelos el de menor AIC (Criterio de Información de Akaike), que es un estimador de la calidad relativa del modelo que tiene en cuenta su complejidad.
A medida que se aumenta el número de parámetros de entrada o de grados de un polinomio, el valor del error cuadrático medio va a ser mejor, porque el error cuadrático medio disminuye. El AIC penaliza los modelos complejos en favor del los sencillos para evitar el sobreajuste.
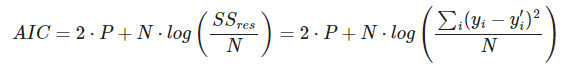
Donde P es el número de variables que se utilizan en el modelo y N el número de muestras. Cuanto menor sea el valor del AIC, mejor será el modelo.
paste("Polinomio grado 27, AIC:",AIC(modelOverfit))
paste("Polinomio grado 3, AIC:",AIC(modelPoly3))
‘Polinomio grado 27, AIC: 1087.11132068148’
‘Polinomio grado 3, AIC: 1071.62868617455’
En R existe la función stepAIC que nos encuentra el AIC mínimo tras probar con diferentes combinaciones.
library(MASS) datadf<-data.frame(y=Y,x=x) model<-lm(formula=y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5)+I(x^6)+I(x^7)+I(x^8),datadf) summary(model)
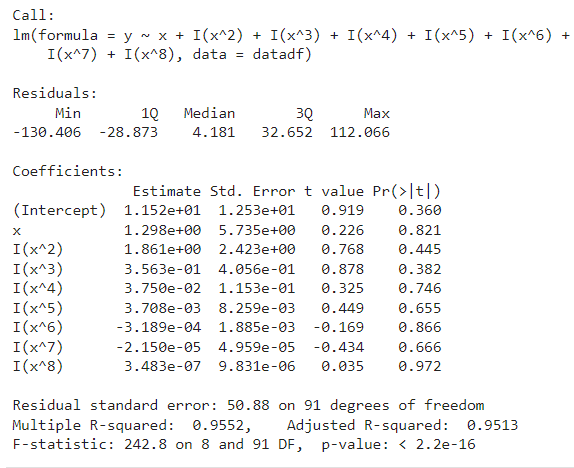
stepAIC(model,trace=FALSE)
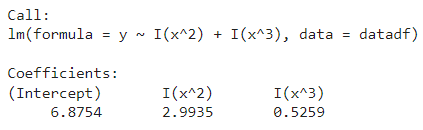
modelOptim<- lm(formula = y ~ I(x^2) + I(x^3), data = datadf)
modelOptim
plot(X[,2],Y,pch='*')
xp<-seq(-10,10,by=0.1)
yp<-predict(modelOptim,data.frame(x=xp))
lines(xp,yp,col="blue")
modelPoly3<-lm(Y~x+I(x^2)+I(x^3))
lines(xp,predict(modelPoly3,data.frame(x=xp)),col="red")
legend(-10,800,c("polinomio menor AIC","polinomio grado 3"),pch='-',col=c('blue','red'),y.intersp=2)
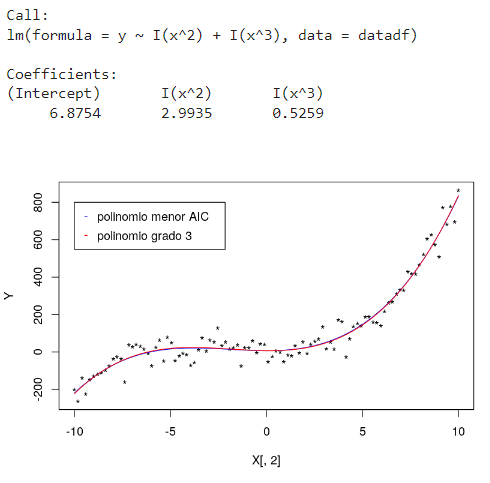
summary(modelOptim) summary(modelPoly3)

Aunque el error sea menor con el polinomio de grado 24, es mejor utilizar el modelo con un el polinomio de grado 3, porque el modelo de grado 24 está aprendiendo sobre el ruido.
¿Quieres aprender más sobre el Big Data?
En este post, te hemos explicado qué es la estimación de funciones polinómicas en estadística para el manejo del Big Data. Sin embargo, ¡aún queda mucho más por aprender al respecto! Por ello, te presentamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning.
Por medio del mismo, podrás aprender más sobre las demás herramientas Big Data a través de diferentes módulos, como el de Big Data Architecture. Allí, verás una imagen completa del proceso de carga, clasificación, resguardo, gestión y presentación de los datos a través de diferentes lenguajes, herramientas y sistemas. Además, podrás instruirte tanto de manera teórica como práctica. ¡No esperes más y apúntate ya!











