A continuación veremos los métodos de filtrado para clasificación no linealmente separable que existen en machine learning.
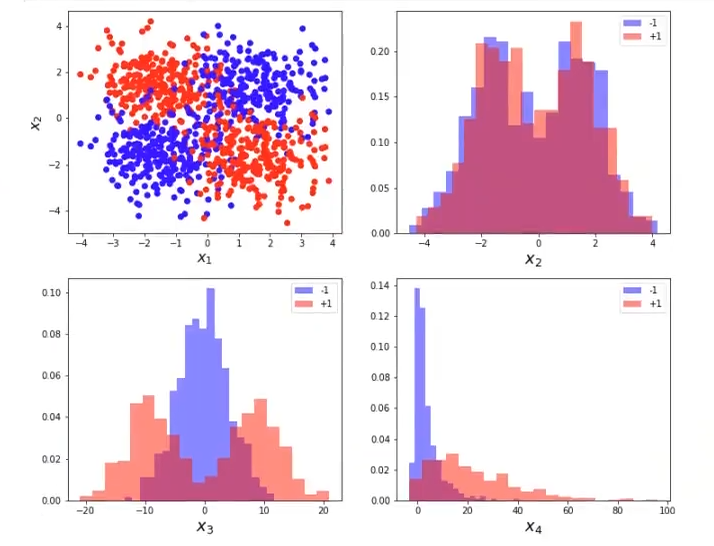
Vamos a analizar el problema XOR, definido por las variables x1 y x2. Añadimos, además, dos variables relevantes x3 y x4, con capacidad discriminatoria y que, por tanto, pueden ayudar a mejorar las prestaciones del problema de clasificación bajo estudio. Por último, se incluyen 20 variables ruidosas irrelevantes.
Filtrado para clasificación no linealmente separable: ejercicio
Así pues, tenemos que x1, x2, x3 y x4 son importantes y que hay otras variables (E = 2 * np.random.randn (N, 20)) que son puro ruido:
#filtrado para clasificación no linealmente separable
np.random.seed (0)
# -- parameters
N = -1000
mu = 1.5 #Cambia este valor
sigma = 1 #Cambia este valor
#variables auxiliares.
unos = np.ones (int (N / 4))
random4 = sigma * np.random.randn (int (N / 4), 1)
random2 = sigma * np.random.randn (int (N / 2), 1)
#features
y = np.concatenate ([-1 * unos, unos, unos, -1 * unos])
X1 = np.concatenate ([-mu + random4, mu + random4, -mu + random4, mu + random4])
X2 = np.concatenate ([+mu + random2, -mu + random2])
X3 = 3 * (x1 + x2) + np.sqrt (2) * np.random, randn (N,1)
X4 = 2 * np.square ((X1 + X2)) + np.sqrt (2) * np.random.randn (N, 1)
E = 2 * np.random.randn (N, 20) #noisy variables
X = np.hstack ((X1, X2, X3, X4, E))
plt.figure (figsize = (12, 10))
plt.subplot (2, 2, 1)
plt.scatter (x1, x2, c = y.reshape (-1, 1), cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)
#filtrado para clasificación no linealmente separable
for i in range (3):
plt.subplot (2, 2, i + 2)
plt.hist (X [y < 0, i + 1], bins = 20, normed = True, alpha = 0.5, label = '-1', color = 'b')
plt.hist (X [y > 0, i + 1], bins = 20, normed = True, alpha = 0.5, label = '+1', color = 'r')
plt.legend (loc = 'upper right')
plt.xlabel ("$x_{ }$".format (i + 2), fontsize = 18)
plt.show ()Pintamos el problema de XOR
Ahora lo que haremos es aplicar el f classif y el mutual info classif al problema en general:
#filtrado para clasificación no linealmente separable
#son 24 variables porque hay 4 declaradas arriba (X1, X2, X3, X4) y 20 variables aleatorias que son ruido: en total 24.
featureNames = ['x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x9', 'x10', 'x11', 'x12', 'x13', 'x14', 'x15', 'x16', 'x17', 'x18', 'x19', 'x20', 'x21', 'x22', 'x23', 'x24']
#do calculations
f test, = f_classif (x, y)
f_test /= np.max (f_test)
mi = mutual_info_classif (x, y)
mi /= np.max (mi)
#do some plotting
plt.figure (figsize = (20, 5))
plt.subplot (1, 2, 1)
plt.bar (range (X.shape [1]), f_test, align = "center")
plt.xticks (range (X.shape [1]), featureNames, rotation = 45)
plt.xlabel ('features')
plt.ylabel ('Ranking')
plt.title ('$F Test$ score')
#filtrado para clasificación no linealmente separable
plt.subplot (1, 2, 2)
plt.bar (range (X.shape [1]), mi, align="center")
plt.xticks (range (X.shape [1]), featureNames, rotation = 45)
plt.xlabel ('features')
plt.ylabel ('Ranking')
plt.title ('Mutual information score')
plt.show ()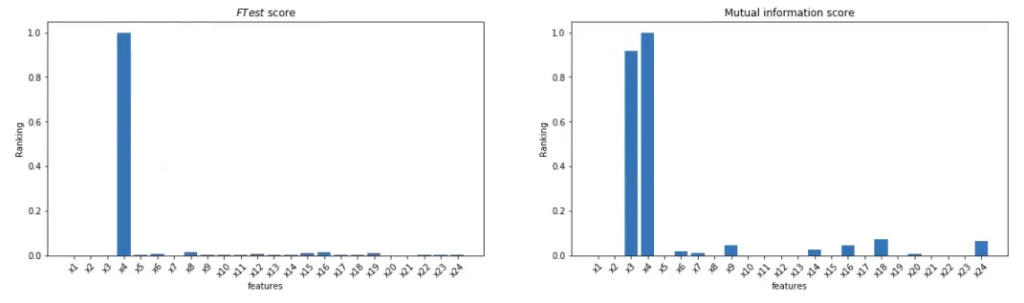
Por un lado, F Test nos dice que la única variable importante es x4. Por otro lado, mutual info nos dice que tanto x3 como x4 son importantes, que algunas de las variables de ruido tienen cierta relevancia y que x1 y x2 no importan; no obstante, nosotros sabemos que el problema de XOR se puede definir con las variables x1 y x2.
¿Qué pasa, entonces? Recordemos que el problema XOR se resuelve, si nos fijamos en la clasificación de x1 en la primera imagen, observando que todo lo azul es donde x1 y x2 son positivas a la vez o que, por el contrario, x1 y x2 son negativas a la vez. Todo lo rojo, en el otro lado del espectro, es donde x1 es positiva y x2 es negativa o viceversa.
Es decir, el problema de XOR es un problema totalmente soluble, completamente separable, pero necesitamos una interacción entre las variables x1 y x2 para poder resolverlo. Es decir, necesitamos conocer x1 y x2 al mismo tiempo para poder darle solución al problema.
Entonces, como estos métodos de filtrado para clasificación no linealmente separable no detectan las interacciones entre variables y lo único que hacen es juntar x1 o x2 con variable objetivo, no van a detectar esa relevancia y, por tanto, no son viables para este tipo de ejercicios donde se tienen que resolver problemas de XOR.
Ahora que hemos visto cómo funcionan los métodos de filtrado para clasificación no linealmente separable, podemos escalar el siguiente nivel y seguir aprendiendo más sobre una de las disciplinas de la actualidad mejor pagadas y más demandadas. Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que podrás aprender todo lo necesario para incursionar en este mundillo. ¡Anímate a transformar tu futuro y solicita más información!











