En este post te explicaremos cómo funciona la fórmula matemática del descenso de gradiente.
Recordemos que el descenso de gradiente es un método de optimización iterativo, esto quiere decir que cada iteración que ejecutemos nos acercará un poco más al mínimo de la función, es decir, a la solución.
El descenso de gradiente
En el concepto de descenso de gradiente debemos tener en cuenta la palabra descenso, que implica descender. En el ejercicio sobre el arg min en un gradiente descendente, proponíamos ver el descenso de gradiente como el descenso de una montaña. Lo que queremos es reducir la distancia entre nosotros y la superficie de la montaña, es decir, bajar tan rápido como nos sea posible. Esto es el descenso de gradiente.
Pero no existe solo existe el descenso; si hay un descenso, su inversa también tiene que existir. Tenemos, pues, dos posibilidades:
- El descenso de gradiente.
- El ascenso de gradiente.
Fórmula matemática del descenso de gradiente
¿Cómo se resume esto matemáticamente? ¿Cuál es la fórmula matemática del descenso de gradiente? Podríamos decir que Xt es igual a Xt – 1 por un parámetro y por la derivada parcial de la función de x:
Xt = Xt-1 * 2∇ f (x)
Desglosemos un poco esta fórmula matemática del descenso de gradiente. Siguiendo el ejemplo de la montaña, ahora estamos arriba, en el step 1. Cuando estamos en el step 1, queremos calcular la posición en la que vamos a acabar dentro de la montaña al descender; este es el lugar donde comenzaremos el step 2.
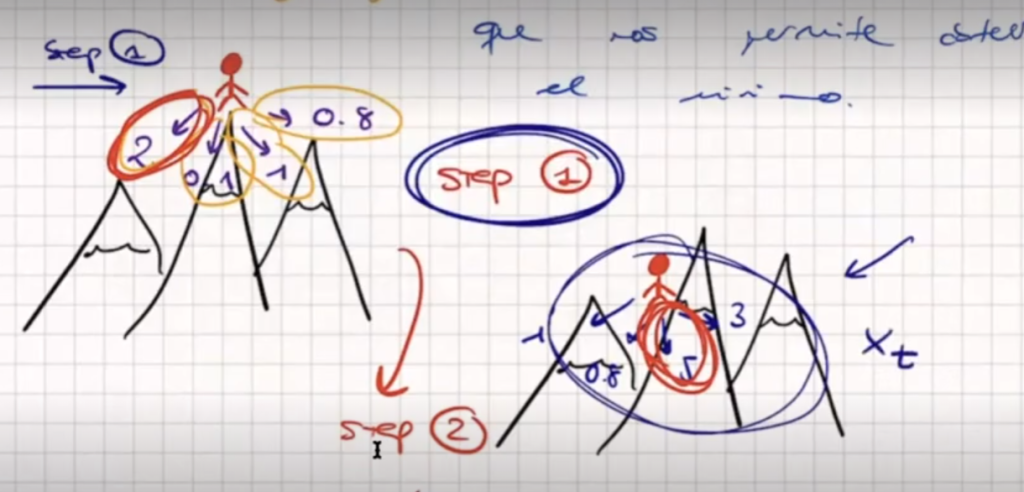
En este caso, queremos saber dónde vamos a acabar, es decir, estamos calculando Xt. ¿Qué usamos para calcular Xt (x de t)? Pues usamos el valor actual, el que ya conocemos. En nuestro ejemplo, el valor actual es la posición en el pico de la montaña, lo que matemáticamente se traduciría como Xt-1 en la fórmula matemática del descenso de gradiente.
Para calcular Xt tenemos que usar el valor Xt-1. Esto sucede porque, claramente, necesitamos saber dónde estamos para saber hacia dónde vamos a ir. En caso contrario, no sabemos el resultado hacia el que nos va a llevar.
Entonces, eso es lo que significa la primera parte de la ecuación Xt = Xt-1. Xt es el siguiente paso que vamos a dar en el descenso por la montaña. Xt-1 es el punto de partida.
No obstante, ocurren cosas muy distintas con la segunda parte de la fórmula matemática del descenso de gradiente, es decir, el 2∇ f (x). Vemos que a esto lo antecede un menos; este menos viene porque estamos descendiendo y el 2 que vemos es el learning rate.
∇ f (x) en la fórmula matemática del descenso de gradiente no es más que el gradiente de la función f (x) (f de x).
Objetivo del descenso de gradiente
Para comprender la fórmula matemática del descenso de gradiente, veamos a fondo cómo funciona este. Tenemos una curva en la recta, en este caso es una función f (x). Empezamos en un punto y, como hemos dicho, queremos llegar al mínimo; por tanto, calcularemos la dirección hacia la que el descenso es más rápido. Veamos:
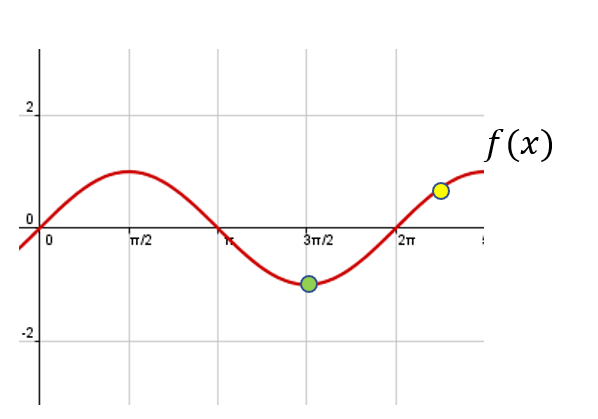
¿Cómo descenderíamos más rápido, si seguimos el camino marcado hacia la derecha o hacia la izquierda de la bolita amarilla? Por lógica, diríamos que debemos seguir hacia la izquierda, y en eso tendríamos razón, es mucho más rápido si lo hacemos por el lado izquierdo. Veamos qué pasa si vamos hacia la izquierda.

El punto amarillo en la parte inferior corresponde a Xt; por otro lado, el punto amarillo en la parte superior corresponde a Xt-1. Para calcular el segundo punto, hemos tenido que usar el primero, como se indica más arriba.
¿Quieres seguir aprendiendo?
El Big Data es una de las áreas en las que más trabajos se ofertan. Para poder acceder a este tipo de opciones laborales, que son de las mejor pagadas en el mercado actual, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación intensiva podrás aprender de forma teórica y práctica para obtener el trabajo de tus sueños en pocos meses. ¡No esperes más para impulsar tu carrera profesional y solicita información ahora mismo!











