Cuando comencé a trabajar con modelos estadísticos más complejos, me di cuenta de que comprender la función de densidad condicional era esencial para analizar cómo una variable aleatoria se comporta bajo ciertas condiciones. Esta herramienta permite calcular la probabilidad de un evento dado que otro ha ocurrido, lo cual es fundamental en campos como la estadística bayesiana, el aprendizaje automático y la inferencia estadística.
¿Qué es la función de densidad condicional?
La función de densidad condicional describe la probabilidad de que una variable aleatoria continua tome un valor específico, dado que otra variable ha tomado un valor determinado. Matemáticamente, si XXX y YYY son variables aleatorias continuas con una función de densidad conjunta ffX,Y(x,y), la función de densidad condicional de YYY dado X=xX = xX=x se define como:
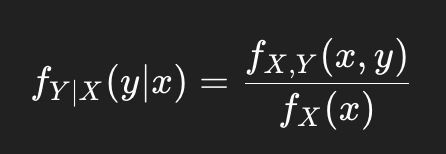
donde fx(x) es la función de densidad marginal de X. Esta fórmula nos permite actualizar nuestras creencias sobre Y cuando conocemos el valor de X.
Propiedades clave
La función de densidad condicional comparte varias propiedades con las funciones de densidad estándar:
- No negatividad:
para todos los valores de y.
- Normalización: La integral de
sobre todos los valores de y es igual a 1, es decir
- Cálculo de probabilidades: La probabilidad de que Y esté en un intervalo dado [a,b], dado X=x, se calcula como P (a ≤ Y ≤ b | X=x) = ∫ab fY∣X(y∣x)dy
Estas propiedades aseguran que la función de densidad condicional sea una herramienta válida para modelar la incertidumbre bajo condiciones específicas.

Ejemplo práctico
Supongamos que estamos analizando el tiempo que tarda un servidor en responder a una solicitud, y sabemos que este tiempo depende de la carga actual del sistema. Si representamos el tiempo de respuesta como YYY y la carga del sistema como XXX, la función de densidad condicional fY∣X(y∣x)f_{Y|X}(y|x)fY∣X(y∣x) nos permite modelar cómo varía el tiempo de respuesta en función de la carga. Por ejemplo, podríamos encontrar que, dado que la carga del sistema es alta (X=xX = xX=x), la probabilidad de que el tiempo de respuesta sea mayor también aumenta.
Este tipo de análisis es crucial para optimizar el rendimiento de sistemas y garantizar niveles de servicio adecuados.
Aplicaciones en el mundo real
La función de densidad condicional tiene múltiples aplicaciones en diversas áreas:
- Estadística bayesiana: Para actualizar probabilidades a medida que se obtiene nueva información.
- Aprendizaje automático: En modelos como las redes bayesianas, donde se modelan dependencias condicionales entre variables.
- Econometría: Para modelar relaciones entre variables económicas bajo ciertas condiciones.
- Ingeniería: En análisis de confiabilidad y evaluación de riesgos condicionados a ciertos eventos.
Comprender y aplicar correctamente la función de densidad condicional permite construir modelos más precisos y tomar decisiones informadas basadas en datos.
Conclusión
La función de densidad condicional es una herramienta poderosa que permite analizar cómo una variable aleatoria se comporta bajo condiciones específicas. Su comprensión es esencial para profesionales que trabajan con datos y modelos estadísticos complejos.
Si deseas profundizar en este y otros conceptos avanzados de estadística y su aplicación en entornos reales, te invitamos a explorar nuestro Curso Big Data y Data Science. Aprenderás a manejar grandes volúmenes de datos, implementar soluciones en la nube y aplicar técnicas estadísticas avanzadas para optimizar procesos y tomar decisiones basadas en datos. ¡Inscríbete ahora y lleva tu carrera al siguiente nivel!



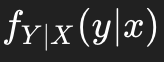 sobre todos los valores de y es igual a 1, es decir
sobre todos los valores de y es igual a 1, es decir 







