La función de enlace probit su usa, generalmente, para parámetros que se encuentran en un intervalo unitario. Esta es la función de distribución acumulada de una distribución normal estándar.
¿Cómo se ejecuta la función de enlace Probit?
En vez de usar la función logit:
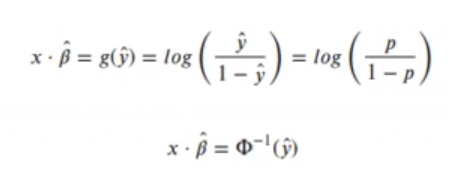
Se puede usar la función de enlace probit:
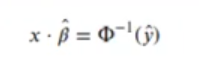
Esta es mucho más reducida y, en ella, θ-1 (y) es la inversa de la función acumulativa de probabilidad de una función normal de media 0 y varianza 1: N (0, 1).
De esta forma, se podría considerar que la probabilidad de y sigue una función normal en la función de enlace probit:
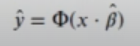
Así, la probabilidad de que y = 1 es:
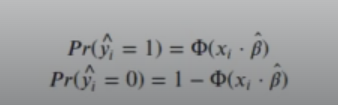
options (repr.plot.height = 4, repr.plot.width = 6)
y <- seq (-10, 10, length.out = 100)
x_logit <- 1 / (1 + exp (-y))
plot (y, x_logit, t = "l", col = 'red', ylab = 'X')
x_probit <- pnorm (y)
lines (y, x_probit, t = "l", col = 'blue')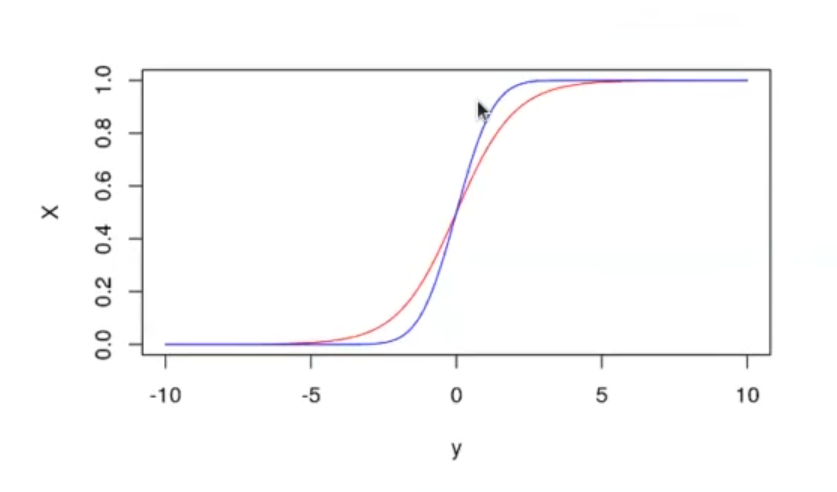
plot (x_logit, y, t = "l", col = 'red', ylab = 'X')
lines (x_probit, y, t = "l", col = 'blue')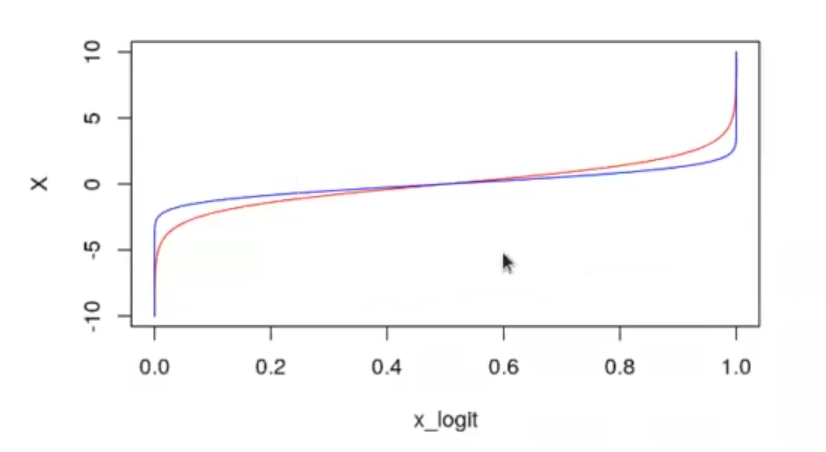
set.seed (123)
x <- rep (c (rep (0.2, 3), rep (0.4, 2), rep (0.1, 6)), 10)
y <- sapply (x, function (xi) rbinom (1, size = 1, prob = xi * 2 + 0,1))
df <- data.frame (y, x)
head (df)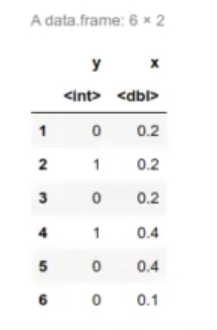
model_probit <- glm (data = df, formula = y ~ x, family = binomial ('probit'))
summary (model_probit)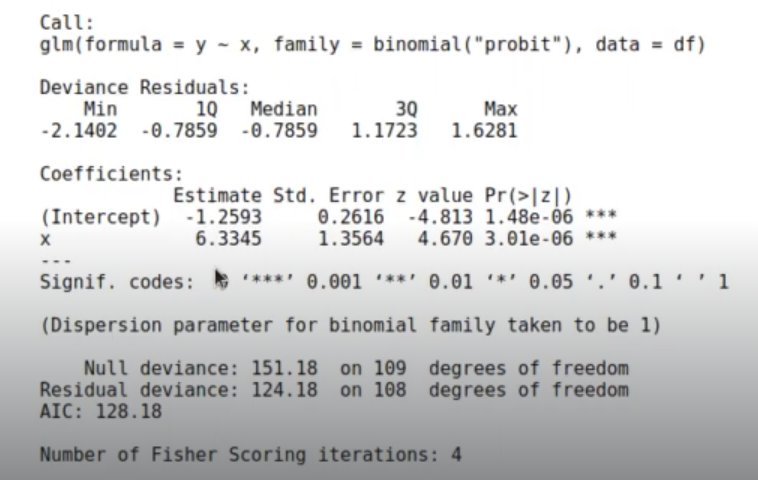
model logit <- glm (data = df, formula = y ~ x, family = binomial ('logit'))
summary (model_logit)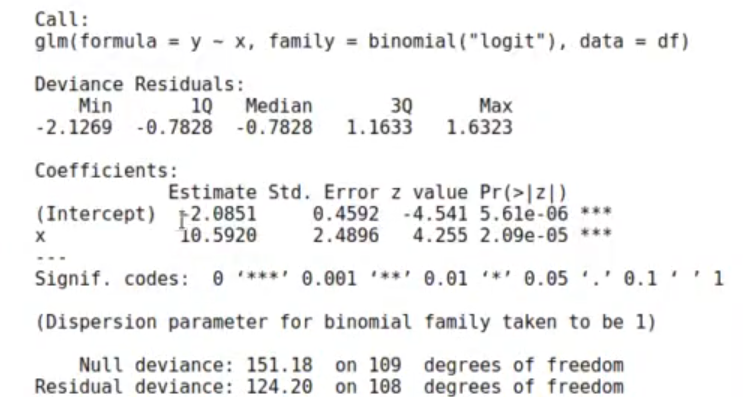

x_lin <- seq (0, 0.4, length.out = 20)
y_est_logit <- model_logit$_coefficient [1] + model_logit$_coefficient [2] * x_lin # log (odds)
y_est_probit <- model_probit$_coefficient [1] + model_probit$_coefficient [2] * x_lin
y_real <- x_lin * 2 + 0.1 # probability
log_odds_real <- log (y_real / (1 - y_real)) #logit
plot (x_lin, log_odds_real, t = 'l', col = 'red', ylab = 'y transformada')
lines (x_lin, y_est_logit, col = "red", lty=2)
probit = qnorm (y_real)
lines (x_lin, probit, t = 'l', col = 'blue')
lines (x_lin, y_est_probit, col = "blue", lty = 2)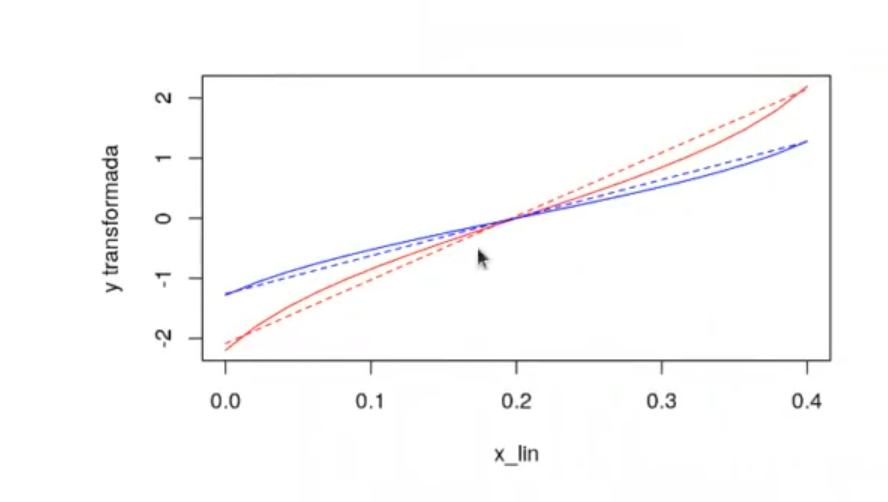
x_lin <- seq (0, 0.4, length.out = 20)
y_est_logit <- predict (model_logit, data.frame (x = x_lin), type = "response")
y_est_probit <- predict (model_probit, data.frame (x = x_lin), type = "response")
y_real <- x_lin * 2 + 0.1 # probability
plot (x_lin, y_real, t = 'l', col = 'gray')
lines (x_lin, y_est_logit, t = '1', col = 'blue')
lines (x_lin, y_est_probit, col = "red")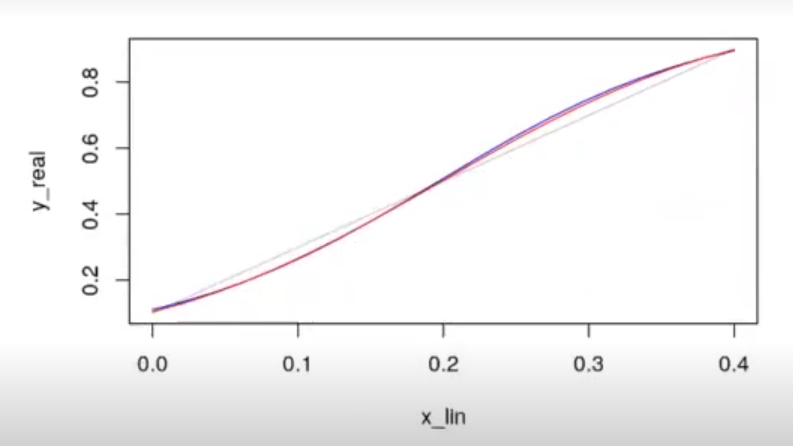
Los coeficientes de una regresión logística utilizando una función de enlace logit eran fáciles de interpretar y tenían un modelo de respuesta simple, teniendo en cuenta que la regresión lineal daba simplemente el logaritmo de la razón de momios.
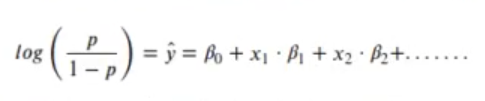
Cada coeficiente (elevado a e) simplemente aumenta de forma multiplicativa la razón de momios:
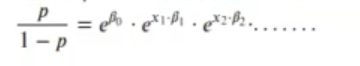
Pero en la regresión logística utilizando la función de enlace probit como función de enlace esto es más complicado, ya que los coeficientes cambian:
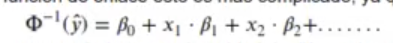
Podrían interpretarse como la diferencia en el z-score asociado con cada unidad de diferencia en la predicción de la variable.
La función de enlace probit es práctica, pero hay muchas otras alternativas que puedes usar en el análisis y procesamiento de tus datos, como logit, Poisson, etc.
Por eso, si quieres seguir aprendiendo sobre estas otras funciones y propiedades avanzadas del Big Data y el data mining, te invitamos a que realices nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, en donde podrás encontrar a los mejores profesionales. Estos te guiarán en tu proceso de aprendizaje para incursionar en el mundo laboral y conseguir excelentes oportunidades de empleo con una avanzada formación en tan solo 8 meses. ¡Solicita más información e inscríbete ya!







