La relación entre la función de pérdida vs función de activación es algo que debe ser analizado cuando te reconoces como un data scientist, puesto que esta potencia el procesamiento y los resultados del análisis Big Data. Por ello, en este post, te explicamos cómo funciona la función de pérdida vs función de activación.
Función de pérdida vs función de activación
En primer lugar, hay que partir de que la función de pérdida vs función de activación es una relación indiscutible e indispensables en el estudio y análisis de redes neuronales profundas, puesto que estas se encuentran estrechamente ligadas. Sin embargo, primero te aclararemos qué es cada una de ellas:

- La función de pérdida es la función que nos indica cuánto nos hemos equivocado con nuestras predicciones, es decir, cuánto hemos perdido dentro del procesamiento de data en Deep Learning.
- La función de activación parte de los casos en los que nos encontramos frente a problemas de data que son imposibles de solucionar con combinaciones lineales. Por tanto, se necesita de una forma de introducir no linealidades y de eso es de lo que se encarga la función de activación.
De manera que la relación de la función de pérdida vs función de activación se plantea a partir de que, si bien puedes no rectificar la función de activación con la función de pérdida antes de seguir con el procesamiento (aunque es lo más recomendable), igual tendrás que confrontar la función de pérdida con la función de activación cuando se hable de las no linealidades en los macrodatos.
Ejemplo: función de pérdida vs función de activación
# definimos la función para entrenar nuestra red con los parámetros deseados def train_network_decay_fnact_b1_mse(activation_function, learning_rate, lr_decay, batch_size, n_epochs): # creamos los contenedores para nuestras entradas y salidas x = tf.placeholder(tf.float32, [None, 784]) # imágenes del mnist: 28*28=784 y = tf.placeholder(tf.float32, [None, 10]) # número indicando la clase 0-9 => 10 clases # también creamos las variables W y b para el entrenamiento W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.ones([10])) # por último, construimos el modelo pred = activation_function(tf.matmul(x, W) + b) # definimos nuestra función de pérdidas: en este caso, la cros-entropía # a veces la llaman loss, a veces cost: es lo mismo # cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1)) cost = tf.reduce_mean(tf.squared_difference(pred, y)) # calculamos los gradientes (gradient descent) grad_W, grad_b = tf.gradients(xs=[W, b], ys=cost) # definimos las operaciones para actualizar los pesos con los gradientes calculados # e implementamos el learning rate decay new_W = W.assign(W - learning_rate * (1-lr_decay) * grad_W) new_b = b.assign(b - learning_rate * (1-lr_decay) * grad_b) # inicializamos las variables init = tf.global_variables_initializer() # para almacenar el histórico de costes costs = [] # inicializamos current_lr current_lr = learning_rate # empezamos la sesión with tf.Session() as sess: sess.run(init) # entrenamiento de nuestra red for epoch in range(n_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) # y si en vez de actualizar los pesos para cada imagen, ¿lo hacemos # de X en X imágenes? for i in range(total_batch): batch_xs, batch_ys = mnist.train.next_batch(batch_size) # ejecutamos la optimización Wc, bc, c = sess.run([new_W, new_b ,cost], feed_dict={x: batch_xs, y: batch_ys}) # calculamos el coste teniendo en cuenta los batches que hay avg_cost += c / total_batch # actualizamos el learning_rate igual que lo hace tensorflow current_lr = current_lr * (1-lr_decay) # guardamos nuestro coste en el histórico costs.append(avg_cost) # Imprimimos las iteraciones # current_lr = learning_rate * (1-lr_decay) ** (epoch * batch_size + i) print("[{}] cost: {} lr: {}".format(epoch, avg_cost, current_lr)) print("Entrenamiento finalizado!!") # comprobamos lo que ha aprendido nuestra red correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1)) # calculamos el accuracy (precisión) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# veamos nuestra función de pérdidas con respecto a las épocas ejecutadas
plt.plot(np.arange(0, n_epochs), costs)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
In [ ]:
# probamos la tanh, bias = 1 y loss_fn = mse activation_function = tf.nn.tanh learning_rate = 0.1 lr_decay = 1e-3 n_epochs = 10 batch_size = 128 train_network_decay_fnact_b1_mse(activation_function, learning_rate, lr_decay, batch_size, n_epochs)
[0] cost: 0.07838331333129271 lr: 0.0999 [1] cost: 0.056300459876830265 lr: 0.0998001 [2] cost: 0.04908392807612051 lr: 0.0997002999 [3] cost: 0.04571573170540215 lr: 0.0996005996001 [4] cost: 0.04431915201576719 lr: 0.0995009990004999 [5] cost: 0.0434570159580741 lr: 0.0994014980014994 [6] cost: 0.04306625371629542 lr: 0.0993020965034979 [7] cost: 0.042781398360267966 lr: 0.09920279440699441 [8] cost: 0.04261634539647811 lr: 0.09910359161258742 [9] cost: 0.04248487542976031 lr: 0.09900448802097483 Entrenamiento finalizado!! Accuracy: 0.8551
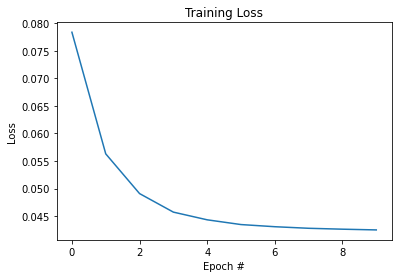
Hay 3 cosas que van íntimamente ligadas y de las que debemos ocuparnos para encontrar una buena configuración:
- La función de activación.
- La función de pérdidas.
- La inicialización de los pesos y bias.
En el desarrollo de este post, te has podido familiarizar con el desarrollo de la función de pérdida vs función de activación para el manejo de los macrodatos dentro del Deep Learning. Por ello, ahora confiamos en que sepas cómo instaurar cada una de las funciones, puesto que estas son de suma importancia para tu procesamiento del Big Data.
Para ayudarte a profundizar en este tema y muchos otros, desde KeepCoding te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. ¡No dudes en apuntarte para convertirte en un profesional en pocos meses!











