La función Q(z) en estadística Big Data forma parte de las alternativas con las que cuenta un estudio estadístico, de manera que, como un buen data scientist, debes conocer cada una de ellas para elegir asertivamente y potenciar los resultados arrojados por el estudio estadístico de los datos.
En consecuencia, una vez se hayan llevado a cabo estas tareas podrás facilitar la visualización de los datos, la toma de decisiones y las rutas de planeación que ayuden a la organización para la que trabajes. En definitiva, si la función Q(z) en estadística Big Data se encuentra en tus posibles soluciones, ¡quédate hasta el final de este post!
Una de las primeras cuestiones a tener en cuenta es que este tipo de función requiere de otros conocimientos base y otros que lo complementan como el gráfico Q-Q. Por esta razón, en este artículo, te explicamos todo lo relacionado con lo que es la función Q(z) en estadística Big Data.
Distribución gaussiana en estadística
Pues bien, en primer lugar, la función Q(z) en estadística Big Data forma parte de lo que se conoce como la distribución normal o gaussiana. Esta es, posiblemente, la distribución de probabilidad más utilizada, precisamente, porque es la distribución básica para un análisis estadístico.
La importancia de esta distribución, además, radica en que cuenta con el teorema central del límite.
Por otra parte, la función de densidad de probabilidad es:
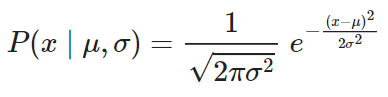
Mientras que la función acumulativa de probabilidad no tiene una forma explícita:
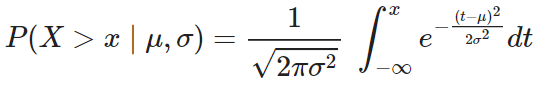
¿Qué es la función Q(z) en estadística Big Data?
Entrando en materia, la función Q(z) en estadística Big Data hace referencia a la probabilidad que existe de que una variable aleatoria gaussiana obtenga un valor mayor que x desviaciones típicas por encima de la media.
Por otra parte, para llevara cabo este cálculo se parte de la siguiente fórmula:
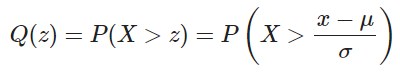
Por ejemplo, para ilustrar cómo funciona, podrás suponer que la media que se está abordando es igual a 0, entonces, su fórmula y sus resultados se presentarían de la siguiente forma:
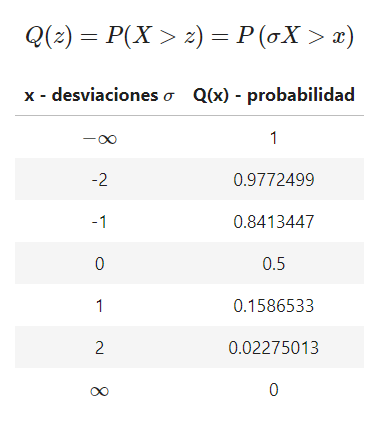
Ahora bien, por medio de esta función Q(z) en estadística Big Data también podrás hacer uso de las operaciones pnorm y qnorm en el lenguaje de programación R.
print("En R se calcula con pnorm:")
pnorm(1,lower.tail = F)
print("La inversa se calcula con qnorm:")
qnorm(0.158655,lower.tail = F)
[1] «En R se calcula con pnorm:»
0.158655253931457
[1] «La inversa se calcula con qnorm:»
1.00000104943105
require(ggplot2)
options(repr.plot.height=4,repr.plot.width=6)
plot_qz<-function(l1,l2){
qnorm1sd<-function(x){
out<-dnorm(x)
out[x< l1]<-NA
out
}
qnorm05sd<-function(x){
out<-dnorm(x)
out[x<l2]<-NA
out
}
qval1<-round(pnorm(l1,lower.tail = F),3)
qval2<-round(pnorm(l2,lower.tail = F),3)
xdf<-data.frame(z=c(-4,4))
ggplot(xdf,aes(x=z))+stat_function(fun=dnorm,args = list(mean = 0, sd=1))+
stat_function(fun=qnorm1sd, geom="area",fill="red")+
geom_text(x=l1+1,y=dnorm(l1),size=4,label=paste0("Q(",l1,")=",qval1))+
stat_function(fun=qnorm05sd, geom="area",fill="green",alpha=0.2)+
geom_text(x=l2+1,y=dnorm(l2),size=4,label=paste0("Q(",l2,")=",qval2))
}
l1<-1 l2<- -0.4 plot_qz(l1,l2)
Por último, la esquematización de la función Q(z) en estadística Big Data se produce a través del gráfico Q-Q, como se ilustra a continuación:
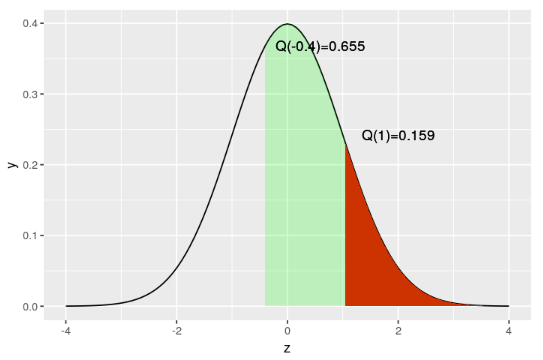
Gráfico Q-Q y la función Q(z)
El grafico Q-Q es el predilecto para la función Q(z) en estadística Big Data, ya que se utiliza para comparar dos distribuciones pintando sus percentiles una contra la otra y generalmente se utiliza para comparar si una variable sigue una distribución gaussiana.
x<-seq(-4,4,length.out=1000) plot(x,pnorm(x,lower.tail = F),t="l",ylab="Q(x) - probabilidad",xlab="x - número de desviaciones típicas sobre la media") grid() # Es equivalente a: plot(x,1-pnorm(x),t="l")
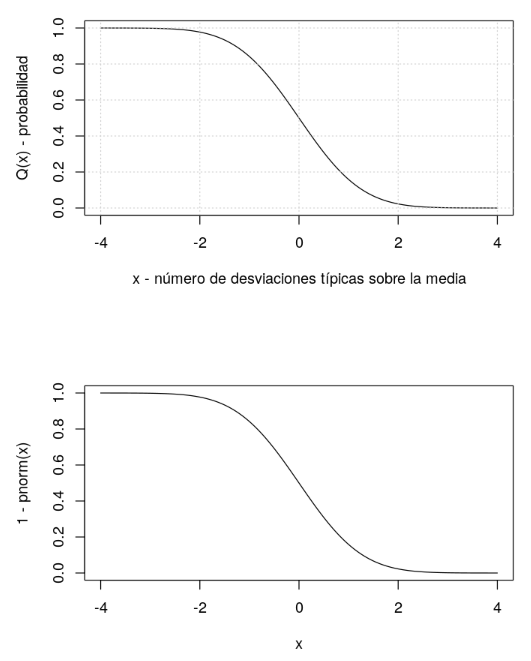
numSamples<-10
#Empezamos con una variable aleatoria ordenada
var_random <-sort(runif(numSamples,min=-5,max=5))
#calculamos su probabilidad de que P(X>x)
p = ((numSamples-1):0)/numSamples
#Basandonos en esta probabilidad, calculamos cual sería su valor si fuera gaussiana
z<-qnorm(p,lower.tail = F)
matrix(c(var_random,p,z),nrow=3,byrow = T,
dimnames=list(c("x","P(X>x) o Q(x)","valor esperado de x si fuera gaussiana"),NULL))

#plot(p,var_random)
#El gráfico QQ sería:
plot(z,var_random,
xlab="número de desviaciones típicas sobre la media teórica",
ylab="valores reales")
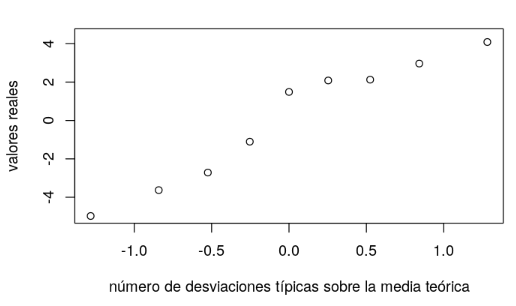
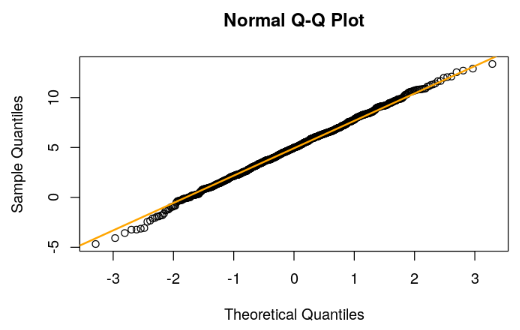
Evidentemente, el gráfico Q-Q de una variable gaussiana es una línea recta:
numSamples<-1000
gauss_random <-sort(rnorm(numSamples,mean=5,sd=3))
p = ((numSamples-1):0)/numSamples
z<-qnorm(p,lower.tail = F)
plot(z,gauss_random,
xlab="número de desviaciones típicas sobre la media teoórica",
ylab="valores reales")
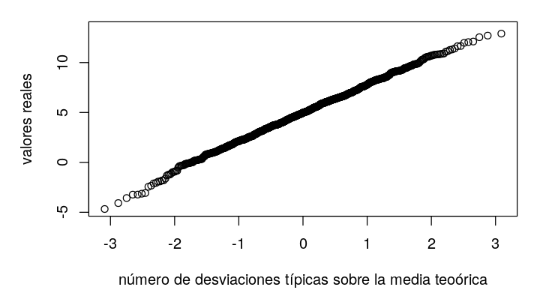
Existe una función para hacer esto mismo:
qqnorm(gauss_random) qqline(gauss_random, col = 'orange', lwd =2)
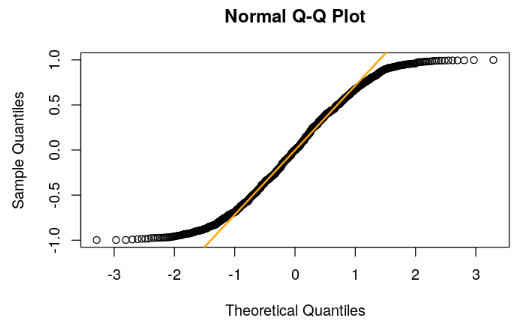
unif1<-subset(myRandomDataFrame,numFunctions==1)$val qqnorm(unif1) qqline(unif1, col = 'orange', lwd =2)
¿Cómo continuar aprendiendo sobre el Big Data?
En el desarrollo de este post te hemos expuesto todo lo relacionado a Función Q(z) en estadística Big Data como parte de una distribución normal para el desarrollo de un análisis estadístico de los macrodatos. No obstante, este tipo de conocimientos deben adecuarse a tu tipo de interés en los datos procesados.
Si no sabes cómo seguir con el proceso, te recomendamos echar una vistazo a nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, puesto que, por medio de este, podrás desarrollar todas tus habilidades en el aprendizaje de las herramientas y lenguajes principales en el mundo del manejo de los macrodatos. Además, te especializarás en una gran cantidad de temas relacionados con la forma en la que funcionan los tipos de distribución, como la uniforme, de bernoulli, binomial, de Poisson, exponencial, gaussiana, Chi-cuadrado, T-student y Betav. Durante todo este proceso también contarás con material extra, webinars y cursos que potenciarán lo aprendido en el bootcamp. ¿A qué estás esperando para empezar?



