¿Sabías que existe en machine learning algo denominado importancia de las variables en los algoritmos basados en árboles? Como su nombre indica, esta es una propiedad muy interesante de los algoritmos basados en árboles y consiste en medir la importancia de las variables según diferentes factores.
En este artículo, te mostramos cómo puedes calcular la importancia de las variables en los algoritmos basados en árboles.
Importancia de las variables en los algoritmos basados en árboles
Veamos:
importances = bagModel.feature_importances_
importances / np.max (importances)
indices = np.argsort (importances) [ : : - 1]
plt.figure (figsize = (10, 10))
plt.barh (range (X_train.shape [1]), importances [indices]) plt.yticks (range (X_train.shape[1]), features [indices])
plt.show ()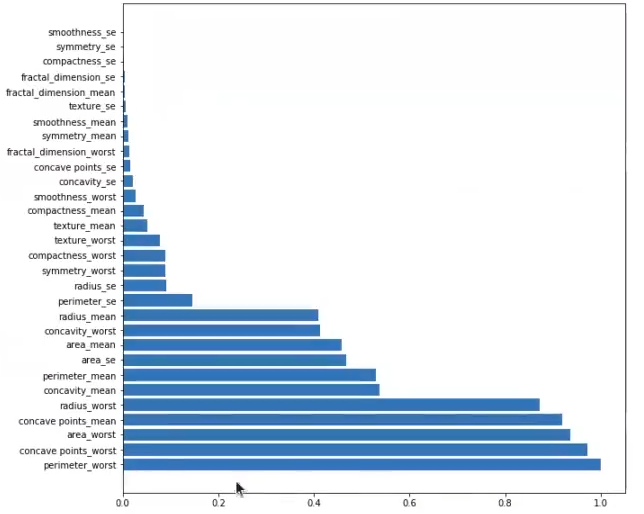
Esta gráfica nos muestra cuál es, de 0 a 1, la importancia de las variables en los algoritmos basados en árboles.
Aquí vemos cómo tenemos un primer grupo de selectores que parecen más relevantes, como radius worst, concave points mean, area worst, concave points worst y perimeter worst.
El segundo grupo, aunque menos relevante que el primero, sigue teniendo bastante importancia.
Los demás grupos tienen muy poca relevancia.
La información que tenemos aquí podemos cogerla y aplicarla en un árbol individual, pero lo que sacamos de un árbol individual es mucho menos concluyente que lo que sacamos de otras estructuras o modelos, como un random forest.
Veamos cómo quedaría un árbol individual:
from sklearn.tree import export graphviz
import graphviz
tree_dot = export_graphviz (treeModel, out_file = None, feature_names = features, class names = ['B', 'M'], filled = True, rounded = True, special_characters = True)
graph = graphviz.Source (tree_dot)
graph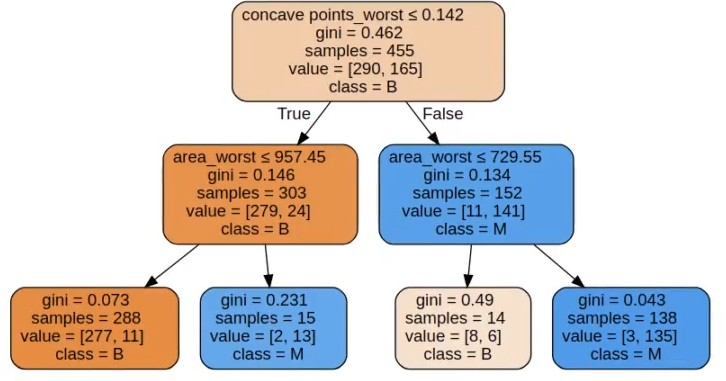
importances = treeModel. feature importances
importances = importances / np.max (importances)
indices = np.argsort (importances) [ : : - ]
plt.figure (figsize = (10, 10))
plt.barh (range (X_train.shape [1]), importances [indices]) plt.yticks (range (X_train.shape[1]), features [indices])
plt.show()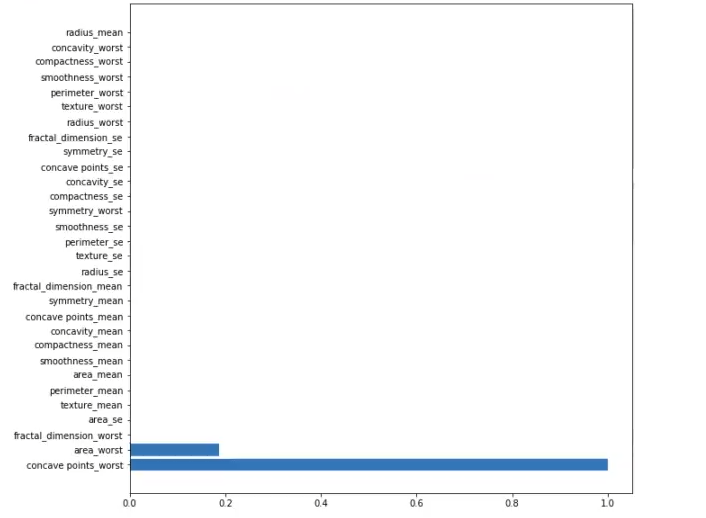
Como puedes observar, la importancia de las variables en los algoritmos basados en árboles, específicamente en este árbol, no tiene mucho sentido. Aquí parece que solo hay una variable que importa y otra que es ligeramente relevante; el resto no tienen ninguna importancia en absoluto, ya que ni siquiera aparecen en la gráfica.
Este resultado tiene mucho sentido, ya que el árbol anterior tiene una profundidad de 2 y está usando la variable concave points worst y la variable area worst. Esa es la razón por la que solo esas dos variables tienen importancia y el resto no: porque el árbol no las está usando.
En comparación con la gráfica anterior, vemos sustanciales diferencias. No es lo mismo calcular la importancia de las variables en los algoritmos basados en árboles con un solo árbol, que con, por ejemplo, 200. Este último caso tiende a ser mucho más significativo.
Volviendo a nuestro ejercicio, al utilizar este ranking podemos hacer selección de características.
from sklearn.model_selection import KFold
N, Nfeatures = x_train.shape
rf = RandomForestClassifier (max depth = maxDepthOptimo, n_estimators = 200, max_features = 'sqrt')
kf = KFoldin_splits =10, shuffle = True, random_state = 1)
CV_error = [ ]
CV_std = [ ]
for nfeatures in range (Nfeatures, 0, -1):
error_i = [ ]
for idxTrain, idxVal in kf.split (x_train):
Xt = X_train [idxTrain, :]
yt = y_train [idxTrain]
Xv = X_train [idxVal,:]
yv = y_train [idxVal]
rf.fit(xt,yt)
ranking = rf.feature_importances
indices = np.argsort (ranking) [ : : -1]
selected = indices [0: (Nfeatures - nfeatures + 1)]
Xs = Xt [ : , selected]
rf.fit (xs, yt)
error = (1.0 - rf.score (Xv [ : , selected], yv))
error_i.append (error)
cv_error.append (np.mean (error_i))
cv_std.append (np.std (error_i))
print ('# features + str (len (selected)) + str (np.mean (error_i)) + '+/-' + str (np.std (error_i)))# features 1 error 0.10106280193236716 +/- 0.01999766608707034
# features 2 error 0.07478260869565219 +/- 0.024776345603295568
# features 3 error 0.07038647342995168 +/- 0.02183558847361098
# features 4 error 0.0704830917874396 +/- 0.024237009142968093
# features 5 error 0.05927536231884055 +/- 0.017090869840982296
plt.plot (range (1, Nfeatures + 1, 1), cv_error, '-o')
plt.errorbar (range (1, Nfeatures + 1, 1), cv_error, yerr = cv_std, fmt = 'o')
plt.xlabel ('# features')
plt.ylabel ('CV error')
plt.show ()Aunque quizás es más recomendable usar regularización Lasso para algoritmos de aprendizaje en clasificación, también podemos usar la opción que aquí proponemos.
La importancia de las variables en los algoritmos basados en árboles está dada, principalmente, por el Gini. No obstante, existen ocasiones en las que también se puede usar la entropía.
Lo que hace es, a través de los 200, 500 o el número de árboles que tengas, evaluar la mejora que se ha producido en cada uno de los splits que usan esa variable.
La importancia de las variables en los algoritmos basados en árboles es una temática de gran relevancia en el estudio del Big Data. Si quieres continuar aprendiendo sobre este y otros temas relacionados con una de las disciplinas mejor pagadas de la actualidad, tenemos para ti el Bootcamp Big Data, una formación intensiva en la que adquirirás fundamentos teóricos y prácticos que te permitirán incursionar en un mercado laboral lleno de oportunidades. ¡No desaproveches esta oportunidad y solicita más información ahora!











