Los intervalos de confianza en estadística Big Data forman parte fundamental del desarrollo de un estudio estadístico para determinada población de datos, puesto que estos potencian o desmeritan el grado de confianza que se puede otorgar a un procesamiento de los datos y sus resultados arrojados.
En este post, te compartimos algunos de los intervalos de confianza en estadística Big Data.
Intervalos de confianza en estadística Big Data
Los intervalos de confianza en estadística Big Data hacen referencia al acierto según el margen de error que maneje determinado estudio estadístico de los datos.
Sin embargo, existen diferentes tipos y, a continuación, te compartimos algunos de los intervalos de confianza en estadística Big Data más utilizados.
Intervalo de confianza para proporciones
Imagina que has realizado η experimentos independientes, cada experimento puede caber con éxito con una probabilidad ρ.
Si de los η experimentos realizados, tienes η experimentos que acaban en éxito, se estima la probabilidad como:
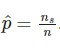
Pero está claro que no se tiene la misma confianza en la proporción si hacemos dos experimentos o 2000, aunque ambos ofrezcan una ρ = 0.5. Observa esta proporción:
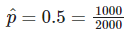
El ejemplo anterior parece tener una mayor confianza que el siguiente:
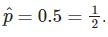
A calcular el margen de error de esta probabilidad se le llama credibilidad de una proporción o probabilidades de cobertura.
Aproximación gaussiana asintótica
También conocida como método de Wald, el margen de error es simétrico y viene dado por la fórmula:
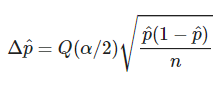
El problema es que esta fórmula puede llevar a dos aberraciones:
- Para bajas proporciones, cuando η es bajo, el límite inferior puede ser negativo (Δ ρ > ρ). Para ρ cercano a 1, el límite superior puede exceder 1.
- Intervalo Δ ρ > 0 ocurre cuando p=0 o p=1. Aunque el uso del factor corrector de continuidad puede solucionarlo:
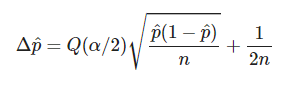
Intervalo de confianza de proporción binominal
La distribución binomial es una generalización de la distribución de Bernoulli para nn sucesos independientes, cada uno de los cuales tiene dos posibles resultados Sí/No con probabilidad pp.
Ejemplo: tirar al aire 20 monedas y mirar cuál es la probabilidad de que salga cara 10 veces.
Variables que definen la distribución:
- p – probabilidad de éxito de un caso individual.
- n – número de eventos totales que se desean medir.
- k – número de eventos donde ha salido Sí.
# Ejemplo: Tiramos 20 monedas NO TRUCADAS al aire y miramos la probabilidad de que en 10 salga cara dbinom(x=10, size=20, prob=0.5)
num_caras <- 0:20 prob<-dbinom(num_caras, size=20, prob=0.5) #prob<-pbinom(num_caras, size=20, prob=0.5) plot(num_caras,prob)
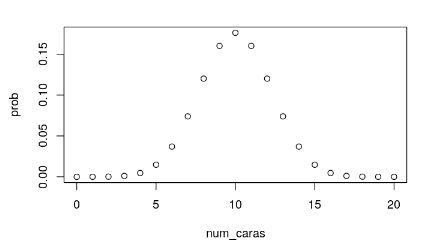
En este caso, el intervalo de confianza no es simétrico y viene dado por la fórmula:
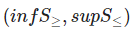
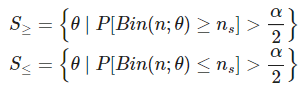
Funciones en R
Esto se puede calcular en R ejecutando la función binom.test:
binom.test(ns,n)
Exact binomial test
data: ns and n
number of successes = 323, number of trials = 1000, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.2940739 0.3529724
sample estimates:
probability of success
0.323
ns<-10
nt<-20
bt<-binom.test(ns,nt)
bt
df_binom_test<-data.frame(prob_mean=seq(0,1,length.out=100))
df_binom_test$p<-dbinom(ns,nt,df_binom_test$prob_mean)
fillarea<-function(x){
out<-dbinom(ns,nt,x)
out[x<bt$conf.int[1]]<-NA
out[x>bt$conf.int[2]]<-NA
out
}
options(repr.plot.height=4,repr.plot.width=6)
library(ggplot2)
ggplot(df_binom_test,aes(x=prob_mean,y=p))+geom_line()+
stat_function(fun=fillarea, geom="area",fill="green",alpha=0.2)
Exact binomial test
data: ns and nt
number of successes = 10, number of trials = 20, p-value = 1
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.2719578 0.7280422
sample estimates:
probability of success
0.5
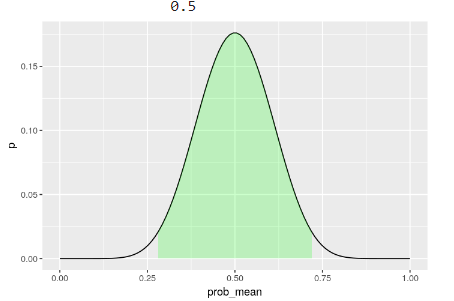
La probabilidad más alta es 0.5. Si supones que la probabilidad del evento es 0.5, es decir, el valor ns/nt, tienes:
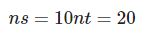
Entonces, sabes que un 17% de las veces que en las que tengas 20 eventos, habrá exactamente 10 eventos positivos.
dbinom(ns,nt,0.5)
Intervalo de confianza usando función Beta
La fórmula de su densidad de probabilidad recuerda mucho a la de Binomial. Recuerda la fórmula de la función de distribución de Binomial:
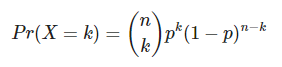
La función de densidad de probabilidad de la función beta es:
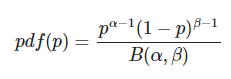
Donde:
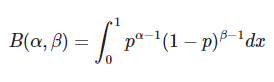
Estimadores media (μ) y varianza (σ²):

La moda sería:
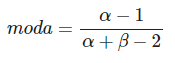
Puedes pensar en:
- α-1 como el número de éxitos.
- β-1 como el número de fallos.
En este post te hemos explicado cómo funcionan los intervalos de confianza en estadística Big Data y sus respectivas cualidades, de manera que ahora los puedes tener en cuenta a la hora de realizar un estudio estadístico del Big Data. No obstante, ¡todavía queda mucho más por aprender sobre el manejo de los macrodatos!
Desde KeepCodging, te traemos el Bootcamp Big Data y Data Science Full Stack, gracias al que podrás aprender mucho más sobre los intervalos de confianza en estadística Big Data y, en general, sobre los sistemas y herramientas más importantes en el universo del Big Data. De la mano de profesionales y en menos de nueve meses, te podrás convertir en todo un experto y conocer e identificar las alternativas de gestión de datos más apropiadas para los estudios de los macrodatos. ¡No dudes en solicitar más información e inscríbete ahora!











