El learning rate en Deep Learning es uno de los procesos que forman parte de la optimización de hiperparámetros en Deep Learning.

En efecto, de entre todos los hiperparámetros, el learning rate y el batch size son dos parámetros directamente relacionados con el algoritmo del gradient descent.

En este post, te presentamos que es el learning rate en Deep Learning.

Learning rate en Deep Learning

Para aprender sobre el learning rate en Deep Learning, te recordamos que la forma de actualizar los pesos es mediante estas fórmulas:

Lo que multiplica al ∂Etotal/∂wn, llamado η, es el learning rate, que indica la importancia que le damos al error para actualizar cada peso, es decir, la rapidez o cómo de abruptos son los cambios en los pesos.

Así, un η muy alto, hará que los cambios en los pesos sean muy grandes de una iteración a otra, lo que genera el problema de que podemos llegar a saltarnos nuestro mínimo.

Con esta imagen podrás verlo mejor:

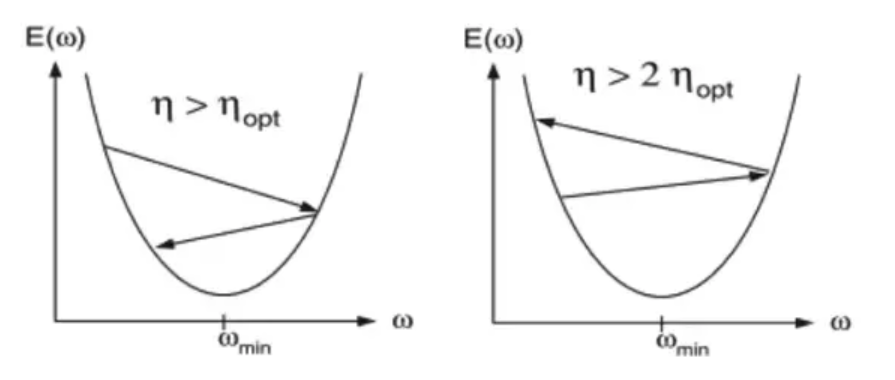
Otra posibilidad es establecer un η muy bajo, lo que haría que nuestra red necesitara muchísimas épocas para llegar a un mínimo aceptable. Además, correríamos el riesgo de quedarnos atrapados en un mínimo peor del mejor que podríamos conseguir con un η más alto.

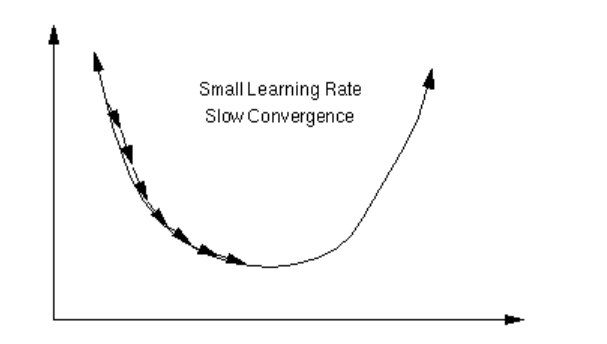
Vamos a hacer un pequeño inciso para hablar sobre los mínimos: lo que conseguimos con una red neuronal, normalmente, no es alcanzar el mínimo global de nuestra función, sino que alcanzamos un mínimo local lo suficientemente bueno como para realizar correctamente la tarea que estamos desarrollando.

Tras haber aclarado esto, queda patente lo importante que es conseguir un learning rate adecuado. Fíjate en esta imagen:

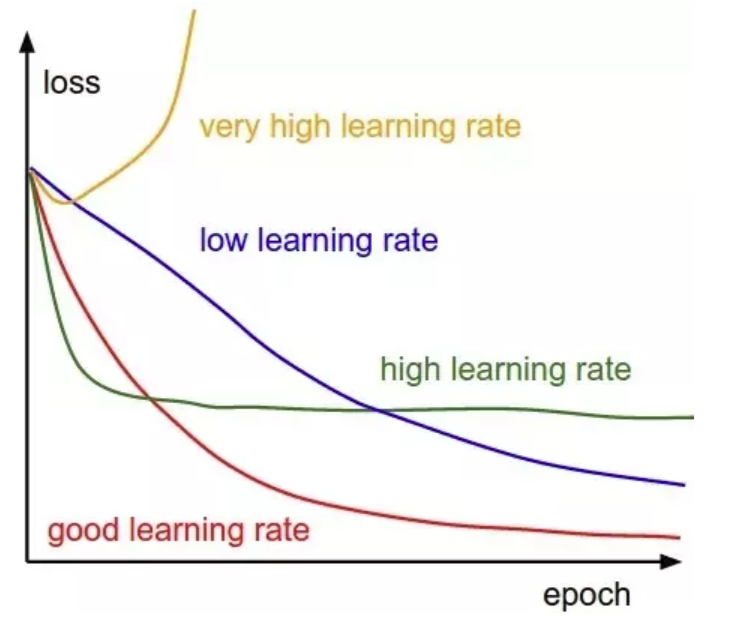
Lo que queremos es un learning rate en Deep Learning óptimo que nos permita ir reduciendo el error conforme van pasando las épocas hasta llegar a nuestro mínimo buscado. En la gráfica, este learning rate sería la línea roja. ¿Y cómo conseguimos que nuestro learning rate sea óptimo?

Una opción muy utilizada es aplicar un decrecimiento o decay a nuestro learning rate conforme va disminuyendo la función de pérdidas (lo que indica que estamos llegando al mínimo buscado).

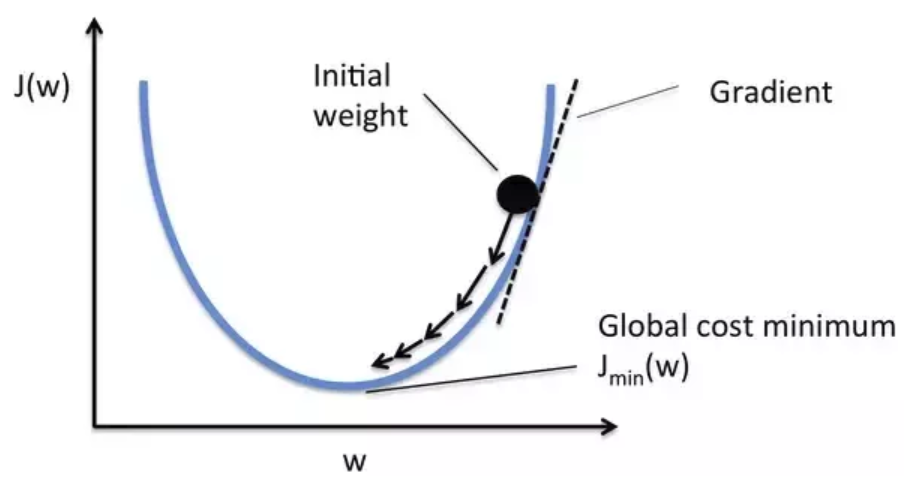
Vamos a ver cómo se comportaría la última red que implementamos (la que trabajaba con el MNIST) con diferentes learning rates:

# recuerda elegir TF 1.x o no te funcionarán los ejemplos:
%tensorflow_version 1.x

TensorFlow 1.x selected.

# Ejemplos learning rate

# En primer lugar, hacemos los imports necesarios y después definimos una 
# función que creará y entrenará la red

# imports necesarios
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf

# importamos el dataset MNIST y cargamos los datos
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

# Definimos la función para entrenar nuestra red con los parámetros deseados
def train_network(learning_rate, batch_size, n_epochs):
  
  # creamos los contenedores para nuestras entradas y salidas
  x = tf.placeholder(tf.float32, [None, 784]) # imágenes del mnist: 28*28=784
  y = tf.placeholder(tf.float32, [None, 10]) # número indicando la clase 0-9 => 10 clases

  # y creamos las variables W y b para el entrenamiento
  W = tf.Variable(tf.zeros([784, 10]))
  b = tf.Variable(tf.zeros([10]))

  # Por último, construimos el modelo
  pred = tf.nn.softmax(tf.matmul(x, W) + b)

  # Ahora, definimos nuestra función de pérdidas: esta vez, la cros-entropía
  # a veces la llaman loss, a veces cost => es lo mismo
  cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))

  # Calculamos los gradientes (gradient descent)
  grad_W, grad_b = tf.gradients(xs=[W, b], ys=cost)

  # Definimos las operaciones para actualizar los pesos con los gradientes calculados
  # y el learning rate
  new_W = W.assign(W - learning_rate * grad_W)
  new_b = b.assign(b - learning_rate * grad_b)

  # Inicializamos las variables
  init = tf.global_variables_initializer()
  
  # para almacenar el histórico de costes
  costs = []
  # empezamos la sesión
  with tf.Session() as sess:
      sess.run(init)
# entrenamiento de nuestra red
      for epoch in range(n_epochs):
          avg_cost = 0.
          total_batch = int(mnist.train.num_examples/batch_size)

          # ¿Y si en vez de actualizar los pesos para cada imagen, lo hacemos
          # de X en X imágenes?
          for i in range(total_batch):
              batch_xs, batch_ys = mnist.train.next_batch(batch_size)

              # ejecutamos la optimización
              _, _, c = sess.run([new_W, new_b ,cost], feed_dict={x: batch_xs,
                                                         y: batch_ys})

              # calculamos el coste teniendo en cuenta los batches que hay
              avg_cost += c / total_batch

          # guardamos nuestro coste en el histórico
          costs.append(avg_cost)
          
          # Imprimimos las iteraciones
          print("[{}] cost: {}".format(epoch, avg_cost))

      print("Entrenamiento finalizado!!")

      # comprobamos lo que ha aprendido nuestra red
      correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))

      # calculamos el accuracy (precisión)
      accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
      print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
# Veamos nuestra función de pérdidas con respecto a las épocas ejecutadas
  plt.plot(np.arange(0, n_epochs), costs)
  plt.title("Training Loss")
  plt.xlabel("Epoch #")
  plt.ylabel("Loss")

Por último, los valores típicos de learning rate en Deep Learning suelen ser:

0.1
0.01
0.001

En este post, te hemos expuesto qué es el learning rate en Deep Learning para el desarrollo de las redes neuronales profundas.

Desde KeepCodging, te traemos el Bootcamp Big Data, gracias al que podrás aprender mucho más sobre el learning rate en Deep Learning, así como sobre los sistemas y herramientas más importantes en el universo del Big Data. ¡No dudes en solicitar más información e inscríbete ahora!