Para medir la calidad de un clúster se puede proceder de varios modos. Partimos del hecho de que los objetos del dataset se pueden comprender fácilmente y cumplen los objetivos fundamentales y características cualitativas y cuantitativas de un buen clúster, es decir, un clúster de calidad.
Medir la calidad de un clúster
Lo que buscamos con medir la calidad de un clúster es que los elementos del mismo estén lo más cerca posible gracias a la agrupación, entre otras cosas, de los tipos de datos.
A su vez, lo que se busca es que la separación entre un clúster y el destino sea lo más ancha posible; cuanto más grandes sean las separaciones entre clústers obtenidos, mejor.
Un clúster tiene que cumplir dos propiedades:
- Los elementos dentro de un mismo grupo tienen que estar lo más cerca posible entre sí. La distancia media intraclúster tiene que ser baja.
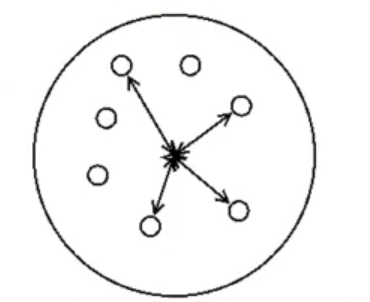
- Los elementos de distintos grupos tienen que estar lo más lejos posible uno de otro. La distancia media interclúster tiene que ser alta.
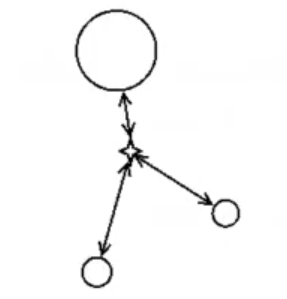
Medir la calidad de un clúster
Una forma de medir la calidad de un clúster es con el SSE (Sum Square Error):
- SSEIntra: se define para cada grupo. Es la suma de distancias al cuadrado entre los puntos de un clúster y el centroide.
- SSEInter: se define para todos. Es la suma de las distancias al cuadrado entre los centroides de un clúster (ponderado al número de elementos del clúster) y el centroide de los centroides.
- SSEtotal : SSEInter + ∑ SSEIntra
Del SSE se desprende el ratio, otra forma de medir la calidad de un clúster:
SSEInter
—————-
SSEtotal
Cuanto más cercano a 1, mejor es la división entre clústeres.
paste ("SSE intra: ", paste (round (myclust$withinss), collapse = ", "))
paste ("SSE inter : ", myclust$betweenss)
paste ("5SE total : ", myclust$totss)
paste ("SSE total : ", sum(myclust$withinss) + myclust$betweenss)‘SSE intra: 2013, 767, 1688’
A partir de los cálculos que podemos hacer con R para medir la calidad de un clúster, podemos decir que de todos los grupos el segundo es el mejor.
‘SSE inter: 21662.6017339349’
‘SSE total: 26130.1980286569’
‘SSE total: 26130.1980286569’
sse_per_cluser <- function (mydata_all, group, centroids) {
ssq <- rep (NA, nrow (centroids))
for (k in 1 : nrow (centroids)) {
mydata <- mydata_all group == k, ]
h <- 0
for (i in 1 : nrow (mydata)) {
h <- h + sum ((mydata [i, ] - centroids [k, ]) ^ 2)
}
ssq [k] <- h
}
ssq
}
#sse_per_cluster (df, group, centroids)
sse_per_cluster (df, myclust$cluster, myclust$centers)2012.8726250961 . 766.931551845045 . 1687.73211778088
sse betweeness <- function (group, centroids) {
sum ((centroids [group, 1] - mean (centroids [group, 1])) ^ 2)+
sum ((centroids [group, 2] - mean (centroids [group, 2])) ^ 2)
}
#sse_betweeness (group, centroids)
sse_betweeness (myclust$cluster, myclust$centers)21662.6617339349
Determinando el número óptimo de clústeres para k-means
No existe una regla fija para determinar el número de grupos. Podemos pintar cómo evoluciona el error cuadrático y, cuando deje de mejorar rápidamente, establecer el número de clústeres.
Lo que se hace con k-means es probar con diferentes números de clústeres. Vamos a calcular el betweenss entre el total.
Lo que queremos es encontrar codos. Si observamos la gráfica, observamos que entre 0 y 3 hay un codo y, a partir de ahí, parece que la gráfica no aumenta mucho más. Así podríamos deducir que el valor óptimo de clústeres es 3.
q <- c ()
for (k in 1 : 8) {
myclust <- kmeans (df, k)
q [k] <- myclust$betweenss / myclust$totss
}
plot(q)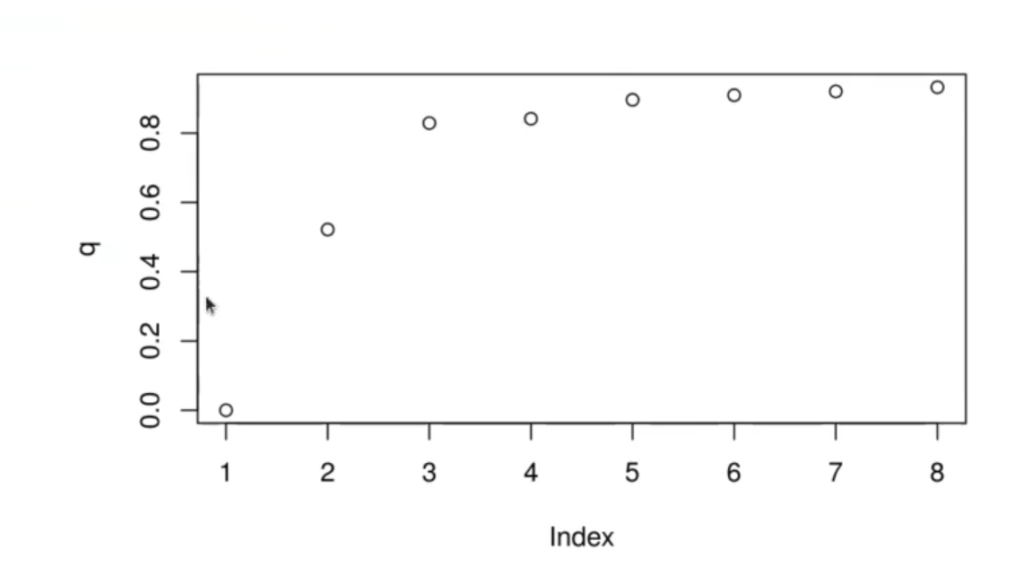
Otra forma es mirando el ∑ SSEIntra:
q <- c ()
for (k in 1 : 8) {
myclust <- kmeans (df, k)
q [k] <- sum (myclust$withinss)
}
plot (q)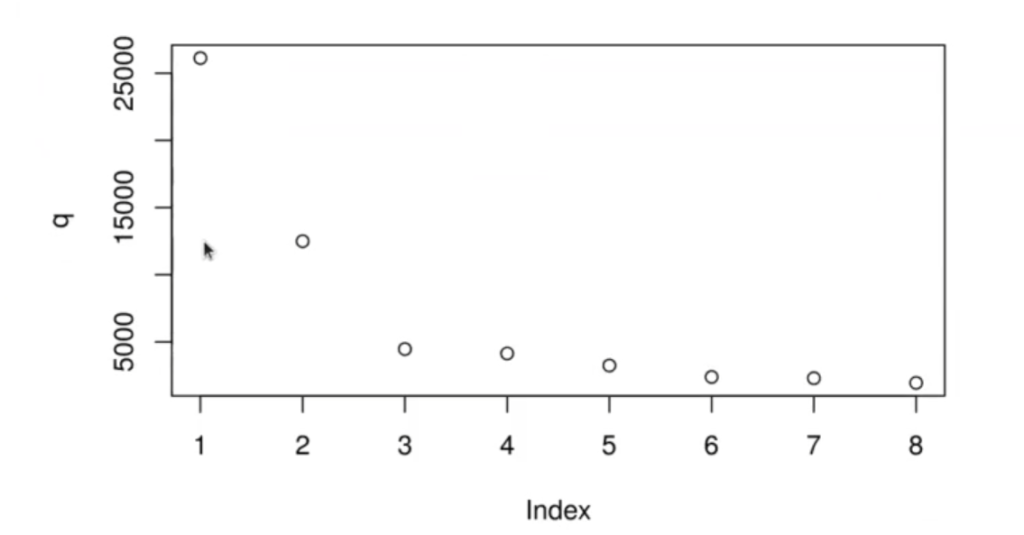
Cuanto más bajo sea el intra, mejor. Hacemos lo mismo que con el ejemplo anterior: buscamos un codo y el punto en el que se estabilice el codo es el valor máximo de clústeres que debe haber. En nuestro caso ese valor vuelve a ser 3.
Tener en cuenta las formas de medir la calidad de un clúster es de suma importancia para tener grupos de datos óptimos que nos permitan hacer análisis específicos y predicciones precisas.
Esta es solo una pequeña parte del amplio mundo del Big Data y el data mining.
Si quieres seguir aprendiendo, recuerda que tenemos disponible nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que, en muy poco tiempo, puedes adquirir todos los conocimientos necesarios para incursionar en uno de los mercados laborales más prolíficos en la actualidad. Estarás acompañado de los mejores profesionales en todo momento y, al finalizar, tendrás acceso de por vida a una amplia Bolsa de Talento. ¡Anímate y solicita más información!











