El descenso de gradientes es un algoritmo iterativo que se utiliza para encontrar un mínimo global, mínimo local o un máximo local de una función dada.
El método de descenso de gradientes es ampliamente usado en machine learning o aprendizaje automático y en deep learning, también llamado aprendizaje profundo. Lo que busca este método es crear algoritmos de optimización que permitan que la función de error y función de pérdida sean menores.
Tipos de descenso de gradientes
Existen diferentes tipos de descenso de gradientes que se pueden utilizar en Big Data y son muy diferentes entre sí. Estos son:
Descenso de gradientes por lotes
Calcula el error para cada ejemplo dentro del conjunto de datos de entrenamiento. Su mayor ventaja es su estabilidad a la hora de producir un gradiente de error y una convergencia.
Descenso de gradientes estocástico
Analiza los parámetros de cada ejemplo del entrenamiento, uno por uno. Una de sus mayores ventajas radica en sus constantes actualizaciones, lo que la convierte, a su vez, en una opción costosa. Se convierte en un arma de doble filo.
Descenso de gradientes por minilotes
Divide el conjunto de datos de entrenamiento en pequeños lotes y realiza una actualización para cada uno de ellos. Es una mezcla de lo mejor del descenso de gradientes estocástico y del descenso de gradientes por lotes.
Espacio vectorial
La mayor parte de las funciones a optimizar no toman como entrada un escalar, sino un vector. En este caso, el vector definirá un espacio en el cual habrá que encontrar el valor que produzca el mínimo valor.
Hasta este momento hemos visto la derivada de una función. Ahora, vamos a introducir el concepto de derivada parcial.
En una función ƒ : 
n -> la derivada parcial ∂/∂x ƒ(x->) mide como cambia ƒ(x->) en función de la variable xi; esto es la columna i-ésima del vector x->.
Por ejemplo, la derivada parcial respecto a x₁ es:
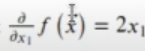
La derivada parcial respecto a x2 es:
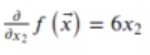
El gradiente es la derivada respecto al vector x->, que es una generalización multivariable de la derivada. Se denota con el símbolo Δƒ. El resultado es un vector, a diferencia de la derivada, cuyo resultado es un escalar.
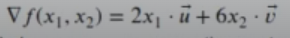
Aquí u-> y v-> son los vectores unitarios de las coordenadas dadas por x1 y x2, respectivamente.
El gradiente indica la dirección de máximo crecimiento de la función y su valor negativo indica la dirección de máximo de decrecimiento.
Así pues, el método de descenso de gradientes se basa en encontrar la dirección de máximo decrecimiento de la función y actualizar el valor de x-> en conformidad.
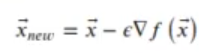
∈ es una constante, un hiperparámetro que hay que definir al principio de la iteración. Se conoce como tasa de aprendizaje (leaming rate). Un valor pequeño puede hacer que se necesiten muchas iteraciones para converger, un valor grande puede hacernos perder el máximo de la función.
El método de descenso de gradientes converge cuando todos los elementos del gradiente son cero (o muy próximos a cero).
El método de descenso de gradientes se considera un algoritmo de primer orden, porque utiliza información solo de la primera derivada. Nunca utiliza información de la segunda derivada.
A modo de ejemplo
Crearemos una función que nos calcule el gradiente:
In [77]: myfuncVector<- function(x) { x[1]^2+3*x[2]^2}
mygradient<- function(x,h, func){
c((func(c(x[1]+h, x[2]))-func(x))/h,
(func(c(x[1],x[2]+h))-func(x))/h) }
mygradient(c(4,3),0.001,myfuncVector)Los resultados de esta fórmula serían 8,00100000000725 y 18,0030000000002.
In [ ]: library(plotrix)
x_0 <- c(-9, -9)
delta <- 0.15
h<- 0.001
criterio_convergencia<-0.05
x_historico<- data.frame(x=x_0[1],y=x_0[2])
for (i in 1:100) {
g<- mygradient(x_0,h,myfuncVector)
if(abs(sum(g))<criterio_convergencia){
break;
}
x_new <- x_0 - g*delta
x_0 <- x_new
x_historico <- rbind(x_historico, data. frame(x=x_0[1],y=x_0[2]))
}Ya tenemos la fórmula que nos calcula el descenso de gradientes.
La función al mínimo está en 0. El 8 y el 18 son el gradiente en el punto 4,3; es hacia donde está apuntando la flecha de máximo gradiente:
mygradient(c(4,3),0.001,myfuncVector)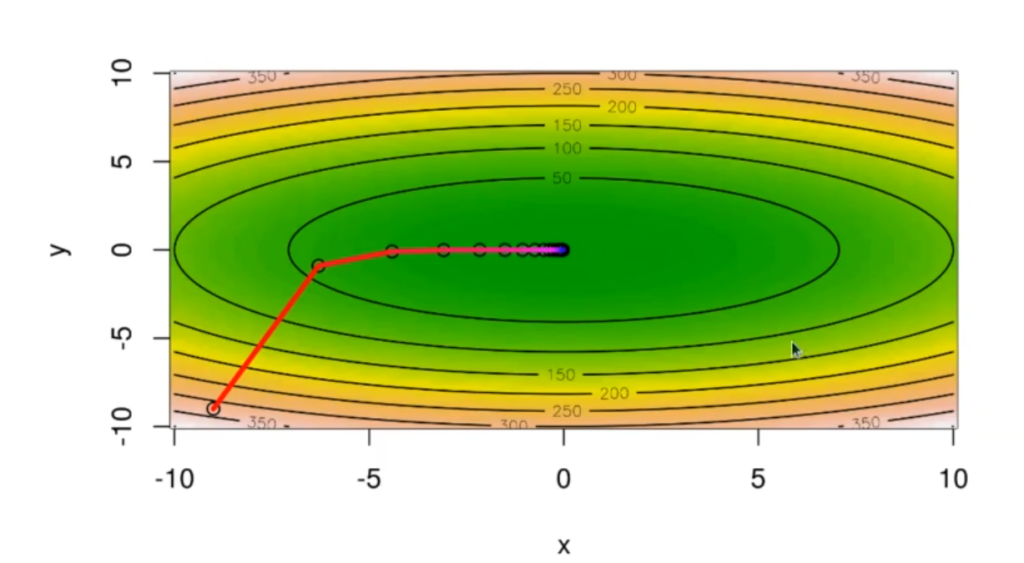
La gráfica que se pinta está es la de { x[1]^2+3*x[2]^2}.
Las que se ven en negro son las curvas de nivel. La gráfica nos está diciendo que, en el punto 4,3 (señalado con rojo), el gradiente va a apuntar hacia donde crece (señalado con azul).
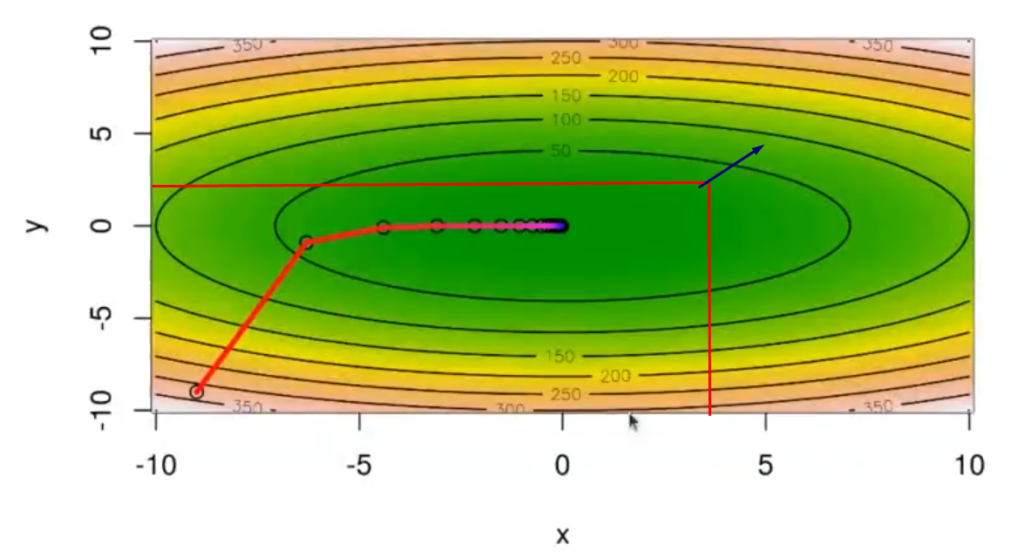
Así pues, el gradiente crece 8 puntos en x (horizontal) y 18 puntos en y (vertical). Cuando a este resultado lo restamos al valor de x, nos va a dar un valor que está más cercano a 0 que antes.
¿Qué sigue?
En este artículo hemos visto cómo implementar el método de descenso de gradientes en un análisis predictivo, pero falta mucho más por ver y conocer. Sigue revisando nuestros posts para seguir aprendiendo; aunque si lo que buscas es una formación intensiva que te abra las puertas del mercado laboral del sector IT, no puedes perderte nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Aprenderás de manera fácil y rápida todo lo que necesitas para convertirte en un gran profesional. ¡Pide información y cambia tu vida!
