Existen dos tipos de mínimos en data mining y, en general, en las matemáticas: el mínimo local y el mínimo global.
En este post, hablaremos un poco de ambos mínimos en data mining y veremos algunos ejemplos.
Mínimos en data mining: contextualización
¿Qué ocurre cuando tenemos una función con varios mínimos en data mining que son locales?
Las funciones que trataremos de minimizar muchas veces no serán funciones convexas como la que hemos visto, sino que podrán tener varios mínimos en data mining que son locales.
Es imposible garantizar que nuestro algoritmo de optimización acabará en un mínimo global, pero por lo menos nos tenemos que asegurar de que cae en un mínimo local con un valor lo suficientemente cercano al del mínimo global.
Veamos un ejemplo con la siguiente función:
In [31]: myfunc2<- function (x) {0.05*x^2+sin(x)}
x<-seq(-10,10, length.out = 100)
y<-myfunc2(x)
plot(x,y,t="l")In [32]: library(plotrix)
derivada_myfunc<-function (x, h, func) { (func(x+h)-func(x))/h }
x_0<--20
delta <- 1
#delta <- 3 #Cambiar delta
h<-0.001
criterio_convergencia<-0.5
x_historico<-c()In [ ]: x_new <- x_0 - derivada_myfunc(x_0, h, myfunc2) *delta
x 0 <- x_new
x_0
x_historico<-c(x_historico,x_0)
plot(x,y,t="l")
points (x_historico,myfunc2(x_historico),col="red")
color.scale.lines (x_historico, myfunc2 (x_historico), c(1,1,0) ,0,c(0,1,1), colvar=1:length(x_historico), lwd=2)In [ ]: Library(plotrix)
derivada_myfunc<-function(x, h, func) { (func(x+h) - func(x))/h}
x_0 <- -20
delta <- 1
#delta <- 3 #Cambiar delta
h <- 0.001
criterio_convergencia <- 0.5
x historico<-c()x_new <- x_0 - derivada_myfunc(x_0,h,myfunc2)*delta
x_0 <- x_new
x_0
x_historico<-c(x_historico,x_0)
plot(x,y,t="l")
points (x historico, myfunc2(x_historico), col="red")
color.scale.lines (x_historico, myfunc2(x_historico), c(1,1,0), 0.c(0,1,1), colvar=1:length(x_historico), lwd=2)
-18,4085884663898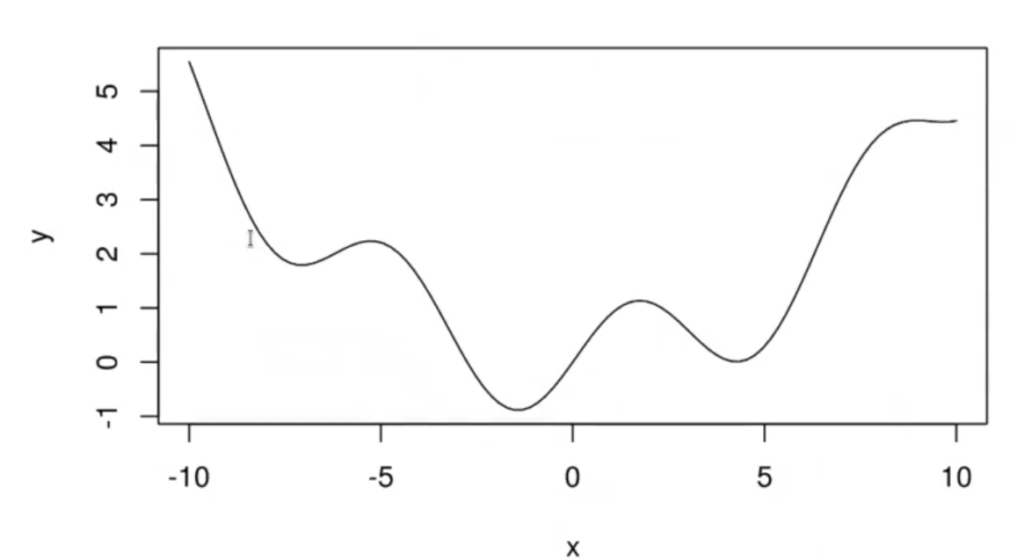
La función tiene la siguiente progresión:
- -18,4085884663898
- -17,4719052243017
- -15,91622094432
- -13,3461530005463
- -12,723005708795
- -12,4385907550803
- -12,1865650538608
- -11,8965097633672
- -11,4905062858255
- -10,8160373883828
- -9,55541778067513
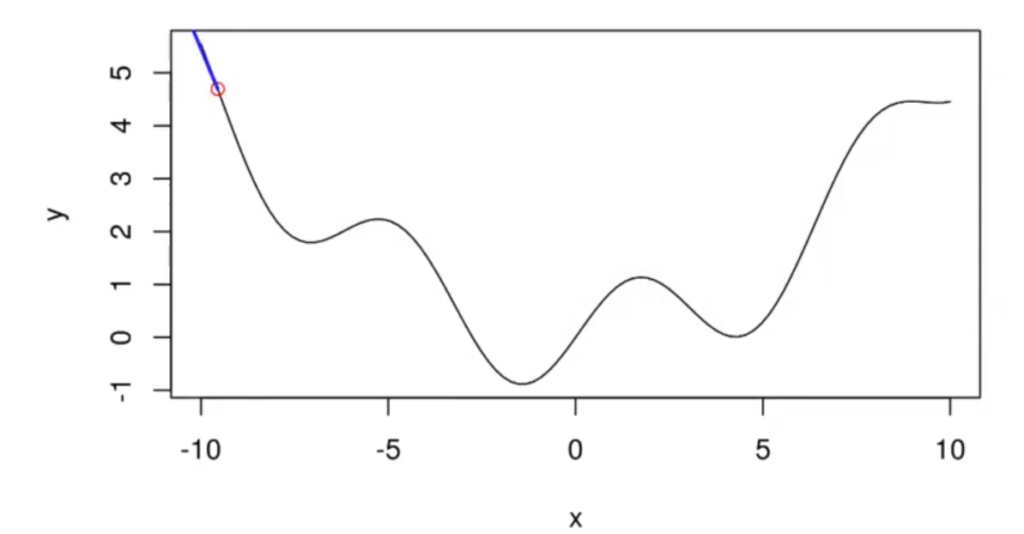
El siguiente punto se forma en este último valor.
¿Cómo va a calcular? Pues calcula la derivada, la proyecta y coloca el punto en función del delta que se haya puesto y del valor de la derivada.
- El siguiente punto sería el -7,60838228533476, expuesto en la gráfica:
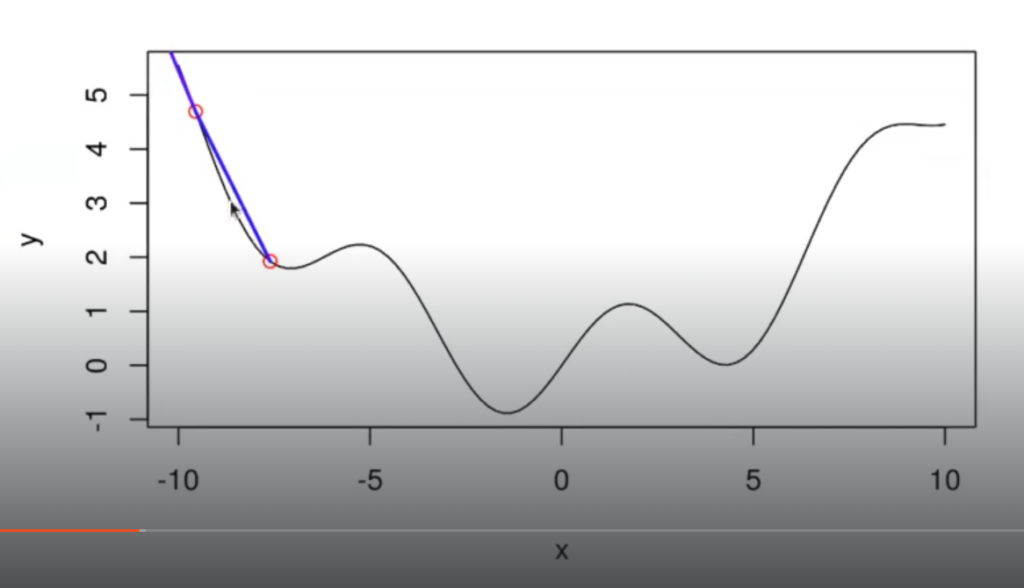
- A continuación, estaría el -7,09121674379974:
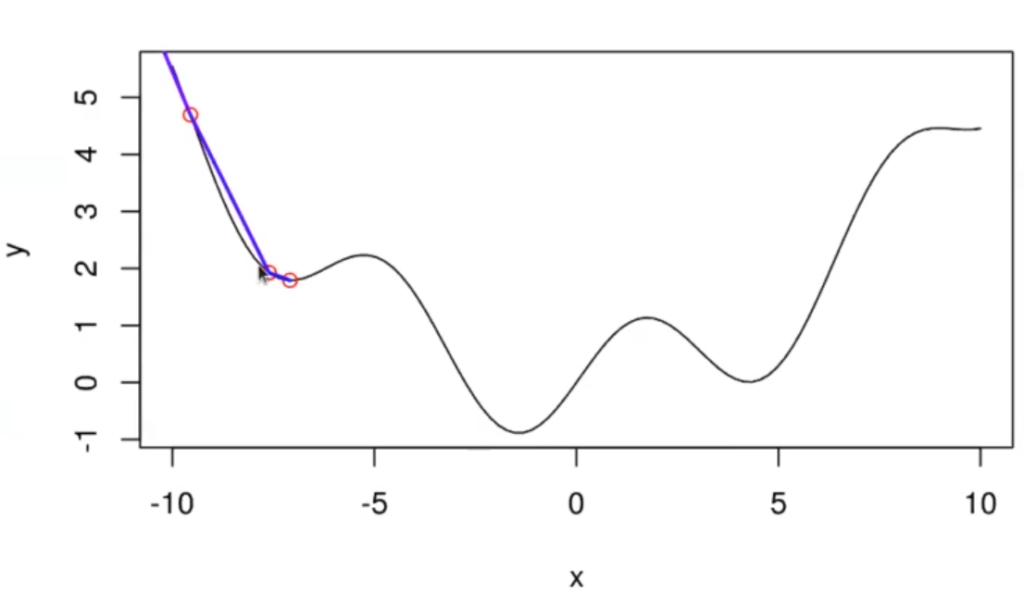
En este caso, la derivada ya sería muy pequeña. Esto se puede apreciar porque la línea se torna más horizontal que vertical.
Después de ahí, la línea no avanza más. Esto se debe a que ha convergido en un mínimo local. Después de esto, poco se puede hacer. Podríamos volver a ejecutarlo de dos formas:
- O bien cambiándole el x_0 y poniéndole otro valor.
- O bien podríamos intentar cambiar el delta.
Si le cambiamos el delta, el código quedaría así:
In [ ]: Library(plotrix)
derivada_myfunc<-function(x, h, func) { (func(x+h) - func(x))/h}
x_0 <- -20
delta <- 1
delta <- 3 #Cambiar delta
h <- 0.001
criterio_convergencia <- 0.5
x historico<-c()Al código anterior simplemente le quitamos el # que tenía en el segundo delta y con eso ya solucionamos el problema de manera parcial. Decimos parcial porque, aunque avanza, le cuesta encontrar el mínimo; esto sucede cuando tenemos deltas muy grandes:
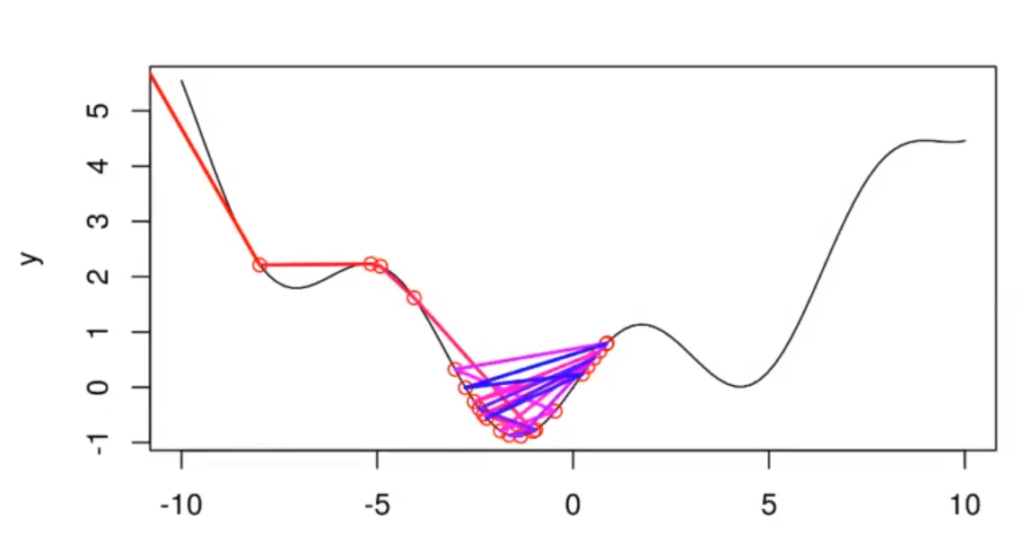
Cuando estaba atascado, el gráfico pintaba así:
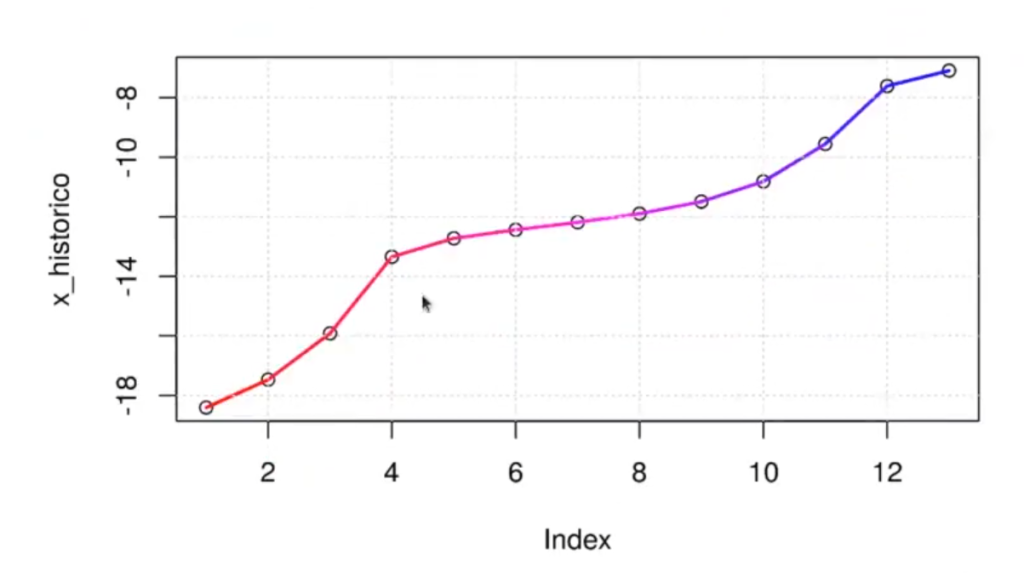
Pero cuando se cambia el delta a 3, pinta así:
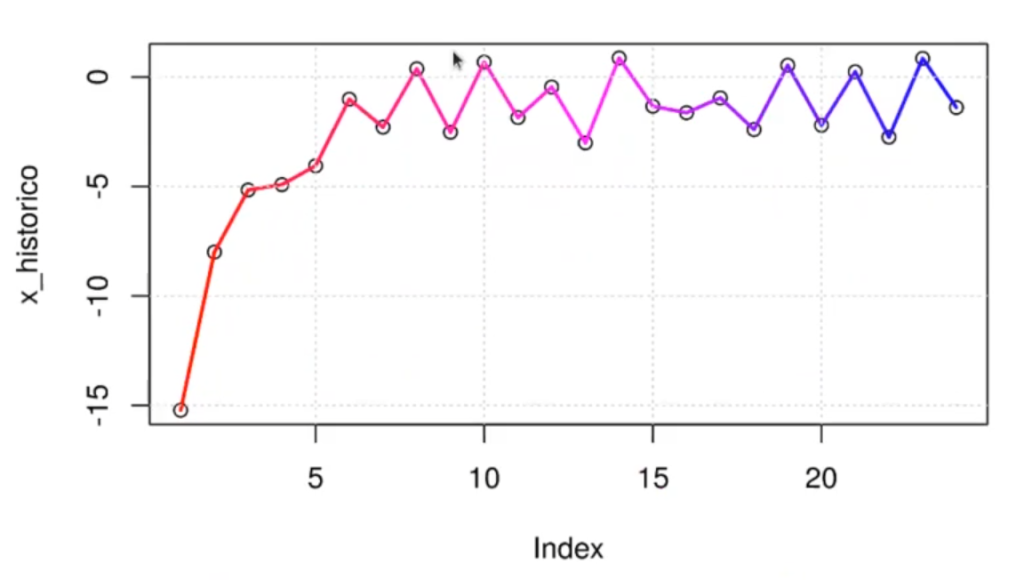
Como podemos observar, por muchas iteraciones que haga, nunca va a converger. Se ha quedado en ese punto y no hay mucho que hacer; es lo que sucede cuando tienes deltas muy grandes.
Todo está en prueba y error, por lo que debes seguir intentándolo hasta que te funcione.
¿Qué tal si, mientras sigues entendiendo de qué va esto de los mínimos en data mining, pides ayuda a los expertos? En Keepcoding tenemos para ti nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el que puedes aprender en poco tiempo todo lo necesario para incursionar en el mercado laboral. ¡Apúntate y conviértete en todo un experto!











