¿Sabías que existen distintas operaciones sobre kernels que puedes ejecutar en machine learning? En este artículo te mostraremos algunas de las operaciones sobre kernels distintos que es posible realizar, entre ellas se encuentra el entrenamiento de algoritmos.
Operaciones sobre kernels
En primera instancia, lo que haremos es entrenar un algoritmo. Esto lo haremos probando distintos kernels con diferentes valores de parámetros libres.
Primer ejercicio
#Operaciones sobre kernels: RBF
svmModel2= SVC (kernel = 'rbf', probability = True) #kernel por defecto
svmModel2.fit (x2, y2)
plot_decision_boundary_svm (x2, y2, 0.05, svmModel2)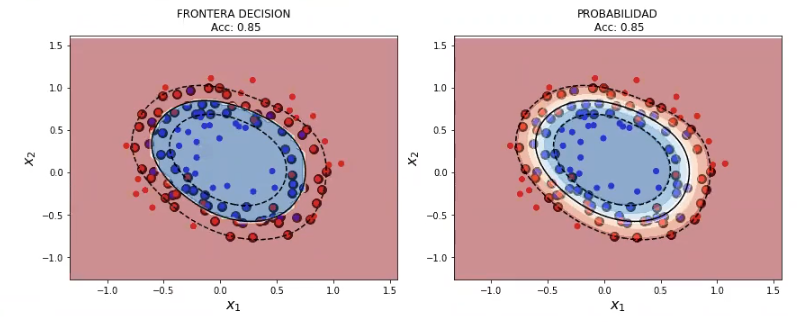
#Operaciones sobre kernels: Polinómico
svmModel2 = SVC (kernel = 'poly', degree = 2, probability = True) svmModel2.fit (x2, y2)
plot_decision_boundary_svm (x2, y2, 0.05, svmModel2)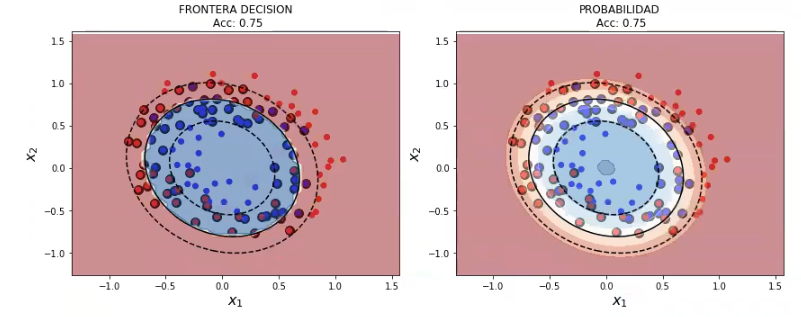
Segundo ejercicio
Lo que haremos en este segundo ejercicio es entrenar una SVM sobre un ejemplo previo.
Tenemos el modelo lineal que, como ya habíamos dicho, no sirve para generar fronteras de separación no lineal:
#Operaciones sobre kernels
#creamos el modelo
svmModel3 = SVC (kernel = 'linear', probability = True) svmModel3.fit (X3, y3)
plot_decision_boundary_svm (X3, y3, 0.05, svmModel3)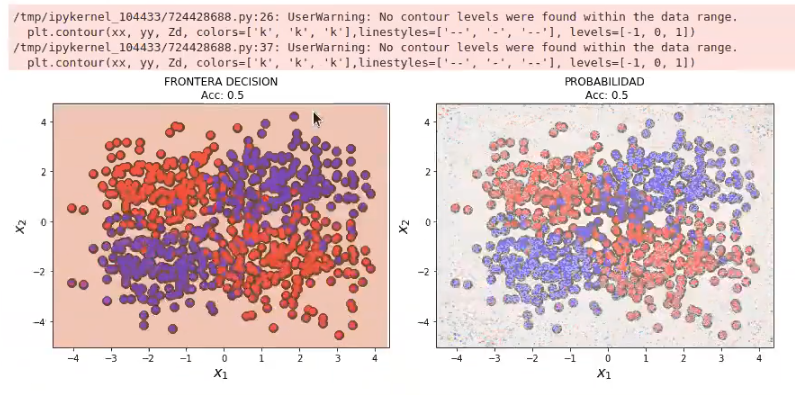
Por tanto, utilizaremos los kernels RBF y polinómico para crear esta frontera de separación. Veamos:
#Operaciones sobre kernels: RBF
svmModel3 = SVC (kernel= 'rbf', probability = True) #kernel por defecto
svmModel3.fit (X3, y3)
plot_decision_boundary_svm (X3, y3, 0.05, svmModel3)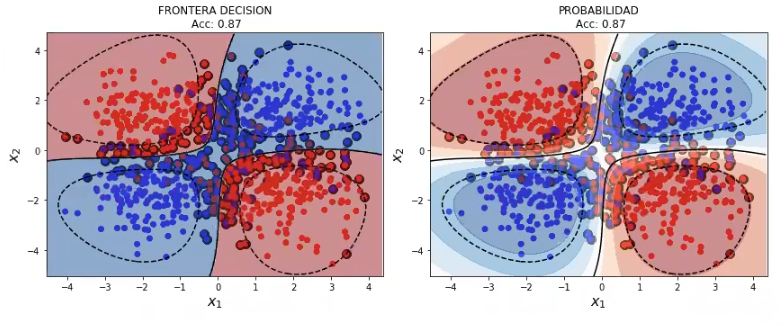
#Operaciones sobre kernels: Polinómico
svmModel3 = SVC (kernel = 'poly', degree = 4, probability = True) #kernel por defecto
svmModel3.fit (x3, y3)
plot_decision_boundary_svm (X3, y3, 0.05, svmModel3)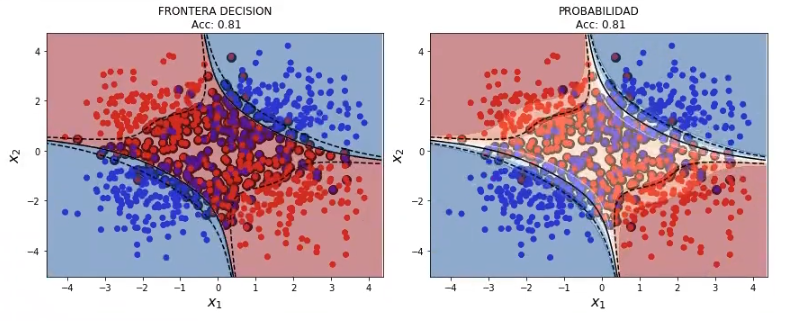
Tercer ejercicio
Suponiendo un kernel RBD calcule el valor óptimo de C y gamma para un ejemplo determinado, ¿cuáles son las prestaciones del algoritmo para este ejemplo?
#Operaciones sobre kernels
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
#Paso 1:
X_train, X_test, y_train, y_test = train_test_split (X3, y3, test_size = 0.3, shuffle = True, random_state = 0)
#Paso 2:
vectorC = np.logspace (-3, 3, 21)
vectorG = np.logspace (-5, 1, 21)
param grid= ['C': vectorc, gamma : vectorG)
grid GridSearchCV (SVC (kernel = 'rbf'), scoring = 'accuracy', param_grid = param_grid, cv = 5, verbose = 1).fit (x_train, y_train)
print ("best mean cross-validation score: { : , 3f}".format (grid.best_score_))
print ("best parameters: {}".format (grid.best_params_))
#Mostramos prestaciones en CV
scores = grid.cv_results_['mean_test_score'].reshape (len (vectorC), len (vectorG))
plt.figure (figsize = (10, 6))
plt.imshow (scores, interpolation = 'nearest', vmin = 0.6, vmax = 0.9)
plt.xlabel ('log (gamma)')
plt.ylabel ('Log(C)')
plt.colorbar ()
plt.xticks (np.arange (len (vectorG)), np.log10 (vectorG), rotation = 90)
plt.yticks (np.arange (len (vectorC)), np.log10 (vectorC))
plt.title ('5 - fold accuracy')
plt.show ()
#Paso 3: mostramos prestaciones en test
Copt = grid.best_params_ ['C']
Gopt = grid.best_params_ ['gamma']
svmModel3 = SVC (kernel = 'rbf', gamma = Gopt, C = Copt, probability = True).fit (x_train, y_train)
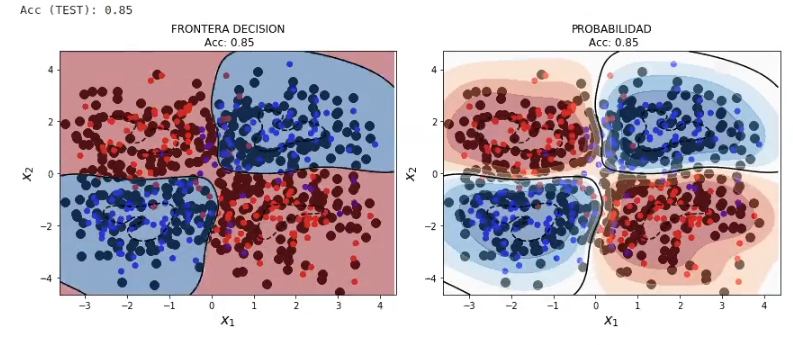
print ('Acc (TEST): %0.2f'% svmModel3.score (X_test, y_test))
plot_decision_boundary_svm (X_test, y_test, 0.05, svmModel3)Fitting 5 folds for each of 441 candidates, totalling 2205 fits
[Parallel (n_jobs = 1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel (n_jobs = 1)]: Done 2205 out of 2205 | elapsed: 12.8s finished
best mean cross – validation score: 0.870
best parameters: {‘C’: 0.0630957344480193, ‘gamma: 1.2589254117941662}
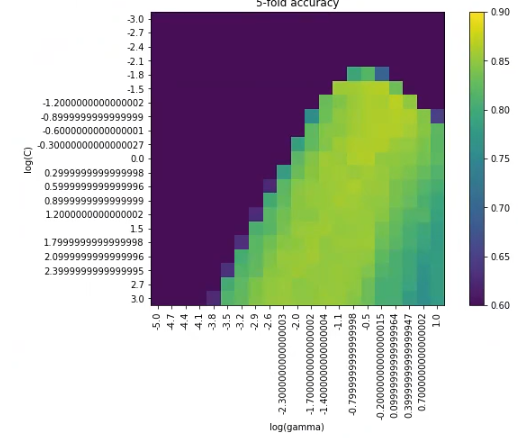
Aquí hemos aprendido también otro modo de hacer barridos con dos parámetros. Hay gente que lo ve mejor con diferentes gráficas, otros con gráficos de colores como el anterior.
¿Cuál es mejor? Pues depende. Si los barridos son sobre pocos valores (por ejemplo, 4 – 3), el de gráficos distintos sería mejor. En este caso, que son 21 los valores, hacer 21 gráficas diferentes es una locura, por lo tanto, sería más óptimo representar dichos valores por medio del gráfico de colores, porque además nos va a dar el mejor parámetro, que este caso es 0.06.
La solución a este problema es aplicarle el logaritmo:
Acc (TEST): 0.85
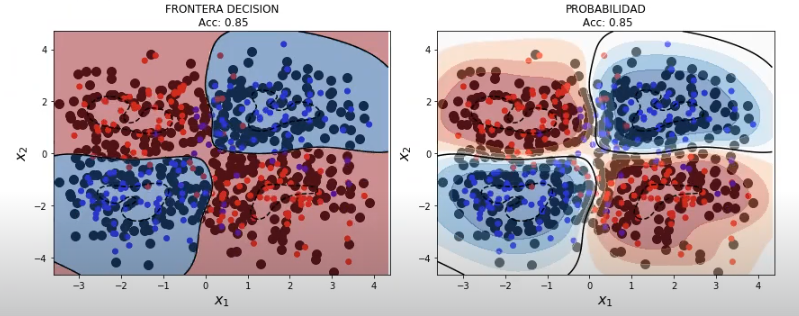
El resultado nos dice que los mejores valores son C: 0.0630957344480193 y gamma: 1.2589254117941662. Pero como tenemos nuestro ejercicio en escala logarítmica, no podemos saber de qué son esos valores, porque no los podemos reconocer en la gráfica.
#Operaciones sobre kernels
import math
#best parameters: ('C': 0.0630957344480793, gamma 1.2589254117941662)
print (f"Log (C): {math.log10 (grid.best_params_['C'])} \nLog (gamma): {math.log10 (grid.best_params_ ('gamma'])}")Este último print lo ponemos junto a los otros en la sección de código anterior, justo debajo de print params y print cross – validation. El import lo ponemos en la primera línea de código, encima del resto. El resultado sería:
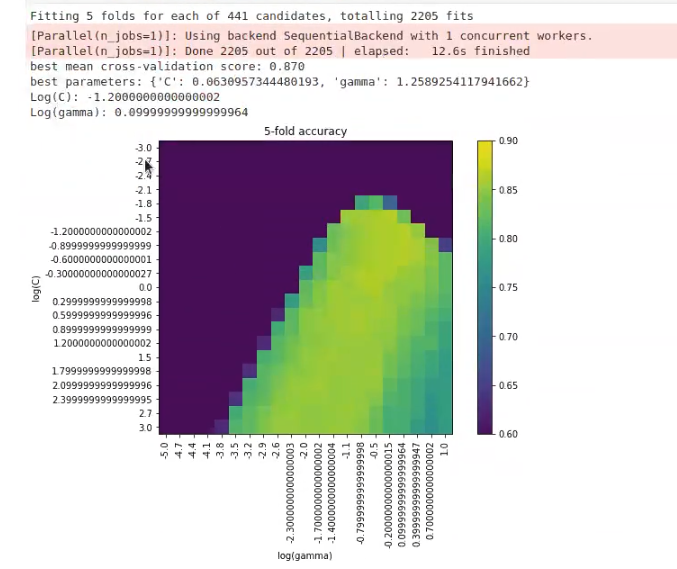
Con esto tendríamos los valores reales de c y gamma.
El Big Data es una disciplina con una amplia gama de opciones que puedes estudiar. Entre ellas está el machine learning, del que hemos hecho algunos ejercicios en este post. Si quieres seguir aprendiendo sobre estas temáticas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación de alta intensidad en la que podrás adquirir todas las herramientas teóricas y prácticas que te permitirán incursionar en un mercado laboral lleno de oportunidades. ¡No esperes más para cambiar tu futuro y solicita información ahora!











