Cuando tenemos algoritmos sesgados hacia la clase mayoritaria, podemos compensar esta situación asignando pesos distintos a los errores cometidos en cada una de las clases, a través del parámetro class_weight. En este artículo veremos cómo hacer uso de este parámetro por medio de un ejercicio.
Parámetro class_weight: ejercicio de regresión logística
Lo que haremos en este ejercicio será calcular los parámetros libres óptimos para cada clasificador. También ajustaremos un modelo con dichos parámetros y compararemos las métricas obtenidas con cada uno de ellos.
Tenemos, por tanto, un algoritmo que está sesgado hacia la clase mayoritaria, así que lo que haremos será utilizar el parámetro class_weight para asignar pesos distintos a los errores cometidos.
Además, trabajaremos con distintas métricas a la hora de optimizar los parámetros libres. Para conjuntos desbalanceados es adecuada:
‘f1’: F1 – score, compromiso entre SEN y PPV
Lo que haremos en primera instancia será ejecutar un barrido sobre C en un espacio logarítmico. En GridSearch lo que hacemos es montar una regresión logística con class weight balanced, el score de f1 y la métrica.
#Parámetro class_weight en logistic regression
from sklearn.model selection import GridSearchCV
vectorc = np.logspace (-3, 3, 21)
param_grid = {'C': vectorC}
grid = GridSearchCV (LogisticRegression (random_state = 0, class_weight = 'balanced'), scoring = 'f1', param_grid = param_grid, cv = 5)
grid.fit(Xs_train, y_train)
print ("best mean cross - validation score: {: . 3f}".format (grid.best_score_))
print ("best parameters: {}".format (grid.best_params_))
print (f "Log (C): {math.log10 (grid.best_params_ ['C'])}")
#Parámetro class_weight en logistic regression
scores = grid.cv_results ['mean_test_score')
std_scores = grid.cv results_ ['std_test_score"]
plt.errorbar (np.log10 (vectorC), scores, yerr = std_scores, fmt = ' o- ', ecolor = 'g')
plt.xlabel ('Log(C)', fontsize = 16)
plt.ylabel ('10 - Fold MSE)
plt.grid ()
plt.show ()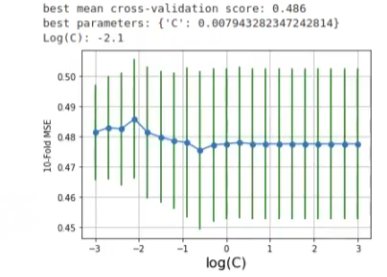
Vemos que el logaritmo de C es -2.1, es decir, el punto que le da el óptimo es el que aparece más alto en la gráfica, en este caso es -2.
#Parámetro class_weight en logistic regression
Copt = grid.best_params ['C']
lr = LogisticRegression (random_state = 0, C = Copt).fit (xs_train, y_train)
y_pred = r.predict (Xs_test)
confmat_test = confusion_matrix [y_test, y_pred)
plot_confusion_matrix (confmat_test)
calcula_metricas (confmat_test)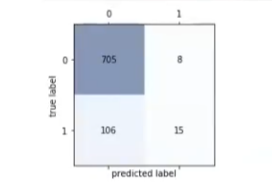
ACC: 0.8633093525179856
SEN: 0.12396694214876033
ESP: 0.9887798036465638
PPV: 0.6521739130434783
FSC: 0.20833333333333334
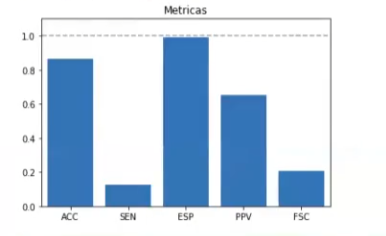
Con estos resultados podemos observar que la especificidad (ESP) es de casi 100 (0.98), pero la sensibilidad (SEN) es de 0.1. Fijémonos en las etiquetas de fuga que están correctamente clasificadas: son 15 de un total de 121.
Entonces, si pintamos el histograma, vemos que, prácticamente, no hay fugas, según nuestro modelo.
Generalmente, depende del caso de uso, pero en este en concreto el escenario será algo así como: el data scientist necesita determinar, por medio del modelo, cuántas personas se fugan, pero el algoritmo nos dirá que no se fuga nadie. Por supuesto, nosotros sabemos que esto es mentira, ya que hay mucha gente que se está yendo de las compañías debido a diferentes razones.
Sabemos que la información de que nadie se fuga es completamente falsa.
#Parámetro class_weight en logistic regression
y_prob = lr.predict_proba (Xs_test) [ : , 1]
idx_0 = (y_test == 0)
idx_1 = (y_test == 1)
plt.hist (y_prob [idx_0], density = 0, alpha = 0.75, label = 'y = 0')
plt.hist (y_prob [idx_1], density = 0, facecolor = 'red', alpha = 0.75, label = 'y = 1')
plt.legend ()
plt.title (feature)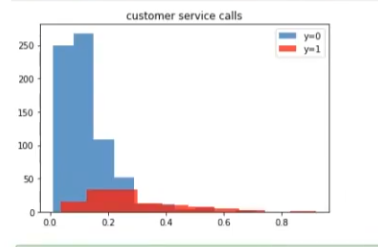
Una vez fijados los parámetros libres, representaremos la curva ROC.
#Parámetro class_weight en logistic regression
from sklearn.metrics import roc_curve, auc
ejex, ejey, = roc_curve (y_test, y_prob)
roc_auc = auc (ejex, ejey)
plt.figure ()
plt.plot (ejex, ejey, color = 'darkorange', lw = 2, label = 'AUC = %0.2f' % roc_auc)
plt.plot ([0, 1], [0, 1], color = (0.6, 0.6, 0.6), linestyle = ' - - ')
plt.plot ([0, 0, 1], [0, 1, 1], lw = 2, linestyle = ' : ', color = 'black', label = 'Clasificador perfecto')
#Parámetro class_weight en logistic regression
plt.xlim ([-0.05, 1.05])
plt.ylim ([-0.05, 1.651)
plt.xlabel ('FPR (1 - ESP))
plt.ylabel ('SEN)
plt.legend (loc = 'lower right')
plt.show ()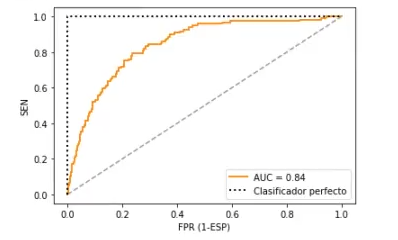
Como hemos visto, el parámetro class_weight ha tenido una gran influencia en todos aquellos problemas que estaban desbalanceados. Una de las desventajas que presenta, como ya hemos visto con otras funciones, es que la precisión se sacrifica por el bien de una mayor captura de eventos. Dependiendo de nuestra situación, la existencia de estos falsos positivos será o no será un problema.
El Big Data es una de las áreas en las que más trabajos se ofertan. Si quieres tener la posibilidad de acceder a este tipo de opciones laborales, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán obtener el trabajo de tus sueños. Además, contarás con acceso a la bolsa de talento de por vida. ¡No esperes más para seguir tu camino hacia el éxito y solicita información ahora!











