El problema de Monty Hall en estadística

El problema de Monty Hall en estadística no es más que un claro ejemplo de cómo se lleva a cabo un proceso de análisis estadístico para el manejo de los macrodatos.

En este post, te explicamos cómo el problema de Monty Hall en estadística funciona como una gran práctica para comprender este campo en el manejo del Big Data.

El problema de Monty Hall en estadística

El problema de Monty Hall en estadística recibe su nombre tras el programa de televisión Let’s Make a Deal presentado por Monty Hall en la década de 1970. El enunciado más famoso del problema, extraído de Parade Magazine en 1990:

Supón que estás en un concurso y se te ofrece escoger entre tres puertas: detrás de una de ellas hay un coche y detrás de las otras, cabras. Escoges una puerta, digamos la nº1, y el presentador, que sabe lo que hay detrás de las puertas, abre otra, digamos la nº3, que contiene una cabra. Entonces te pregunta: “¿No prefieres escoger la nº2?”. ¿Es mejor para ti cambiar tu elección?

Hay tres hipótesis:

• H1: el coche está tras la puerta 1.
• H2: el coche está tras la puerta 2.
• H3: el coche está tras la puerta 3.

Evidentemente, como no tienes ningún tipo de información adicional:

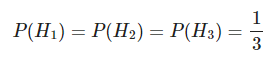
La evidencia vendrá de Monty abriendo una puerta, evidentemente sabrás que:

• Monty siempre abrirá una puerta de las 2 que no hayamos seleccionado.
• Monty nunca abrirá la puerta que tenga el coche.

Interesado en la probabilidad de que el coche esté detrás de una puerta utilizando nuestro conocimiento: imagina que el concursante selecciona la puerta 1, a continuación Monty selecciona la puerta 3. Las siguientes probabilidades condicionales ocurren:

• Condición, el coche está tras la puerta 1: puede abrir igualmente la puerta 2 o 3.

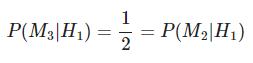
• Condición, el coche está tras la puerta 2: puede abrir solo la puerta 3.

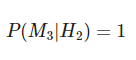
• Condición, el coche está tras la puerta 3: no podría abrir esa puerta.

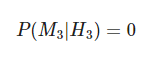
Desde este punto de vista, la probabilidad marginal de que Monty elija la puerta 2 o 3 es la misma, porque no sabes dónde está el coche. Solo sabes que nunca elegirá la puerta 1, porque es la que seleccionó el concursante:

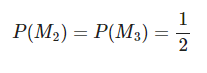
Ahora hay dos opciones, cambiar a la puerta 2 o mantenerse en la puerta 1.

• Se mantiene en puerta 1, sabiendo que la puerta 3 no tiene premio:

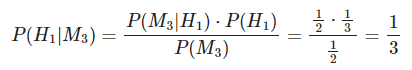
• Se cambia a la puerta 2, sabiendo que la puerta 3 no tiene premio:

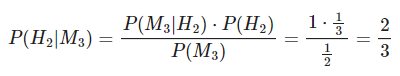
Así, se ve que la probabilidad de cambiar de puerta es 2/3, mientras que la probabilidad de mantenerse con la original es 1/3.

N<-10000
puerta_con_premio<-floor(runif(N,min=1,max=4))

seleccion_inicial_del_concursante<-floor(runif(N,min=1,max=4))
seleccion_cambiada_del_concursante<-rep(NA,N)

for (i in 1:N){
    
    # Monty selecciona una puerta
    if (puerta_con_premio[i]==1){
        if (puerta_con_premio[i]==seleccion_inicial_del_concursante[i]){
            seleccion_monty<-ifelse(runif(1)>0.5,2,3)
        }else{
            seleccion_monty<-ifelse(seleccion_inicial_del_concursante[i]==3,2,3)
        }
    }else if (puerta_con_premio[i]==2){
        if (puerta_con_premio[i]==seleccion_inicial_del_concursante[i]){
            seleccion_monty<-ifelse(runif(1)>0.5,1,3)
        }else{
            seleccion_monty<-ifelse(seleccion_inicial_del_concursante[i]==3,1,3)
        }        
    }else if (puerta_con_premio[i]==3){
        if (puerta_con_premio[i]==seleccion_inicial_del_concursante[i]){
            seleccion_monty<-ifelse(runif(1)>0.5,1,2)
        }else{
            seleccion_monty<-ifelse(seleccion_inicial_del_concursante[i]==1,2,1)
        }
    }
    
    # El concursante selecciona otra puerta
    puertas_prohibidas<-c(seleccion_monty,seleccion_inicial_del_concursante[i])
    seleccion_cambiada_del_concursante[i]<-which(is.na(match(1:3,puertas_prohibidas)))    
}

p1<-mean(seleccion_inicial_del_concursante==puerta_con_premio)
print(paste0("Si el concursante nunca cambia de puerta la probabilidad de acertar es:",p1))
p2<-mean(seleccion_cambiada_del_concursante==puerta_con_premio)
print(paste0("Si el concursante siempre cambia de puerta la probabilidad de acertar es:",p2))

Has aprendido qué es el problema de Monty Hall en estadística; no obstante, sabemos que todavía queda mucho más por aprender de este campo. Por ello, te presentamos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, una formación intensiva que te permitirá convertirte en un experto del sector IT.

En él aprenderás acerca del proceso de ingesta, clasificación, resguardo, procesamiento y presentación de los datos utilizando diferentes herramientas. ¡Infórmate y empieza ahora!