En 1936, Fisher formuló su teoría para el análisis discriminante lineal (Lineal Discriminant Analysis LDA), que tiene muchas utilidades como clasificador.
Su concepto es similar al del PCA, en el que se trata de realizar una reducción de similaridad. No obstante, mientras el PCA es un aprendizaje no supervisado, el LDA pertenece al aprendizaje supervisado.
Ejercicio aplicando análisis discriminante lineal
Con esta información buscaremos la proyección que mejor nos permita separar las dos clases de interés, que son el LDA y el PCA.
#análisis discriminante lineal, pte 1 options (repr.plot.height = 4, repr.plot.width = 6, repr.plot.res = 300) set.seed (123) N <- 100 x1 <- rnorm (N, mean = 0, sd = 1.5) x2 <- x1 * 2 + rnorm (N, mean = 0, sd = 1) dfa <- data.frame (group = "A", x1 = x1, x2 = x2, stringsAsFactors = T) x1 <- rnorm (N, mean = 1.5, sd = 1) x2 <- x1 * 2 + rnorm (N, mean = 4, sd = 2) dfb <- data.frame (group = "B", x1 = x1, x2 = x2, stringsAsFactors = T) df <- data.frame (rbind (dfa.dfb)) options (repr.plot.height = 4, repr.plot.width = 8) library (ggplot2) ggplot (df, aes (x = x1, y = x2, color=group)) + geom_point (size = 0.1)
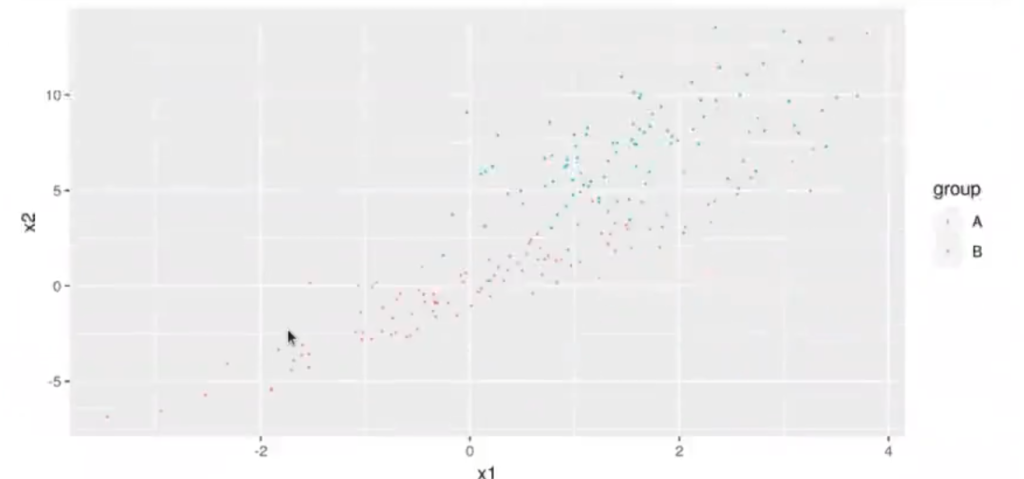
Imaginemos esta nube de puntos, donde tenemos dos grupos: el grupo A y el grupo B. Queremos encontrar una línea en la que, si queremos proyectar nuestros datos, nos los divida muy bien y haya una distribución normal.
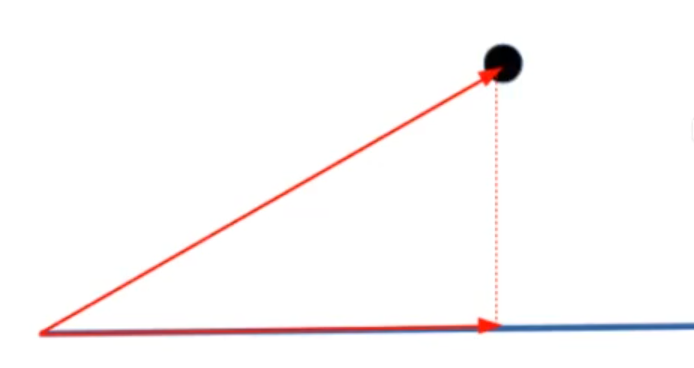
¿Qué es proyectar? Proyectar significa tomar dos vectores. Tomamos un vector por otro, hacemos el producto escalar y eso nos da una magnitud denominada proyección, es decir, la proyección de uno sobre otro. En la siguiente imagen la proyección está dada por la línea roja vertical punteada.
¿Cómo lo hacemos? Aquí te mostraremos una manera de calcular el análisis discriminante lineal.
Pintamos un vector (representado por la letra w) y ese vector es 0 en x y 1 en y, es decir, el vector va a apuntar verticalmente (como se muestra en la figura 3).
#análisis discriminante lineal, pt 2
w <- matrix (c (0.001, 1), nrow = 2)
w <- w / sqrt (sum (w ^ 2))
w
##análisis discriminante lineal, pt 3
g1 <- ggplot (df, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.1) + geom_abline (slope = w [2] / w [1])
df$projection <- as.matrix (df [ , 2 : 3]) %*% w
g2 <- ggplot (df, aes (x = projection, color = group)) + geom_density ()
library (ggpubr)
ggarrange (g1, g2, ncol = 2)
library (ROCR)
pr <- prediction (df$projection, df$group)
prf_auc = performance (pr, measure = "auc")
paste ("The AUC is", prf [email protected] [[1]])
0.0009999995 [x]
0.9999995000 [y]
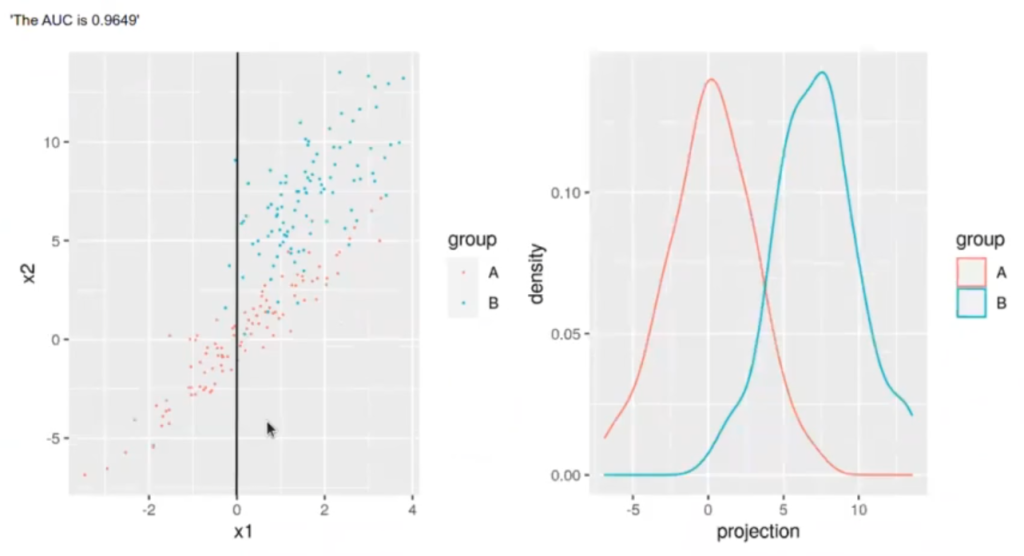
¿Qué estamos viendo en la parte derecha? Esta corresponde a la proyección de todos los puntos sobre esa línea. Si hacemos todos los puntos de la recta y los pintamos en una gráfica de distribución, lo que se obtiene es la imagen que se presenta en la derecha.
Posterior a esto, crearemos un dataframe que será la proyección de nuestros datos en las columnas 2 y 3. Ese dataframe lo multiplicamos por el vector w, lo que nos dará un valor.
Ahora, ¿qué tal si en vez de hacer esto: w <- matrix (c (0.001, 1), nrow = 2), hacemos esto: w <- matrix (c (1, 1), nrow = 2)?
Esto nos da una curva de separación. Es como una salida de proyección de una regresión logística, que nos está dando valores entre positivos y negativos.
Esta predicción nos permite calcular un umbral y decir la calidad de la misma. En función de dónde coloquemos el umbral, lo que está a un lado del umbral será a y lo que está al otro lado será b.
¿Qué pasa, entonces, con los puntos cruzados? Si, por ejemplo, ponemos el umbral en la mitad de las dos líneas de la gráfica de distribución, algunos puntos de la recta se tomarían como errores:
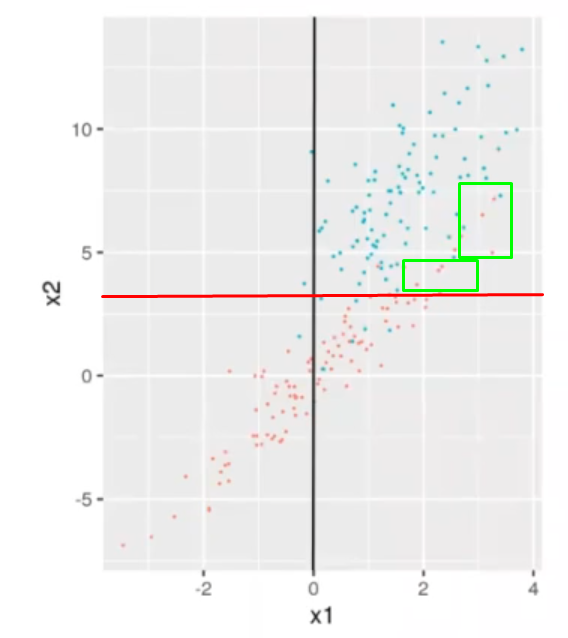
Los puntos rojos señalados dentro del cuadro verde se tomarían como errores, ya que están fuera del umbral. Pasa lo mismo con los puntos azules que están en la parte de abajo del umbral, también serían considerados como errores.
Con esto ya tendríamos calculado el análisis discriminante lineal.
Si te ha gustado aprender sobre el análisis discriminante lineal y quieres seguir ampliando tus conocimientos, recuerda que puedes seguir nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva de 8 meses de duración en la cual podrás adquirir todos los conocimientos necesarios para incursionar en uno de los mercados laborales más prolíficos y con mejores ofertas de empleo. Recuerda que tenemos a los mejores profesionales para acompañarte durante todo tu proceso y que puedas seguir forjando tu futuro y construyendo tus sueños. ¡Anímate y solicita más información!











