¿Qué es el gradient descent?

Los least squares o mínimos cuadrados nos permite encontrar la recta que mejor aproxima nuestros datos. Los métodos que nos permiten encontrar la solución mínima o máxima se llaman métodos de optimización. Existen numerosos tipos de métodos de optimización, pero, en este post, nos vamos a centrar en uno de los más usados hoy en día en el mundo del machine learning: el gradient descent o gradiente descendente.

¿Qué es el gradient descent?

El gradient descent es un método de optimización iterativo (cada iteración que ejecutamos estamos un poco más cerca del mínimo de la función-solución).

Lo que queremos hacer es calcular la solución de la siguiente función:

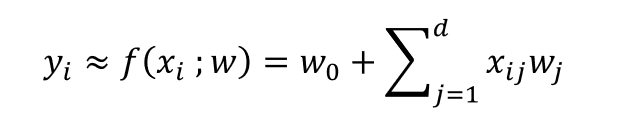
Los valores que deberán hallarse son los de w₀ y de w₁, w₂, w₃… w_n.

Podemos convertirlo en matrices:

y_i ≈ f (x_i ; w) = XW

Y queremos encontrar:

• Los argumentos w que minimizan la función argmin f (w).

Nota: min f (x) y arg min f (x) son cosas distintas. Por ejemplo:

Considera la función f (x) = 100 + (x – 3)²

min f (x) = f (arg min f (x))

Entonces:

d f (x) / x = 2 (x – 3)

arg min 2 (x – 3) = 0

arg min f (x) = 3

Por otro lado:

min f (x) = f (arg min f (x)) = 100 + (3 – 3)²

min f (x) = 100

El gradient descent no es igual que los mínimos cuadrados, donde simplemente se debe aplicar la fórmula y nos muestra los resultados de un tirón.

Este es un método iterativo, por tanto, cada vez que ejecutamos una iteración del gradient descent, vamos a estar un poquito más cerca de la solución. Si en la primera iteración estamos en un punto alejado, lo que debemos hacer es ejecutar otra iteración, en la que estaremos un poco más cerca del resultado. Así, sucesivamente, con cada iteración vamos llegando al resultado que esperamos, es decir, a la solución final. Por esta razón decimos que es un método de optimización iterativo.

Podemos graficar este proceso de optimización. Como siempre, utilizaremos matplotlib y numpy.

#gradient descent
import matplotlib.pyplot as plt
import numpy as np

fig, axs = plt.subplots ()

x = np.linspace (-5, 5, 100)

#Calculate the y value for each element of the x vector
y = 100 + (x - 3) ** 2

axs.annotate ('arg min f (x)',
                         xy = 0.05, 0), xycoords = 'axes fraction',
                         xytest = (-0, 0), textcoords = 'offset pixels',
                         horizontalaligment = 'right',
                         verticalaligment = 'bottom',
                         color = 'r'

axs.annotate ('min f (x)',
                         xy = 0, 0.1), xycoords = 'axes fraction',
                         xytest = (-0, 0), textcoords = 'offset pixels',
                         horizontalaligment = 'right',
                         verticalaligment = 'bottom',
                         color = 'r'

axs.plot (x, y)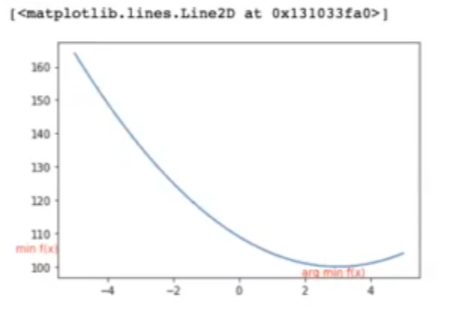

El arg min

Para entender cómo funciona el gradient descent, es necesario que comprendamos la función que cumple el arg min dentro de todo este proceso.

Tenemos, pues, una función que depende de w (f (w)) y queremos encontrar los parámetros que hacen mínima a esta función. Entonces, como podemos observar en la graficación del resultado del gradient descent, tenemos una curva. El valor que hace mínima la función, que es lo que queremos encontrar, está en la parte inferior, señalado en rojo:

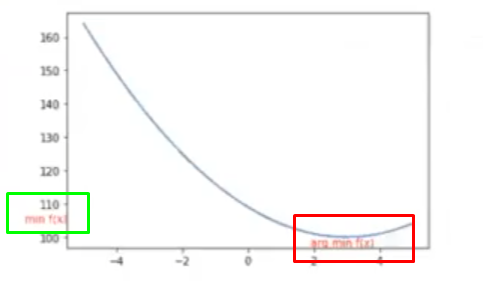
El mínimo de la función está en el eje y, señalado en verde. Entonces, cabe preguntarse: ¿cuál es el valor de x que nos permite obtener el mínimo de la función?

Sabemos que el mínimo de esta función es 100. Asimismo, el valor de x que tenemos que evaluar para que nos dé 100 es 3.

Como queremos encontrar el valor de w que hace mínimo f (x), es decir, arg min f (x), los pasos a seguir son:

• Empezar en algún punto aleatorio de la curva.
• Iterativamente, movernos en la dirección de mayor pendiente ∇ f (x) con pasos con tamaño n.

x : = x – n . ∇ f (x)

x_i = x_i-1 – n . ∇ f (x)

El parámetro n se denomina learning rate y es el parámetro que se encarga de medir el step size en cada iteración mientras nos movemos hacia el mínimo de la función.

¿Quieres seguir avanzando en tu formación profesional?

Ahora que ya has visto cómo funciona el gradient descent, puedes seguir avanzando en tu proceso formativo. Big Data es una de las áreas en las que más trabajos se ofertan. Para poder acceder a este tipo de opciones laborales, unas de las más prolíficas y mejor pagadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán entrar en el mercado laboral. ¡No esperes más para impulsar tu carrera y solicita información ahora!