El álgebra puede parecer un mundo complicado lleno de letras y números, pero en realidad es una forma poderosa de comunicarse y resolver problemas matemáticos. En este artículo, vamos a explorar qué es el lenguaje algebraico, cómo se usan las expresiones algebraicas y por qué son tan importantes. ¡Prepárate para descubrir el fascinante mundo del lenguaje del álgebra!
¿Qué es el lenguaje algebraico?
El lenguaje algebraico es una forma de comunicación matemática que utiliza símbolos y letras para representar relaciones y operaciones entre cantidades desconocidas. Estas cantidades desconocidas se llaman variables y son fundamentales en el lenguaje algebraico. Este lenguaje nos permite describir situaciones matemáticas de manera compacta y eficiente, facilitando la resolución de problemas complejos.
Por ejemplo, la expresión:
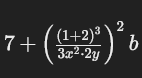
se puede leer como:
La suma de siete más el cuadrado del cociente del cubo de la suma de uno más dos entre el producto de tres equis al cuadrado por dos ye.
Importancia del lenguaje algebraico
El lenguaje algebraico es esencial en las matemáticas y tiene numerosas aplicaciones en campos como la física, la ingeniería, la economía y la informática. A través del uso del lenguaje del álgebra, podemos modelar y resolver problemas del mundo real de una manera más eficiente y precisa.
Además, el lenguaje algebraico nos permite desarrollar habilidades de razonamiento lógico y crítico, que son valiosas en muchas áreas de la vida.
Reglas del lenguaje algebraico
Para usar el lenguaje algebraico de manera correcta, es importante seguir ciertas reglas:
- Cada operación combinada en varias etapas tiene que estar precedida del símbolo igual «=».
- Si el símbolo «=» está seguido por una raya de fracción, esta debe aparecer a una altura intermedia entre las dos rayas del igual.
- El número 1 puede omitirse cuando está multiplicando a otro número o cuando actúa como exponente.
- El símbolo de la multiplicación puede omitirse cuando a continuación del mismo aparecen unos paréntesis, o cuando se indica el producto de dos variables (letras).
¿Qué es una expresión algebraica?
Una expresión algebraica es una combinación de números, letras y símbolos de operaciones matemáticas, que respeta las reglas del lenguaje algebraico. Por ejemplo, algunas de las expresiones algebraicas más comunes son:
- n + 1se lee «el sucesor de n»
- n − 1 se lee «el antecesor de n»
- 2n se lee «entero siempre PAR»
- 2n + 1 y 2n – 1 se leen «entero siempre IMPAR»
- 2n y 2n + 2 se leen «2 pares consecutivos»
- 2n + 1 y 2n + 3 se leen «2 impares consecutivos»
- n2 se lee «cuadrado perfecto de n»
Ejemplos de expresiones algebraicas
Suma de términos
Una expresión algebraica puede ser tan simple como la suma de dos términos. Por ejemplo:
3x + 5y
En esta expresión algebraica, tenemos dos términos: 3x y 5y. La x y la y son variables, mientras que 3 y 5 son coeficientes.
Multiplicación de términos
Las expresiones algebraicas también pueden involucrar la multiplicación de términos. Considera el siguiente ejemplo:
2xy
Aquí, 2 es el coeficiente, y x e y son variables. Podemos multiplicar el coeficiente por las variables para obtener el resultado, que en este caso sería 2xy.
Potencias y exponentes
Las potencias y exponentes también son comunes en las expresiones algebraicas. Veamos un ejemplo:
(x + y)2
En esta expresión algebraica, (x + y) se eleva al exponente 2. Esto significa que debemos multiplicar (x+y) por sí mismo. Simplificando la expresión, obtenemos:
x2 + 2xy + y2
Aquí, hemos aplicado la propiedad distributiva y hemos resuelto los términos.
Importancia del lenguaje algebraico
El lenguaje algebraico es esencial en las matemáticas y tiene numerosas aplicaciones en diferentes campos:
- Física: Utiliza expresiones algebraicas para describir leyes y principios fundamentales, como la ley de la gravitación universal o las ecuaciones de movimiento.
- Ingeniería: Los ingenieros emplean el lenguaje del álgebra para diseñar estructuras, circuitos y sistemas eficientes y seguros.
- Economía: Las expresiones algebraicas permiten modelar comportamientos económicos y realizar predicciones precisas.
- Informática: Los algoritmos y las estructuras de datos a menudo se describen utilizando lenguaje algebraico para optimizar su funcionamiento.
Cómo entender las expresiones algebraicas
Entender las expresiones algebraicas puede parecer desafiante al principio, pero con práctica y algunos trucos, se vuelve más sencillo. Aquí tienes algunos consejos:
- Identifica las variables: Las letras en una expresión algebraica representan cantidades desconocidas. Identificarlas te ayudará a comprender el problema.
- Sigue las reglas del lenguaje algebraico: Asegúrate de seguir las reglas de operación y simplificación.
- Practica la simplificación: La simplificación de expresiones algebraicas es clave para resolver problemas. Practica combinando términos similares y utilizando propiedades algebraicas.
Regla de operaciones
Es fundamental recordar el orden de las operaciones al trabajar con expresiones algebraicas. El acrónimo PEMDAS (Paréntesis, Exponentes, Multiplicación y División, Adición y Sustracción) te ayudará a recordar el orden correcto.
El lenguaje algebraico es una herramienta poderosa y esencial en las matemáticas y en muchas otras disciplinas. Entender las expresiones algebraicas y cómo utilizarlas te permitirá resolver problemas complejos de manera eficiente y desarrollar habilidades de razonamiento lógico. Si quieres profundizar más en el mundo del lenguaje del álgebra y otros aspectos matemáticos, KeepCoding tiene el bootcamp perfecto para ti.
Si te apasiona la tecnología y las matemáticas, ¡KeepCoding es tu mejor opción! Nuestro bootcamp en Big data & Data science te preparan para ingresar al sector IT en tiempo récord, con habilidades demandadas y la posibilidad de cambiar tu vida. La industria tecnológica ofrece altos salarios y estabilidad laboral que otros sectores no pueden igualar. ¡No esperes más y apúntate a uno de nuestros bootcamps para iniciar tu camino hacia el éxito!











