El sistema compatible indeterminado es uno de los tres sistemas de ecuaciones que existen y, en este post, veremos en qué consiste.

Sistema compatible indeterminado

Observa el siguiente sistema de ecuaciones:

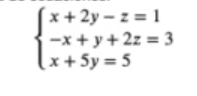
Podemos expresarlo como:

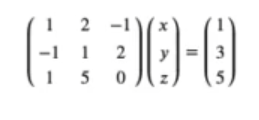
Ahora, vamos a intentar resolverlo:

#Sistema compatible indeterminado
A = np.array ([[1,  2,  -1],
                         [-1,  1,  2],
                         [1,  5,  -0]])

B = np.array ([[1],
                         [3],
                         [5]])

Lo primero es calcular el determinante de A. Si es 0, el sistema tendrá una única solución, pero si det (A) = 0, será indeterminado o no tendrá solución.

#Sistema compatible indeterminado
det_A = np.linalg-det (A)
print (det_A)

0.0

En este caso, el determinante de A es 0, por lo que hay dos opciones: tiene infinitas soluciones o no tiene solución ¿Qué podemos hacer para averiguarlo?

Vamos a aplicar el método de eliminación de Gauss para ver si podemos encontrar un sistema equivalente. Aquí vamos a usar la matriz ampliada, por lo que a la matriz A vamos a añadirle a la derecha la matriz B:

print (A)
print (B)

[[ 1 2 -1 ]

[ -1 1 2 ]

[ 1 5 0 ]]

[[ 1 ]

[ 3 ]

[ 5 ]]

#Sistema compatible indeterminado
AB = np.concatenate ((A, B), axis = 1)
AB

array (

[[ 1, 2, -1, 1 ],

[ -1, 1, 2, 3 ],

[ 1, 5, 0, 5]])

Recordemos que el objetivo del método de Gauss es transformar un sistema en otro equivalente que tiene el mismo conjunto solución:

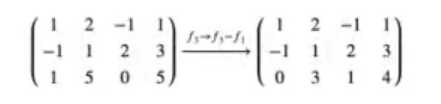
#Sistema compatible indeterminado
AB = np.array ([AB[0], AB[1], AB[2] - AB[0]])
AB

array (

[[ 1, 2, -1, 1 ],

[ -1, 1, 2, 3 ],

[ 0, 3, 1, 4 ]])

El siguiente paso que podemos hacer es:

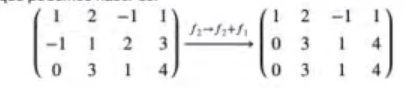
#Sistema compatible indeterminado
AB = np.array ([AB[0], AB[1], + AB[0],  AB[2]])
AB

array (

[[ 1, 2, -1, 1 ],

[ 0, 3, 1, 4 ],

[0, 3, 1, 4]])

Por último, el siguiente paso que podemos hacer es:

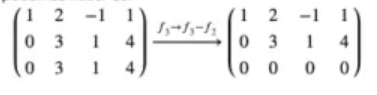
#Sistema compatible indeterminado
AB = np.array ([AB[0], AB[1], AB[2] - AB[1]])
AB

array (

[[ 1, 2, -1, 1 ],

[ 0, 3, 1, 4 ],

[0, 0, 0, 0]])

Con los pasos que hemos realizado hemos obtenido un sistema equivalente de ecuaciones al inicial, el cual podemos intentar resolver.

¿Quieres seguir aprendiendo?

Si quieres seguir aprendiendo, podrás acceder a una de las disciplinas más demandadas y con mejores sueldos de todo el mercado laboral en pocos meses con la guía del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Se trata de una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos, tanto teóricos como prácticos, para obtener el trabajo de tus sueños. ¡Entra ya para solicitar información e impulsa tu carrera!